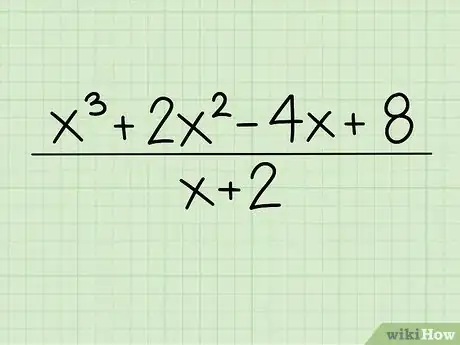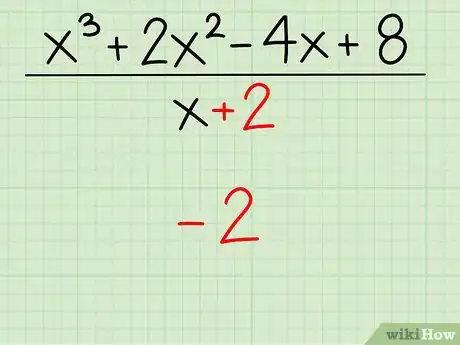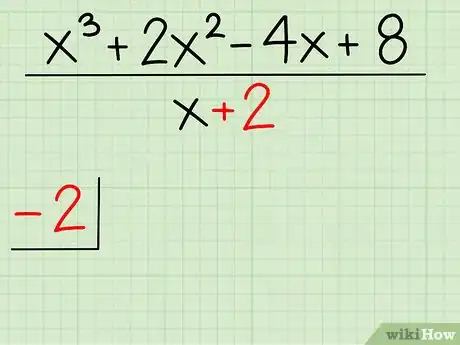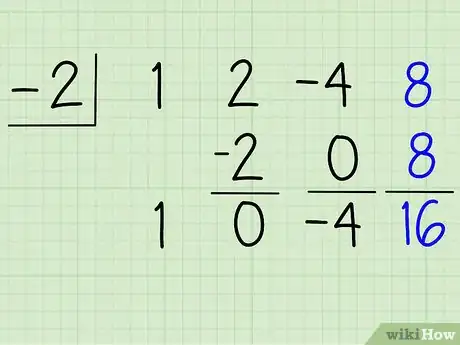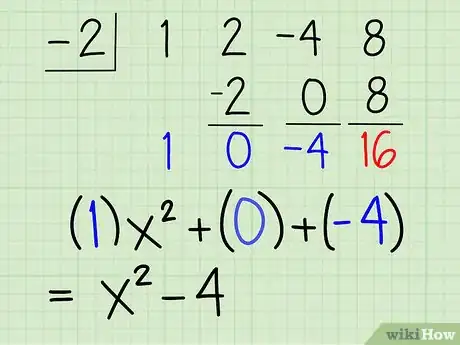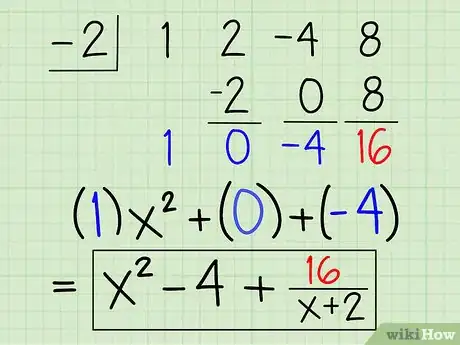Cómo dividir polinomios usando división sintética

Escribe el problema. Para este ejemplo dividiremos x³ + 2x² - 4x + 8 por x + 2. Escribe la primera ecuación polinómica, el dividendo, en el numerador y escribe la segunda ecuación, el divisor, en el denominador.

Invierte el signo de la constante en el divisor. La constante en el divisor, x + 2, es positivo 2, así que invirtiendo el signo de a constante te daría -2.

Coloca este número afuera del símbolo de división al revés. El símbolo de división al revés se verá similar a una “L” al revés. Coloca el término de -2 a la izquierda de este símbolo.

Escribe todos los coeficientes del dividendo dentro del símbolo de división. Escribe los términos de izquierda a derecha como aparecen. Debe lucir de esta manera: -2| 1 2 -4 8.

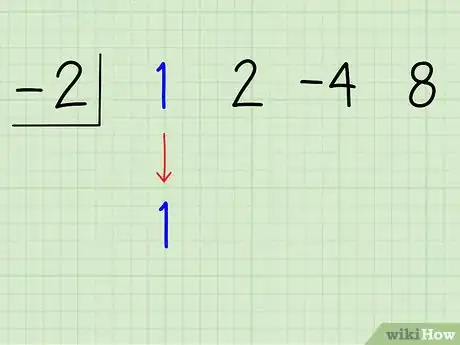
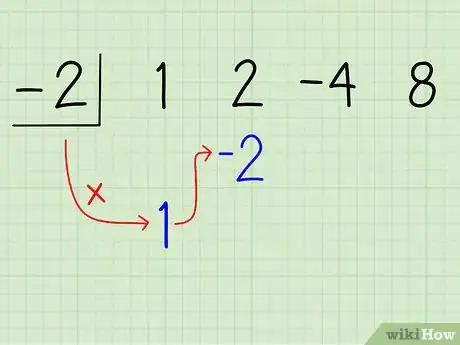
Baja el primer coeficiente. Baja el primer coeficiente, 1, debajo de sí mismo. Debe lucir de esta manera:

• -2| 1  2  -4  8
      ↓
      1

Multiplica el primer coeficiente por el divisor y colócalo debajo del segundo coeficiente. Simplemente multiplica 1 por -2 para obtener -2 y escribe este producto debajo del segundo término, 2. Así es como debería verse:

• -2| 1  2  -4  8
          -2
      1

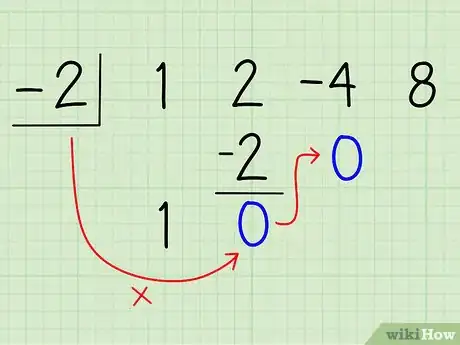
Suma el segundo coeficiente con el producto y escribe la respuesta debajo del producto. Ahora toma el segundo coeficiente, 2, y súmalo a -2. El resultado es 0. Escribe este resultado debajo de los dos números, de la misma manera que lo harías en una división larga. Así es como debería verse:

• -2| 1  2  -4  8
          -2
      1   0

Multiplica esta suma por el divisor y coloca el resultado debajo del tercer coeficiente. Ahora, toma la suma, 0, y multiplícala por el divisor, -2. El resultado es 0. Coloca este número debajo del 4, el tercer coeficiente. Así es como debería verse:

• -2| 1  2  -4  8
          -2  0 
      1   

Suma el producto con el tercer coeficiente y escribe el resultado debajo del producto. Suma 0 y -4 para obtener -4 y escribe la respuesta debajo del 0. Así es como debería verse:

• -2| 1  2  -4  8
          -2   0 
      1   0   -4

Multiplica este número por el divisor, escríbelo debajo del último coeficiente, y súmalo al coeficiente. Ahora multiplica -4 por -2 para obtener 8, escribe esta respuesta debajo del cuarto coeficiente, 8, y suma esta respuesta al cuarto coeficiente. 8 + 8 = 16, así que este es tu residuo. Escribe este número debajo del producto. Así es como debería verse:

• -2| 1  2  -4  8
          -2   0   8
      1   0   -4   |16

Coloca cada uno de los nuevos coeficientes al lado de una variable con una potencia inferior a las variables originales correspondientes. En este caso, la primera suma, 1, es colocada al lado de una x a la segunda potencia (una menos que tres). La segunda suma, 0, es colocada al lado de una x, pero el resultado es cero, así que puedes eliminar este término. Y el tercer coeficiente, -4, se convierte en una constante, un número sin variable, debido a que a variable original era x. Puedes escribir un R al lado del 16, porque es el residuo. Así es como debería verse:

• -2| 1  2  -4  8
          -2   0   8
      1   0   -4   |16
      x²   + 0x    - 4    R 16
  
  x² - 4 R16