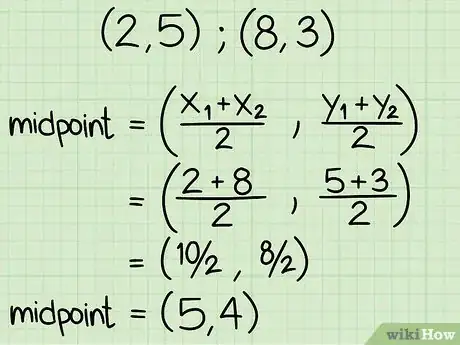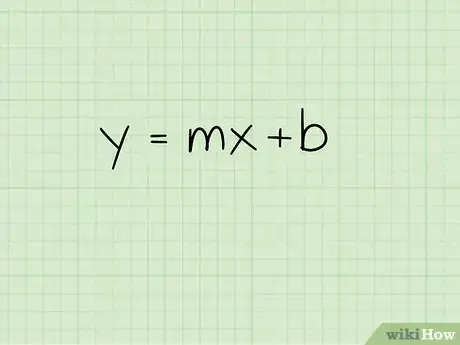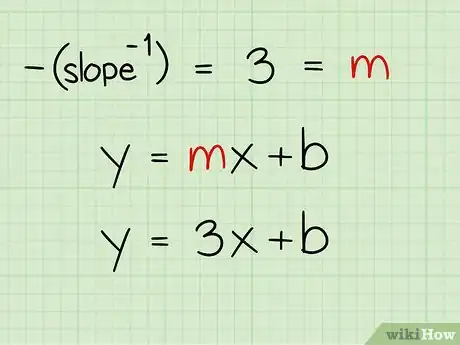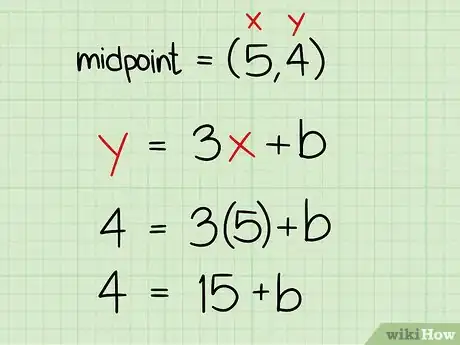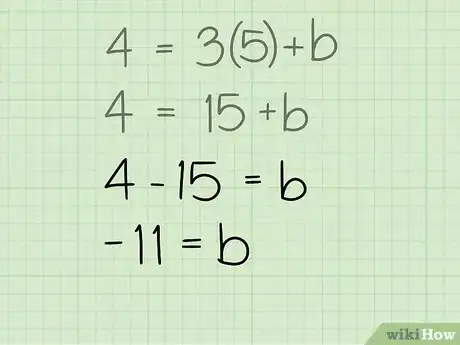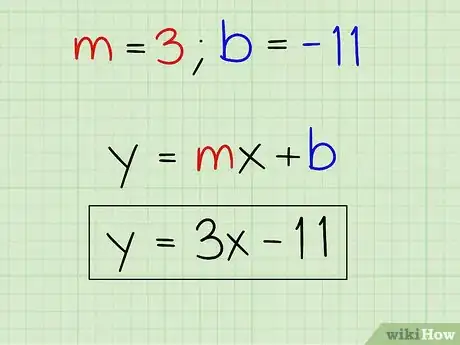Cómo encontrar el bisector perpendicular de dos puntos

Información del autor

El bisector perpendicular es una línea que corta por la mitad a un segmento de recta conectado por dos puntos, a un ángulo de 90 grados. Para encontrar el bisector perpendicular de dos puntos, todo lo que debes hacer es encontrar el punto medio y su opuesto recíproco, y colocar estas respuestas en la ecuación de la recta en su forma pendiente-ordenada. Si quieres saber cómo encontrar el bisector perpendicular de dos puntos sigue estos pasos.

Método 1

Método 1 de 2:
Junta la información necesaria

1
Encuentra el punto medio entre dos puntos. Para encontrar el punto medio, sustituye tus dos puntos en la fórmula: [(x₁ + x₂)/2,( y₁ + y₂)/2]. Esto quiere decir que estás buscando el promedio de las coordenadas x y y de los tus dos puntos, lo cual te lleva al punto medio de las dos coordenadas. Digamos que estamos trabajando con las coordenadas (x₁, y₁) de (2, 5) y las coordenadas (x₂, y₂) con los valores (8, 3). Aquí te decimos como encontrar el punto medio entre estos dos puntos:
- [(2+8)/2, (5 +3)/2] =
- (10/2, 8/2) =
- (5, 4)
- Las coordenadas del punto medio de (2, 5) y (8, 3) son (5, 4).
2
Encuentra la pendiente de dos puntos. Para encontrar la pendiente de dos puntos, simplemente sustituye en la fórmula con los valores de los puntos: (y₂ - y₁) / (x₂ - x₁). La pendiente de una línea mide la distancia de su cambio vertical entre la distancia de su cambio horizontal. Aquí verás cómo encontrar la pendiente de una línea que pasa por los puntos (2, 5) y (8, 3):
- (3-5)/(8-2) =
- -2/6 =
- -1/3
  - La pendiente de la línea es -1/3. Para encontrar esta pendiente tienes que reducir la fracción 2/6, obteniendo 1/3, debido a que tanto 2 como 6 son divisibles entre 3.
3
Encuentra el recíproco negativo de la pendiente de los dos puntos. Para encontrar el recíproco negativo de una pendiente, simplemente toma el recíproco de la pendiente y cámbiale el signo. Puedes obtener el recíproco de un número simplemente volteando las coordenadas x y y. El recíproco negativo de ½ es -2/1, o simplemente 2. El recíproco negativo de -4 es 1/4.
- El recíproco negativo de -1/3 es 3 debido a que 3/1 es el recíproco de 1/3 y el signo ha sido cambiado de negativo a positivo.
Anuncio

Método 2

Método 2 de 2:
Calcula la ecuación de la recta

1
Encuentra la ecuación de la recta en su forma pendiente-ordenada. La ecuación de una recta en su forma pendiente-ordenada es y = mx + b donde las coordenadas x y y de una recta se representan por "x" y "y," la "m" representa la pendiente de la línea y la "b" es la ordenada en el origen (el punto en el que la recta corta el eje y). Una vez que escribas esta ecuación puedes comenzar a encontrar la ecuación para el bisector perpendicular de dos puntos.
2
Coloca el recíproco negativa de la pendiente original dentro de la ecuación. El recíproco negativo de la pendiente de los puntos (2, 5) y (8, 3) dio 3. La "m" en la ecuación representa a la pendiente, así que sustituye "m" con el valor de 3 en la ecuación y = mx + b.
- 3 --> y = mx + b =
- y = 3x + b
3
Coloca los valores del punto medio en la línea. Ya sabes que el punto medio de los puntos (2, 5) y (8, 3) es (5, 4). Como el bisector perpendicular pasa por el punto medio de ambas líneas, simplemente puedes colocar las coordenadas del punto medio en la ecuación de la línea. Tan solo utiliza (5, 4) como los valores de tus coordenadas x y y.
- (5, 4) ---> y = 3x + b =
- 4 = 3(5) + b =
- 4 = 15 + b
4
Resuelve para la ordenada en el origen. Ya conoces los valores de tres de las cuatro variables de la ecuación. Ahora tienes lo que necesitas para resolver para la variable que te queda, "b", la cual es la ordenada en el origen. Simplemente despeja la variable "b" para encontrar su valor. Solo resta 15 de ambos lados de la ecuación.
- 4 = 15 + b =
- -11 = b
- b = -11
5
Escribe la ecuación de tu bisector perpendicular. Para escribir la ecuación del bisector perpendicular, solo debes sustituir con el valor de la pendiente de la línea (3) y el de la ordenada en el origen (-11) en la ecuación de la recta en la forma pendiente-ordenada. No debes utilizar ningún valor para la x y la y, debido a que esta ecuación te permitirá encontrar cualquier coordenada en la línea utilizando ya sea un valor para x o para y.
- y = mx + b
- y = 3x - 11
- La ecuación para el bisector perpendicular de los puntos (2, 5) y (8, 3) es y = 3x - 11.
Anuncio