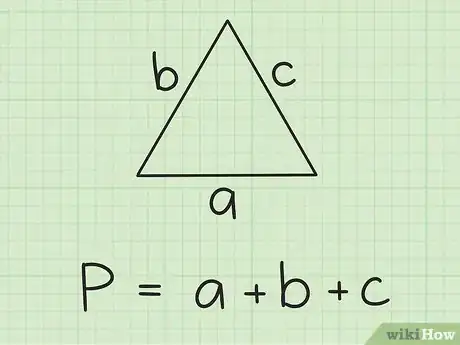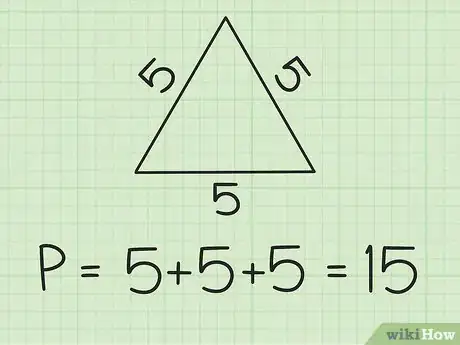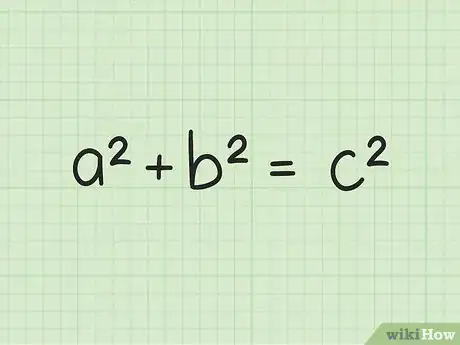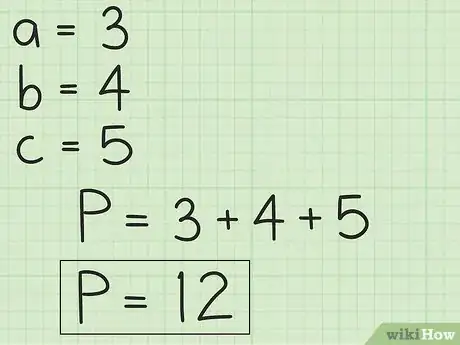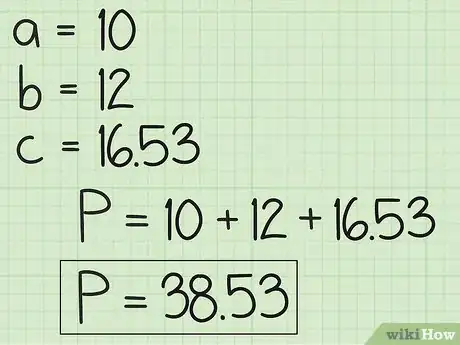Este artículo fue coescrito por Grace Imson, MA. Grace Imson es una maestra de matemáticas con más de 40 años de experiencia docente. Actualmente, Grace es instructora de matemáticas en el City College de San Francisco, y anteriormente trabajó en el Departamento de Matemáticas de la Universidad de Saint Luois. Ha enseñado matemáticas en los niveles de primaria, secundaria, preparatoria y universidad. Tiene una maestría en Educación, con una especialización en Administración y Supervisión otorgada por la Universidad de Saint Louis.
Este artículo ha sido visto 219 794 veces.
Encontrar el perímetro de un triángulo significa encontrar la distancia que hay alrededor del triángulo.[1] La forma más simple de encontrar el perímetro de un triángulo es sumar la longitud de todos sus lados, pero si no conoces las longitudes de todos los lados, primero tendrás que calcularlas. Este artículo primero te enseñará a encontrar el perímetro de un triángulo cuando conoces las longitudes de los tres lados. Esta es la forma más fácil y más común. En segundo lugar, te enseñará a encontrar el perímetro de un triángulo rectángulo cuando conoces las longitudes de dos de sus lados. Finalmente, te enseñará a encontrar el perímetro de cualquier triángulo en el cual solo conoces las longitudes de dos lados y la medida del ángulo que se forma entre ellos (un triángulo "SAS"), usando la ley de los cosenos.
Pasos
Método 1
Método 1 de 3:Hallar el perímetro si conoces las longitudes de los tres lados
-
1Recuerda la fórmula para encontrar el perímetro de un triángulo. Para un triángulo cuyos lados son a, b y c el perímetro P se define como: P = a + b + c.
- En términos más simples, lo que esta fórmula quiere decir es que, para encontrar el perímetro de un triángulo, solo debes sumar las longitudes de cada uno de sus lados.
-
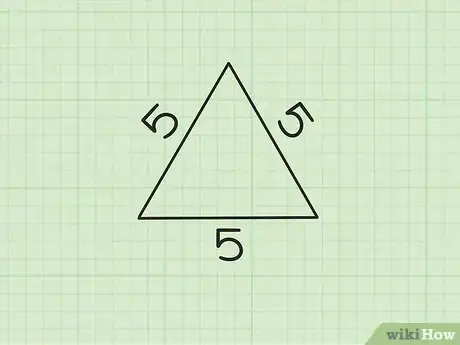
2Observa el triángulo y determina las longitudes de los tres lados. En este ejemplo, la longitud del lado a es igual a 5, la longitud del lado b es igual a 5 y la longitud del lado c es igual a 5.
- Este ejemplo en particular se conoce como triángulo equilátero, porque los tres lados tienen la misma longitud. Pero recuerda que la fórmula del perímetro es la misma para cualquier tipo de triángulo.
-
3Suma las tres longitudes de los lados para encontrar el perímetro. En este ejemplo, 5 + 5 + 5 = 15. Por lo tanto, P = 15 .
- En otro ejemplo, donde a = 4, b = 3 y c = 5, el perímetro sería: P = 3 + 4 + 5, o 12.
-
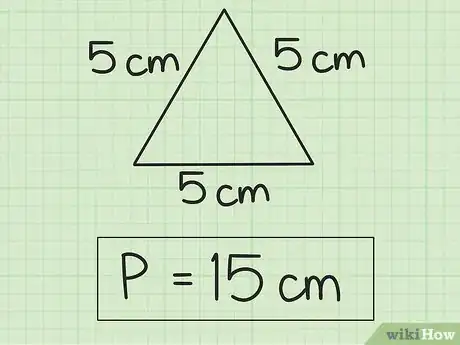
4Recuerda incluir las unidades en la respuesta final. Si los lados del triángulo se miden en centímetros, entonces tu respuesta también debe expresarse en centímetros. Si los lados se miden en términos de una variable, como x, tu respuesta también debe expresarse en términos de x.
- En este ejemplo, la longitud de los lados es 5 cm, así que el valor correcto para el perímetro es 15 cm.
Anuncio
Método 2
Método 2 de 3:Hallar el perímetro de un triángulo rectángulo si conoces la longitud de dos lados
-
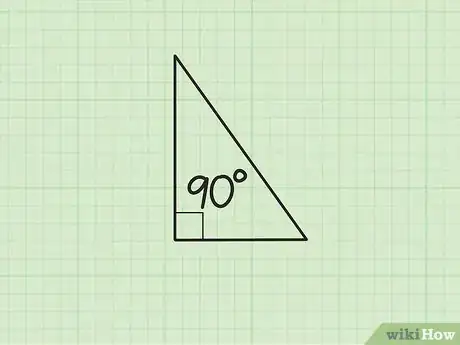
1Recuerda qué es un triángulo rectángulo. Un triángulo rectángulo es un triángulo que tiene un ángulo recto (de 90 grados). El lado del triángulo opuesto al ángulo recto siempre es el lado más largo y se conoce como "hipotenusa". Los triángulos rectángulos aparecen muy a menudo en las pruebas de matemáticas y, ¡afortunadamente existe una fórmula muy útil para encontrar la longitud de los lados desconocidos!
-
2Recuerda el teorema de Pitágoras. El teorema de Pitágoras dice que, para cualquier triángulo rectángulo cuyos lados tienen longitud a y b, y cuya hipotenusa longitud c, a2 + b2 = c2.[2]
-
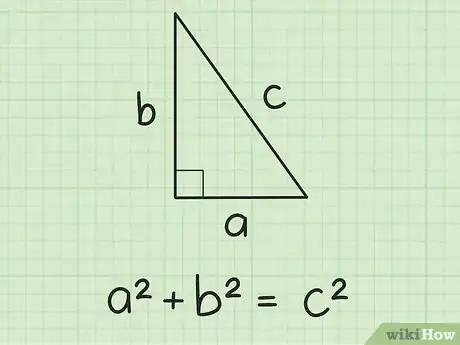
3Observa el triángulo y etiqueta los lados "a", "b" y "c". Recuerda que el lado más largo del triángulo se llama hipotenusa. Se encontrará opuesta al ángulo rectángulo y debes etiquetarla con la letra "c". Etiqueta los dos lados más cortos como "a" y "b". En realidad, no importa cuál es cual, ¡el resultado será el mismo!
-
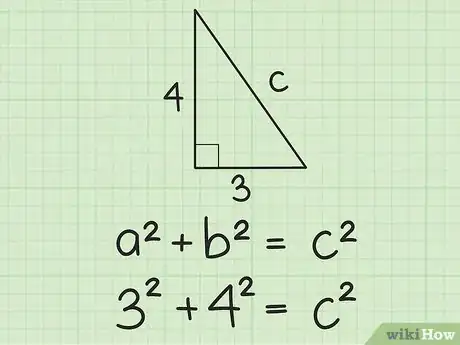
4Ingresa las longitudes de los lados en la fórmula del teorema de Pitágoras. Recuerda que a2 + b2 = c2. Sustituye las longitudes de los lados en las letras correspondientes de la ecuación.
- Si, por ejemplo, sabes que el lado a = 3 y el lado b = 4, entonces reemplaza esos valores en la fórmula de la siguiente forma: 32 + 42 = c2.
- Si sabes que la longitud del lado a = 6, y la hipotenusa c = 10, entonces debes escribir la ecuación de esta forma: 62 + b2 = 102.
-
5Resuelve la ecuación para encontrar el lado restante. En primero lugar deberás elevar al cuadrado las longitudes de los lados conocidos, lo cual significa multiplicar cada valor por sí mismo (por ejemplo, 32 = 3 * 3 = 9 ). Si quieres buscar el valor de la hipotenusa, simplemente suma los dos valores y encuentra la raíz cuadrada de este número para encontrar la longitud. Si lo que debes calcular es la longitud de uno de los lados, debes hacer una simple resta y luego calcular la raíz cuadrada para obtener la longitud de ese lado.
- En este ejemplo, eleva al cuadrado los valores en 32 + 42 = c2 para descubrir que 36 + b2 = 100. Luego, calcula la raíz cuadrada de 25 para hallar el valor de c = 5.
- En el segundo ejemplo, eleva al cuadrado los valores 62 + b2 = 102, para descubrir que 36 + b2 = 100. Resta 36 de cada lado y obtendrás b2 = 64. Luego calcula la raíz cuadrada de 64 y obtendrás el valor de b: b = 8.
-
6Suma las longitudes de los tres lados para obtener el perímetro. Recuerda que el perímetro P = a + b + c. Ahora que conoces las longitudes de los lados a, b y c, simplemente necesitas sumar las tres longitudes para encontrar el perímetro.
- En el primer ejemplo, P = 3 + 4 + 5, o 12.
- En el segundo ejemplo, P = 6 + 8 + 10, o 24.
Anuncio
Método 3
Método 3 de 3:Hallar el perímetro de un triángulo SAS usando la ley de los cosenos
-
1Aprende la ley de los cosenos. La ley de los cosenos te permite resolver cualquier triángulo cuando conoces las longitudes de dos de sus lados y la medida del ángulo que se forma entre ellos. Funciona para cualquier tipo de triángulo y es una fórmula muy útil. La ley de los cosenos establece que para cualquier triángulo con lados a, b y c, con ángulos opuestos A, B y C: c2 = a2 + b2 - 2ab cos(C).[3] [4]
-
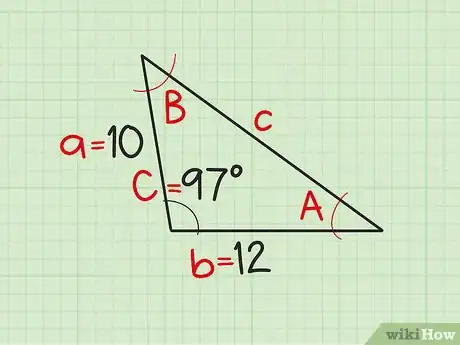
2Observa el triángulo y asígnales letras de variables a sus componentes. Debes etiquetar el primer lado conocido como a y su ángulo opuesto como A. Debes etiquetar el segundo lado conocido como b y su ángulo opuesto como B. Debes etiquetar el ángulo conocido como C y el tercer lado, el que necesitas calcular para encontrar el perímetro del triángulo, será el lado c.
- Por ejemplo, imagina un triángulo que tiene dos lados con longitudes de 10 y 12 y que el ángulo que se forma entre ellos es de 97º. Debes asignar las variables de la siguiente forma: a = 10, b = 12, C = 97°.
-
3Reemplaza los valores en la ecuación y resuélvela para obtener el lado c. En primer lugar, debes encontrar los cuadrados de a y b y sumarlos. Luego debes encontrar el coseno de C usando la función cos en tu calculadora o una calculadora de cosenos en línea.[5] Multiplica cos(C) por 2ab y restarle ese producto a la suma de a2 + b2. El resultado es c2. Encuentra la raíz cuadrada de ese valor y tendrás la longitud del lado c.Usando el triángulo del ejemplo:
- c2 = 102 + 122 - 2 × 10 × 12 × cos(97).
- c2 = 100 + 144 – (240 × -0,12187) (redondea el coseno a 5 lugares decimales).
- c2 = 244 – (-29,25)
- c2 = 244 + 29,25 (¡arrastra el símbolo menos cuando cos(C) sea negativo!)
- c2 = 273,25
- c = 16,53
-
4Usa la longitud del lado c para encontrar el perímetro del triángulo. Recuerda que el perímetro P = a + b + c, así que todo lo que necesitas hacer es sumarle la longitud que acabas de calcular para el lado c a los valores que ya tenías para el lado a y b. ¡Pan comido!
- En el ejemplo: 10 + 12 + 16,53 = 38,53, ¡que es el perímetro del triángulo!
Anuncio
Referencias
Acerca de este wikiHow
Para calcular el perímetro de un triángulo suma las longitudes de todos sus lados. Si no conoces la longitud de alguno de ellos, no podrás calcular el perímetro hasta que la encuentres. En un triángulo rectángulo, la longitud del lado faltante se puede calcular a través de la fórmula a^2 + b^2 = c^2. Esta fórmula se conoce como teorema de Pitágoras. Si vas a trabajar con un triángulo que no tiene un ángulo recto, puedes encontrar el lado faltante a través de la ley de los cosenos, que establece que c^2 = a^2 + b^2 - 2ab cos(C).