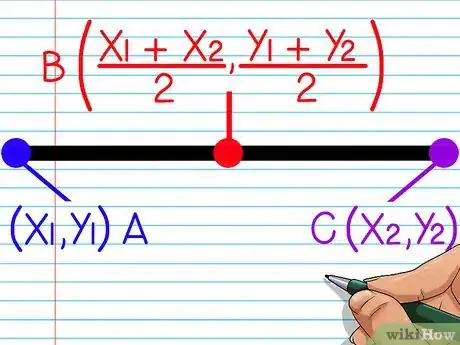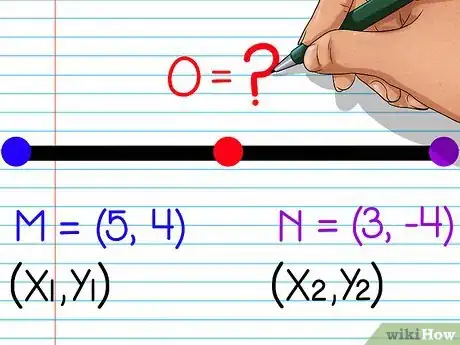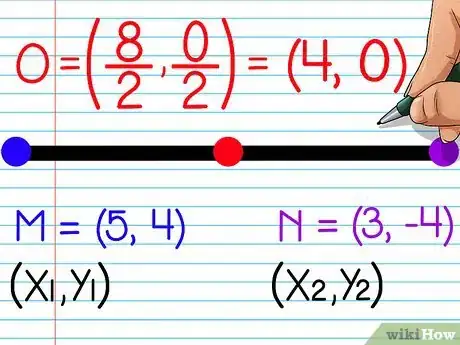Cómo encontrar el punto medio de un segmento de línea

Información del autor

Encontrar el punto medio de un segmento de recta es sencillo siempre y cuando conozcas las coordenadas de ambos extremos. La manera más común de hacer esto es utilizando la fórmula del punto medio, pero existe otra forma de encontrar el punto medio de un segmento de recta si es vertical u horizontal. Si quieres saber cómo encontrar el punto medio de un segmento de recta en unos cuantos minutos, sigue estos pasos.

Método 1

Método 1 de 2:
Utilizar la fórmula del punto medio

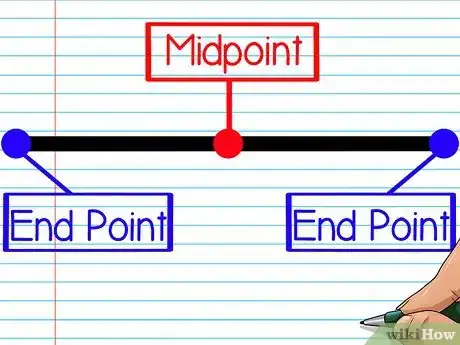
1
Entiende el punto medio. El punto medio de un segmento de recta es el punto que se encuentra localizado exactamente a la mitad de dos puntos. Se trata del promedio de ambos puntos, el cual es el promedio de las dos coordenadas x y de las dos coordenadas y.
2
Conoce la fórmula del punto medio. La fórmula del punto medio puede utilizarse al sumar las coordenadas x de los dos puntos extremos y dividiendo el resultado entre dos y luego haciendo lo mismo con las coordenadas y. Así es como se encuentra el promedio de las coordenadas x e y de los puntos extremos. Esta es la fórmula: [(x₁ + x₂)/2,( y₁ + y₂)/2]
3
Localiza las coordenadas de los puntos extremos. No puedas utilizar la fórmula del punto medio sin conocer las coordenadas x e y de los puntos extremos. Para este ejemplo queremos encontrar el punto medio, punto O, el cual se encuentra en medio de los dos puntos extremos M (5,4) y N (3,-4). Tenemos que (x₁, y₁) = (5, 4) and (x₂, y₂) = (3, -4).
- Observa que cualquiera de los dos pares de coordenadas puede servir como (x₁, y₁) o como (x₂, y₂). Ya que solo estarás sumando y dividiendo entre dos, no importa cuál par coloques primero.
4
Introduce las coordenadas correspondientes en la fórmula. Ahora que conoces las coordenadas de los puntos extremos, puedes colocarlos en la fórmula. Así es como se hace:
- [(5 + 3)/2, (4 + -4)/2]
5
Resuelve. Una vez que hayas introducido las coordenadas en la fórmula, todo lo que debes hacer es una operación aritmética que te dará como resultado el punto medio entre dos puntos. Así es como se hace:
- [(5 + 3)/2, (4 + -4)/2] =
- [(8/2), (0/2)] =
- (4, 0)
- El punto medio entre los puntos (5,4) y (3, -4) es (4,0).

Método 2

Método 2 de 2:
Hallar el punto medio de líneas horizontales o verticales

1
Encuentra una línea vertical u horizontal. Antes de que puedas utilizar este método, deberás saber cómo encontrar una línea vertical u horizontal. Así es como la encuentras:
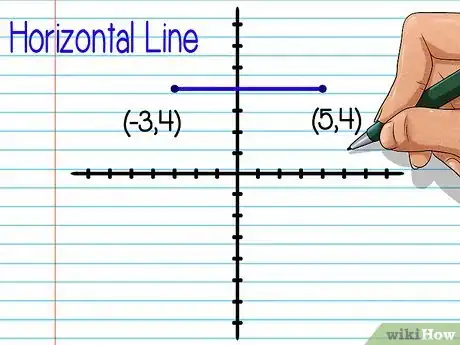
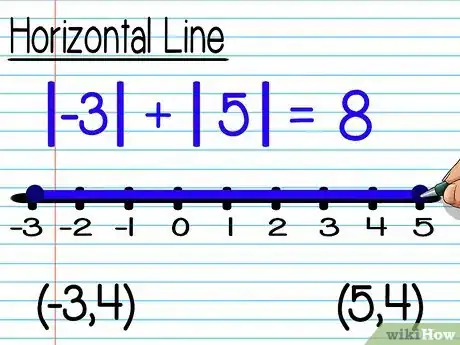
- Una línea es horizontal si las dos coordenadas y de los puntos extremos son iguales. Por ejemplo, el segmento de línea con los extremos (-3, 4) y (5, 4) es horizontal.
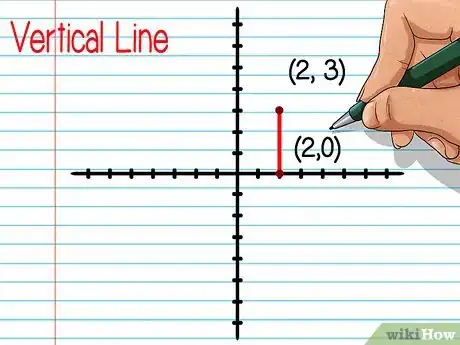
- Una línea es vertical si las dos coordenadas x de los puntos extremos son iguales. Por ejemplo, el segmento de línea de los puntos extremos (2, 0) y (2, 3) es vertical.
2
Encuentra la longitud del segmento. Puedes encontrar fácilmente la longitud del segmento contando los espacios horizontales si la línea es horizontal, o los verticales si la línea es vertical. Así es como se hace:
- El segmento de la línea horizontal con los puntos extremos (-3, 4) y (5, 4) mide 8 unidades. Puedes llegar a este número contando los espacios que hay entre un punto y el otro o restando las coordenadas x y sacando su valor absoluto: |(-3) - 5 |= |-8|= 8
- El segmento de la línea vertical con los puntos extremos (2, 0) y (2, 3) mide 3 unidades. Puedes llegar a este número contando los espacios que hay entre un punto y el otro o restando las coordenadas y y sacando su valor absoluto: |0 - 3| = |-3| = 3
3
Divide la longitud del segmento entre dos. Ahora que conoces la longitud del segmento, divídelo entre dos.
- 8/2 = 4
- 3/2 = 1,5
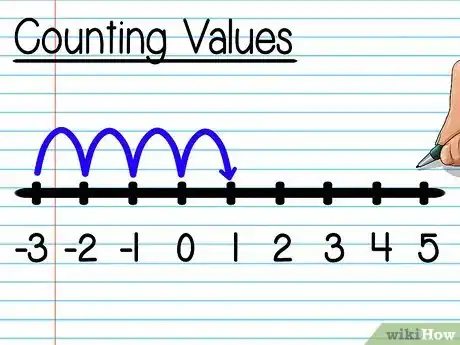
4
Cuenta ese valor desde cualquiera de los puntos extremos. Este es el último paso para encontrar el punto medio de un segmento de recta. Así es como se hace:
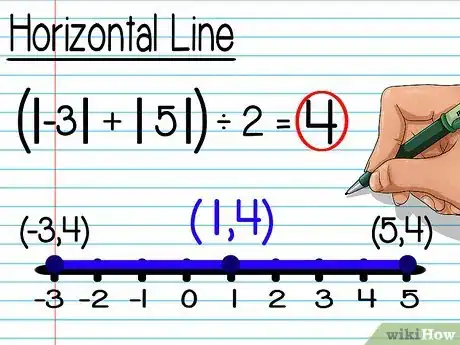
- Para encontrar el punto medio entre los puntos (-3, 4) y (5, 4), tan solo muévete 4 unidades ya sea desde la izquierda o desde la derecha para llegar a la mitad del segmento. Si nos movemos 4 unidades desde (-3, 4) llegamos al punto medio (1, 4). No tendrás que cambiar las coordenadas y ya que sabes que el punto medio se encontrará sobre la misma coordenada que los puntos extremos. El punto medio entre (-3, 4) y (5, 4) es (1, 4).
- Para encontrar el punto medio entre los puntos (2, 0) y (2, 3), tan solo muévete 1.5 unidades ya sea desde arriba o desde abajo para llegar a la mitad del segmento. Si nos movemos 1,5 unidades hacia arriba desde (2, 0) llegaremos al punto (2, 1,5). No tendrás que cambiar el valor de la coordenada x ya que sabemos que el punto medio estará en la misma coordenada x que los puntos extremos. El punto medio entre (2, 0) y (2, 3) es (2, 1,5).