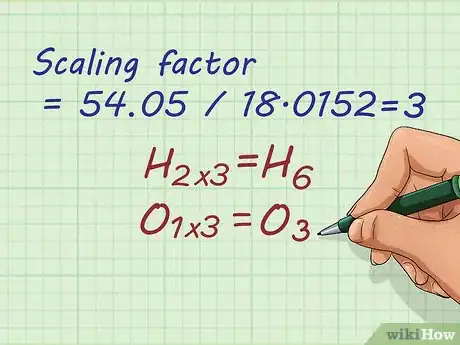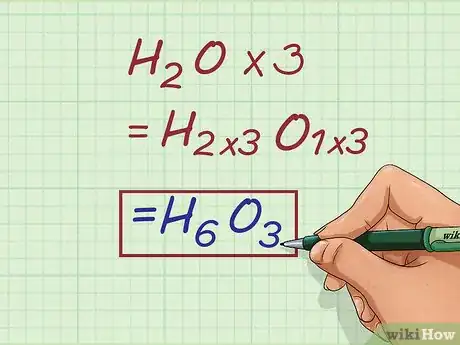Cómo encontrar un factor de escala

El factor de escala o factor de escala lineal es la proporción entre la longitud del mismo lado en dos figuras similares. El término "figuras similares" se refiere a figuras que tengan la misma forma pero diferentes tamaños. El factor de escala sirve para resolver problemas básicos de geometría y puedes usarlo para encontrar la longitud del lado de una figura. También puedes calcular el factor de escala a partir de las longitudes de los lados de dos figuras similares. Para ello, debes realizar multiplicaciones o simplificar fracciones.

Método 1

Método 1 de 4:
Encontrar el factor de escala de dos figuras similares

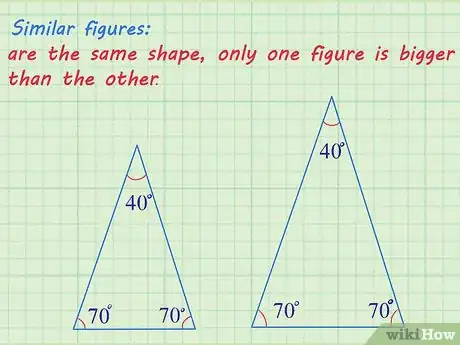
1
Asegúrate de que las figuras sean similares. Esto se refiere a dos figuras cuyos ángulos sean congruentes y cuyos lados sean proporcionales unos a otros. Dos figuras similares tienen la misma forma pero una es más grande que la otra.^{[1]
X
Fuente de investigación}
- El problema en cuestión debe especificar que las figuras son similares o indicar que los ángulos de ambas son iguales y que los lados de una de ellas son proporcionales a los de la otra, a escala, o que corresponden unos a otros.
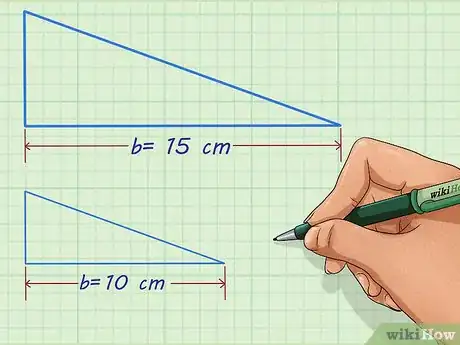
2
Identifica los lados de las figuras que corresponden unos a otros. Quizás tengas que colocar ambas figuras lado a lado para poder identificar cuáles son los lados correspondientes en una y en otra. El problema debe indicar las longitudes de estos lados o deberían estar a escala para que puedas medirlos.^{[2]
X
Fuente de investigación} No podrás encontrar el factor de escala si no tienes por lo menos la longitud de uno de los lados de cada figura.
- Por ejemplo, si tienes dos triángulos similares, la base de uno de ellos medirá 15 cm y la del otro 10 cm.
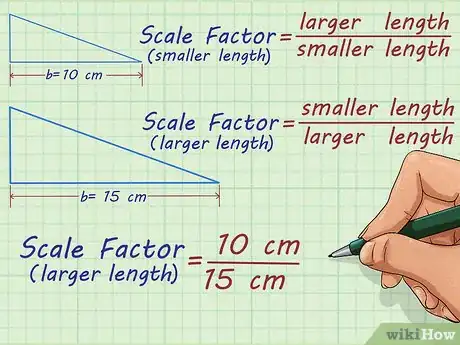
3
Establece la proporción entre los lados de ambas figuras. Cada par de figuras similares tiene dos factores de escala: el que se usa para agrandar las figuras y el que se usa para achicarlas. Si vas a agrandar una figura, debes usar la proporción ${\text{Factor de escala}}={\frac {longitudmayor}{longitudmenor}}$ ${\text{Factor de escala}}={\frac {longitudmayor}{longitudmenor}}$ . Si vas a achicar una figura, debes usar la proporción ${\text{Factor de escala}}={\frac {longitudmenor}{longitudmayor}}$ ${\text{Factor de escala}}={\frac {longitudmenor}{longitudmayor}}$ .^{[3]
X
Fuente de investigación}
- Por ejemplo, digamos que vas a reducir la escala de un triángulo cuya base mide 15 cm hasta obtener un triángulo cuya base mida 10 cm. Para esto, usarás la proporción ${\text{Factor de escala}}={\frac {longitudmenor}{longitudmayor}}$ .
  Si reemplazas los valores, obtendrás la fracción ${\text{Factor de escala}}={\frac {10}{15}}$ .
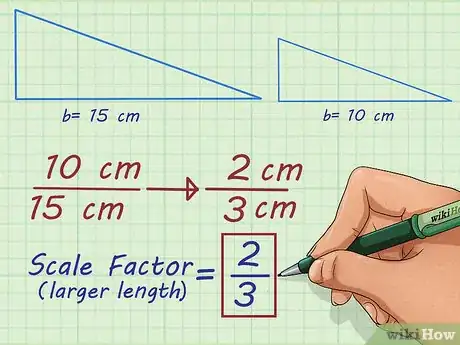
4
Simplifica la fracción. Simplifica la proporción o la fracción para obtener el factor de escala. Si vas a achicar la figura, el factor de escala será una fracción propia.^{[4]
X
Fuente de investigación} Si vas a agrandar la figura, el factor de escala será un número entero o una fracción impropia que luego puedes convertir en un número decimal.
- Por ejemplo, puedes simplificar la fracción ${\frac {10}{15}}$ hasta obtener ${\frac {2}{3}}$ . Por tanto, el factor de escala de dos triángulos cuyas bases miden 15 y 10 cm es de ${\frac {2}{3}}$ .

Método 2

Método 2 de 4:
Usar el factor de escala para trazar una figura similar

1
Encuentra la longitud de los lados de la figura. El problema debe darte la longitud de los lados de una de las figuras o debes poder medirlos. Si no es así, no podrás trazar una figura similar a la que te haya dado el problema.
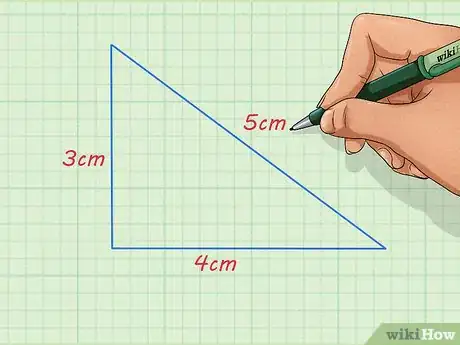
- Por ejemplo, el problema te puede haber dado un triángulo cuyos lados midan 4, 3 y 5 cm.
2
Determina si vas a reducir o incrementar la escala de la figura. Si vas a agrandar la figura original, el factor de escala será un número entero, una fracción impropia o un número decimal. Si vas a achicar la figura original, el factor de escala será una fracción propia.
- Por ejemplo, si el factor de escala es de 2, la figura similar que trazarás será más grande que la figura original.
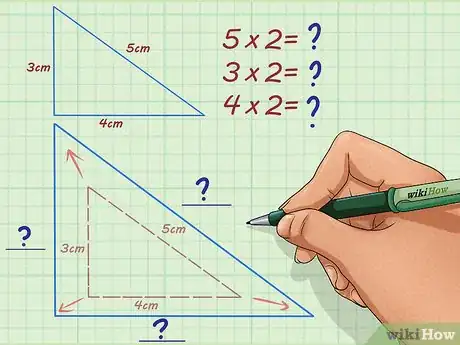
3
Multiplica la longitud de uno de los lados de la figura original por el factor de escala. El problema debe darte el factor de escala, el cual puedes multiplicar por la longitud de cada uno de los lados de la figura original para obtener la longitud de los lados correspondientes de la figura similar.^{[5]
X
Fuente de investigación}
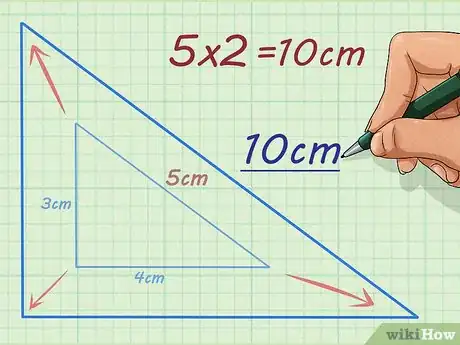
- Por ejemplo, si la hipotenusa de un triángulo rectángulo mide 5 cm y el factor de escala es de 2, debes multiplicar $5\times 2=10$ para encontrar la longitud de la hipotenusa de un triángulo similar al original. Por tanto, la hipotenusa de este triángulo similar mide 10 cm.
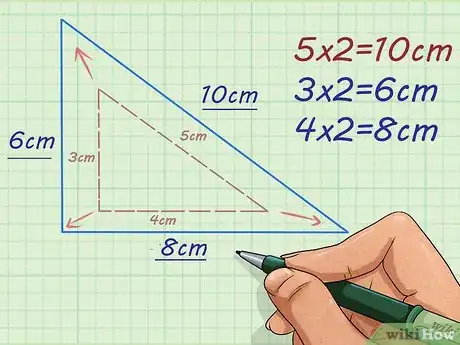
4
Encuentra la longitud de los demás lados de la figura similar. Continúa multiplicando la longitud de cada lado de la figura original por el factor de escala para obtener la longitud de los lados correspondientes de la figura similar.
- Por ejemplo, si la base de un triángulo rectángulo mide 3 cm y el factor de escala es de 2, debes multiplicar $3\times 2=6$ para obtener la longitud de la base de un triángulo similar. Si la altura de este triángulo mide 4 cm, multiplica también $4\times 2=8$ para obtener la altura del triángulo similar.

Método 3

Método 3 de 4:
Resolver problemas de ejemplo

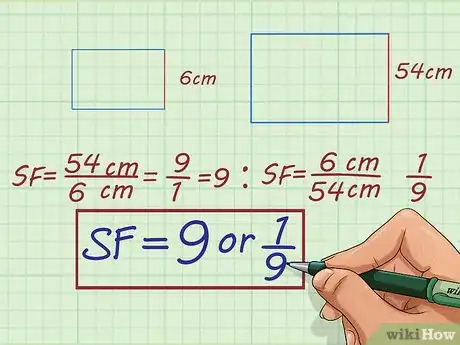
1
Encuentra el factor de escala de la siguientes figuras similares: dos rectángulos cuyas alturas miden 6 y 54 cm, respectivamente.
- Establece la proporción entre las alturas de ambos rectángulos. Para agrandar el rectángulo original, la proporción correcta es de ${\text{Factor de escala}}={\frac {54}{6}}$ y, para agrandarlo, la proporción correcta es de ${\text{Factor de escala}}={\frac {6}{54}}$ .
- Simplifica la fracción. Puedes simplificar la fracción ${\frac {54}{6}}$ hasta obtener ${\frac {9}{1}}=9$ . Asimismo, puedes simplificar la fracción ${\frac {6}{54}}$ hasta obtener ${\frac {1}{9}}$ . Por tanto, el factor de escala de ambos rectángulos es de $9$ o ${\frac {1}{9}}$ .
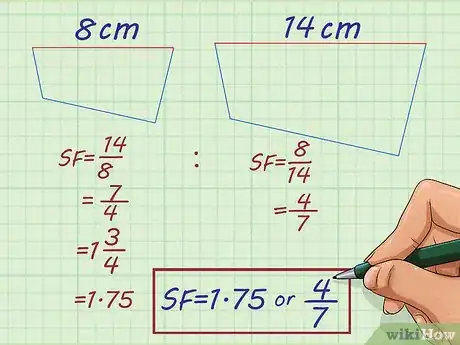
2
Intenta resolver el siguiente problema: el lado más largo de un polígono irregular mide 14 cm y el mismo lado de un polígono irregular similar mide 20 cm (8 pulgadas). ¿Cuál es el factor de escala?
- Dos figuras irregulares pueden ser similares si sus lados son proporcionales. Por tanto, es posible calcular el factor de escala con las dimensiones dadas.^{[6]
  X
  Fuente de investigación}
- Como tienes la longitud de los lados más largos de ambos polígonos, puedes establecer una proporción entre ambos. Si quieres agrandar el polígono, la proporción correcta es de ${\text{Factor de escala}}={\frac {14}{8}}$ , mientras que, si quieres achicarlo, la proporción correcta es de ${\text{Factor de escala}}={\frac {8}{14}}$ .
- Simplifica la fracción. Puedes simplificar la fracción ${\frac {14}{8}}$ hasta obtener ${\frac {7}{4}}=1{\frac {3}{4}}=1,75$ y también puedes simplificar la fracción ${\frac {8}{14}}$ hasta obtener ${\frac {4}{7}}$ . Por tanto, el factor de escala de ambos polígonos irregulares es de $1,75$ o ${\frac {4}{7}}$ .
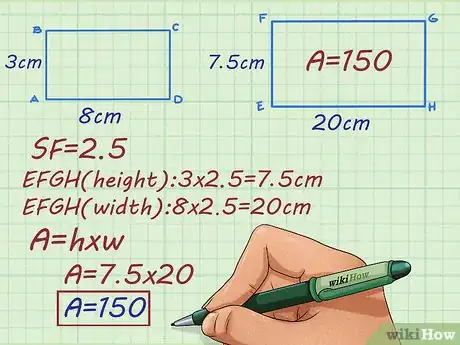
3
Utiliza el factor de escala para resolver el siguiente problema: el rectángulo ABCD mide 8 x 3 cm y el rectángulo EFGH es similar a este pero más grande. Si el factor de escala es de 2,5, ¿cuál es el área del rectángulo EFGH?
- Multiplica el ancho del rectángulo ABCD por el factor de escala para obtener el ancho del rectángulo EFGH: $3\times 2,5=7,5$ .
- Multiplica la longitud del rectángulo ABCD por el factor de escala para obtener la longitud del rectángulo EFGH: $8\times 2,5=20$ .
- Multiplica el ancho y la longitud del rectángulo EFGH para encontrar el área: $7,5\times 20=150$ . Entonces, el área del rectángulo EFGH mide 150 centímetros cuadrados.

Método 4

Método 4 de 4:
Encontrar el factor de escala en química

1
Divide la masa molar de un compuesto entre la masa molar de la fórmula empírica. Si tienes la fórmula empírica de un compuesto y tienes que encontrar su fórmula molecular, puedes obtener el factor de escala dividiendo la masa molar del compuesto entre la masa molar de la fórmula empírica.
- Por ejemplo, imagina que tienes que encontrar la masa molar de un compuesto de H₂O cuya masa molar es de 54,05 g/mol.
  - La masa molar de H₂O es 18,0152 g/mol.
  - Para encontrar el factor de escala, divide la masa molar del compuesto entre la masa molar de la fórmula empírica.
  - Factor de escala = 54,05 / 18,0152 = 3.
2
Multiplica la fórmula empírica por el factor de escala. Multiplica los subíndices de cada elemento de la fórmula empírica por el factor de escala que acabas de obtener para encontrar la fórmula molecular del compuesto químico dado en el problema.
- Por ejemplo, para obtener la fórmula molecular del compuesto, debes multiplicar los subíndices de la fórmula H₂O por el factor de escala de 3.
  - H₂O * 3 = H₆O₃.
3
Anota la respuesta. Después de realizar esta operación, habrás encontrado la fórmula empírica y la fórmula molecular del compuesto químico dado en el problema.
- Por ejemplo, si el compuesto tiene un factor de escala de 3, su fórmula molecular será H₆O₃.