Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
En este artículo, hay 12 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 3912 veces.
El tema de los decimales puede ser complicado. Por ello, es importante dividirlo en pasos para enseñarlo. Primero, se debe explicar el valor posicional de los números enteros, como las decenas y las centenas. Puedes describir los decimales como números "intermedios" que tienen sus propios valores posicionales, como las décimas y las centésimas. Menciona que estos guardan relación con las fracciones y muéstrales a tus estudiantes cómo realizar la conversión de uno a otro. Una vez que hayas enseñado los conceptos básicos, presenta algunas operaciones matemáticas con los decimales, como sumas y restas.
Pasos
Método 1
Método 1 de 3:Explicar los conceptos básicos
-
1Para empezar, revisa el tema del valor posicional de los números enteros. Anota algunos números enteros y explica que cada uno tiene un valor posicional. Muéstrales a tus estudiantes cual corresponde a las unidades, decenas y centenas.[1]
- Por ejemplo, puedes escribir el número 382. Dile a tus estudiantes que el número más pegado a la derecha, el 2, está en el lugar de las unidades; el siguiente de su izquierda, el 8, se encuentra en el lugar de las decenas; y el más pegado a la izquierda, el 3, ocupa el lugar de las centenas.
-
2Explica que los decimales son como números "intermedios". Menciona que no todos los números son enteros. Por ejemplo, puedes empezar diciendo que 5 y 6 son números enteros, pero que existen muchos números entre ellos. Muéstrales a tus estudiantes cómo colocar la coma decimal a la derecha de las unidades y menciona que todos los números que vienen después se encuentran entre dos números enteros.[2]
- Escribe "5" y explica lo siguiente: "Si ven otro 5 luego de la coma (escribe '5,5') quiere decir que este número se encuentra entre 5 y 6."
-
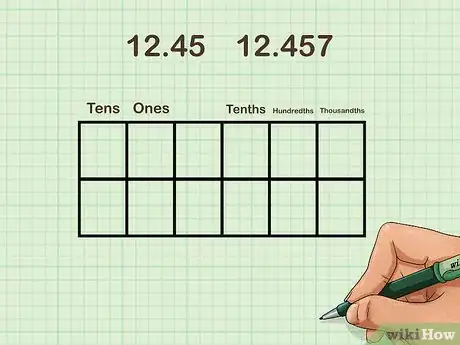
3Presenta los valores posicionales de los decimales. Explica que, al igual que con los números enteros, hay valores posicionales a la derecha de la coma decimal. Muéstrales a tus alumnos que las unidades siempre se encuentran a la izquierda de la coma decimal. Asimismo, enséñales que las décimas siempre están inmediatamente a la derecha de la coma decimal, seguidas de las centésimas y las milésimas.[3]
- Enfatiza el final de las palabras décimas y centésimas para diferenciarlas de sus contrapartes en los valores enteros, que son las decenas y las centenas, respectivamente.[4]
-
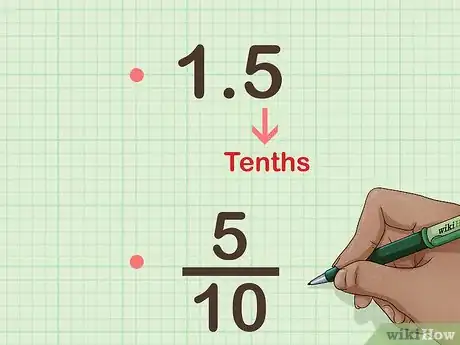
4Describe la relación entre las fracciones y los decimales. Explica que los decimales y las fracciones son dos formas de representar estos números "intermedios". Menciona que se puede convertir una fracción en un decimal y que ambos representarán el mismo número.[5]
- Es buena idea emplear cuadrículas o figuras. Por ejemplo, puedes dibujar un rectángulo y trazar líneas para dividirlo 10 partes iguales. Los estudiantes pueden colorear una de estas partes. Luego, explica que así se representa 1/10 del rectángulo. Asimismo, enséñales que también puedes escribir este mismo número como 0,1.
-
5Explica cómo convertir fracciones a decimales con divisiones. Anota algunas fracciones sencillas, como ¼, ½ y ¾. Explica que la fracción significa que el numerador se divide entre el denominador. Demuéstrale a tus estudiantes que al dividir el numerador, que es 1, entre el denominador, que es 4, te dará un valor decimal, que es 0,25.[6]
- Practica usar la división para convertir fracciones básicas a decimales. Luego, muestra cómo el valor posicional decimal, como las décimas y centésimas, se relacionan con el numerador y denominador de la fracción. Por ejemplo, 0,25 equivale a 25/100.
-
6Practica la lectura en voz alta de fracciones y decimales. Anota varios números decimales y léelos en voz alta. Enséñale a tus estudiantes a usar el valor posicional correcto al leer en lugar de que lean 1,5 como "uno coma cinco".[7]
- Escribe 25,45 y léelo en voz alta como "veinticinco con cuarenta y cinco centésimas". Escribe 54,035 y léelo como "cincuenta y cuatro con treinta y cinco milésimas".
- Luego de demostrarle a los estudiantes cómo leer los decimales, anota varios ejemplos y pídeles que los lean en voz alta. Haz correcciones si fuera necesario y no olvides animarlos con palabras amables: "Ese fue un buen intento, pero recuerda que ese número tiene valor de milésimas. Vuelve a intentarlo."
-
7Explica cómo saber saber si un número es mayor que otro. Describe la diferencia de los valores posicionales de los números enteros y de los decimales. Es decir, si bien las centenas son mayores que las decenas, las décimas son mayores que las centésimas. Coloca dos números decimales en columna, uno sobre otro, para demostrar cómo se halla el número más grande.[8]
- Por ejemplo, puedes escribir los siguientes números:
3,535
3,353 - Explica que para hallar el número mayor, deben empezar por el lugar de las décimas. Dado que 5 es mayor que 3, entonces se concluye que 3,535 es mayor que 3,353.
- Por ejemplo, puedes escribir los siguientes números:
-
8Coloca ceros para ayudar con la visualización de los valores posicionales. Tal vez a un principiante le cueste comparar números como 3,5 y 3,350, ya que 350 parece mayor que 5. En este caso, puedes decirle a tus estudiantes que coloquen ceros a la derecha del número decimal para llenar valores posicionales. Menciona que al hacer esto no se altera el valor.
- Tal vez sea más fácil entender que 3,500 es mayor que 3,350. Añadir ceros a los decimales también es útil para realizar operaciones como suma y resta.
Método 2
Método 2 de 3:Usar ayudas visuales
-
1Llena una cuadrícula para visualizar los valores decimales. Las cuadrículas con 10 a 100 espacios son muy útiles para mostrar qué es un número decimal y cómo compararlo con otros números. Puedes crear tu propia cuadrícula dibujando un rectángulo y dividiéndolo en 10 partes iguales o dibujando un cuadrado y dividiéndolo en 100 cuadrados. También puedes descargar e imprimir una cuadrícula lista.[9]
- Explica que el rectángulo o cuadrado completo vale 1. Colorea 6 espacios de los 10 y di lo siguiente: "He coloreado 6 de 10 espacios. Eso equivale a 0,6 o 6/10 (seis décimas) del total de los espacios".
- Colorea 25 espacios de un cuadrado con 100 espacios y di lo siguiente: "Hemos coloreado 25 de 100 cuadrados. Eso equivale a 0,25 o 25/100 (veinticinco centésimas) del total de los cuadrados".
- Calcula cuál número decimal es mayor coloreando las cuadrículas. Por ejemplo, puedes colorear 35 de 100 cuadrados en la primera y luego 25 de 100 cuadrados en la segunda. Explica que 35/100 es mayor que 25/100, por lo que 0,35 es mayor que 0,25.
-
2Dibuja rectas numéricas para comparar los valores. Las rectas numéricas son otra herramienta útil para enseñar que los decimales se encuentran entre los números enteros. Crea una línea horizontal con rayas verticales a cada extremo. Escribe 5 encima de la raya de la izquierda y 6 sobre la raya de la derecha.[10]
- Crea otra raya en el centro de la línea y escribe 5,5. Explica que este número se encuentra justo en el medio de 5 y 6. Pregúntale a los estudiantes dónde colocarían los valores 5,75 y 5,25, y continúa colocando más valores a lo largo de la recta.
-
3Utiliza dinero para explicar los números decimales. El dinero es una herramienta tangible excelente para enseñar este tema. Explica cómo las monedas representan 0,01, 0,05, 0,10 y 0,25, dependiendo del sistema monetario de tu país. Junta varias monedas en distintas combinaciones y úsalas para demostrar la suma y resta de decimales.[11]
Método 3
Método 3 de 3:Resolver operaciones con decimales
-
1Introduce el tema de cómo redondear números decimales. Explica que se puede redondear decimales observando el número a la derecha del valor que se desea redondear y que dicho valor posicional puede ser el de las décimas, las centésimas y así sucesivamente. Dile a los estudiantes que deben verificar si el número de la derecha del valor redondeado es mayor que o igual a 5.[12]
- Escribe 2,527 y redondéalo a la centésima más cercana. Primero, identifica el valor posicional de las centésimas en 2,527. Luego, muéstrales el número que está a la derecha. Dado que 7 es mayor que 5, se puede redondear el número a 2,53. Menciona que si el caso hubiera sido 2,522, se hubiera tenido que redondear a 2,52.
- Luego de resolver algunos ejemplos con los estudiantes, proporciónales varios ejercicios de práctica.
-
2Coloca los números uno encima del otro para sumar y restar. Haz un repaso de la suma y resta de números enteros. Dile a tus estudiantes que la suma y resta de decimales es básicamente lo mismo que con números enteros. Enfatiza la importancia de alinear la coma decimal para estas operaciones.[13]
- Recuérdales que pueden colocar ceros para llenar los espacios vacíos. Será más fácil restar 3,350 de 3,500 si pueden ver claramente todos los valores posicionales.
- Escribe algunos ejemplos y ayúdales a sumar o restar según corresponda. Luego, haz que resuelvan algunos ejercicios por su cuenta.
-
3Continúa con el tema de la multiplicación de decimales. Primero, revisa la multiplicación de números enteros. Explica que la principal diferencia entre multiplicar números enteros y decimales es que en el segundo caso, se deben sumar los lugares decimales para hallar la respuesta. El producto, que es el resultado de la multiplicación de dos números, debe tener tantos números decimales como la combinación de los lugares decimales de ambos números.[14]
- Por ejemplo, si multiplicas 2,5 por 5,5, cuenta el número de valores decimales, que es dos (cada número tiene un decimal). El producto, que es 13,75, debe tener 2 lugares decimales. Si multiplicas, 4,55 por 2,25, el producto, que es 10,2375, debe tener 4 lugares decimales.
- Trabaja algunos ejemplos con tus estudiantes y luego dales algunos ejercicios para que practiquen por su cuenta.
-
4Mueve la coma decimal hacia la derecha para dividir los decimales. Repasa el tema de las divisiones largas con números enteros antes de enseñarle a tus estudiantes a dividir números decimales. Explica que se debe mover la coma decimal del divisor (el número que divide) hacia la derecha y la coma decimal del dividendo (el número que se divide) la misma cantidad de lugares hacia la derecha.[15]
- Si vas a dividir 15,75 entre 1,5, coloca 1,5 afuera del símbolo de división y 15,75 adentro. Mueve la coma decimal hacia la derecha para convertir el número en 15. Dado que esto implica trasladar la coma un lugar, tendrás que mover la coma del número de adentro también un lugar hacia la derecha, lo que lo convertirá en 157,5.
- Coloca una coma decimal encima del símbolo de división directamente sobre la coma decimal del número de adentro (que ahora es 157,5 y no 15,75). Realiza la división de 157,5 entre 15 y te dará como resultado 10,5. Enfatiza la importancia de mover y alinear las comas decimales.
-
5Crea o descarga ejercicios para practicar. Resolver ejercicios como práctica es parte esencial de aprender matemáticas. Puedes crear tus propios ejercicios o descargar una separata lista de una página de internet, como por ejemplo Math.com (http://www.math.com/school/subject1/lessons/S1U1L2GL.html).
- Pídele a tus estudiantes que trabajen por lo menos de 10 a 15 ejercicios para aprender a identificar valor posicional, redondeo, conversión a fracciones, suma, resta, multiplicación y división. Ayúdales en los primeros dos o tres problemas y luego haz que los resuelvan solos.
- Ten paciencia y da mucho ánimo a los estudiantes durante los ejercicios. Los decimales son un tema complicado, así que haz las correcciones con amabilidad y recuérdales que es cuestión de práctica.
Referencias
- ↑ https://www.helpingwithmath.com/by_subject/decimals/dec_teaching_decimals.htm
- ↑ http://www.bbc.co.uk/bitesize/ks2/maths/number/decimals/read/2/
- ↑ https://www.helpingwithmath.com/by_subject/place_value/place_value.htm
- ↑ https://www.helpingwithmath.com/by_subject/decimals/dec_teaching_decimals.htm
- ↑ https://education.nsw.gov.au/teaching-and-learning/student-assessment/smart-teaching-strategies/numeracy/number-and-algebra/fractions-and-decimals/S2-fractions-and-decimals
- ↑ http://www.bbc.co.uk/bitesize/ks2/maths/number/decimals/read/6/
- ↑ https://www.helpingwithmath.com/by_subject/decimals/dec_teaching_decimals.htm
- ↑ http://www.bbc.co.uk/bitesize/ks2/maths/number/decimals/read/4/
- ↑ https://education.nsw.gov.au/teaching-and-learning/student-assessment/smart-teaching-strategies/media/documents2/numeracy/Fraction-Stage-2.pdf
- ↑ https://www.mathsisfun.com/decimals.html
- ↑ https://www.helpingwithmath.com/by_subject/decimals/dec_teaching_decimals.htm
- ↑ http://www.math.com/school/subject1/lessons/S1U1L3GL.html
- ↑ http://www.bbc.co.uk/bitesize/ks2/maths/number/decimals/read/3/
- ↑ http://www.math.com/school/subject1/lessons/S1U1L5GL.html
- ↑ http://www.math.com/school/subject1/lessons/S1U1L6GL.html



































wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 3912 veces.