Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 251 712 veces.
En álgebra, un binomio es una expresión de dos términos conectada por un signo de suma o resta, como por ejemplo . El primer término siempre incluye una variable, mientras que el segundo puede tener otra variable o no. Factorizar un binomio implica hallar los términos más simples que, al multiplicarse, den como resultado la expresión original, lo que te permite resolverla o simplificarla para continuar el proceso.
Pasos
Método 1
Método 1 de 3:Factorizar binomios
-
1Revisa los conceptos básicos de la factorización. Esta consiste en simplificar un número grande en sus partes divisibles más pequeñas. Cada una de estas partes se llama “factor”. Por ejemplo, el número 6 puede dividirse entre cuatro números diferentes: 1, 2, 3 y 6. Por tanto, los factores de 6 son 1, 2, 3 y 6.
- Los factores de 32 son 1, 2, 4, 8, 16 y 32.
- Tanto “1” como el número que vas a factorizar son factores. Por lo tanto, los factores de un número pequeño, como 3, serían simplemente 1 y 3.
- Los factores son solo los números divisibles o números “enteros”. Podrías dividir 32 entre 3,564 o 32,4952, pero no hallarás un factor, sino simplemente otro número decimal.
-
2Coloca los términos del binomio de tal manera que sean más fáciles de leer. Un binomio es simplemente la suma o diferencia de dos números, donde al menos uno debe incluir una variable. A veces, las variables tienen exponentes, como o . Cuando recién empiezas a factorizar binomios, puede ser útil reordenar las ecuaciones de manera ascendente; es decir, con el exponente más grande al final. Por ejemplo:
- →
- →
-
→
- Observa que el signo negativo sigue estando delante del 2. Si uno de los términos debe restarse, mantén el signo negativo delante de él.
-
3Halla el máximo factor común de ambos términos. Esto significa que debes hallar el número mayor entre el cual puedes dividir ambas partes del binomio. Si tienes dificultad para hacerlo, simplemente factoriza ambos números por separado y luego observa cuál es el número más grande que tienen en común. Por ejemplo:
-
Problema de práctica:
- Factores de 3: 1, 3
- Factores de 6: 1, 2, 3, 6
- El máximo factor común es 3.
-
Problema de práctica:
-
4Divide el máximo factor común de cada término. Una vez que halles el factor común, tendrás que eliminarlo de cada término. Sin embargo, ten en cuenta que simplemente separarás los términos, convirtiéndolos en pequeñas divisiones. Si lo haces correctamente, ambas ecuaciones compartirán el factor hallado:
- Problema de práctica:
- Halla el máximo factor común: 3
- Elimina el factor de ambos términos:
-
5Para terminar, multiplica la expresión final por el factor. En el problema anterior, se eliminó 3 para obtener . Sin embargo, realmente no te deshiciste del 3 por completo, sino que lo factorizaste para simplificar la expresión. No es posible borrar números sin volver a colocarlos. Por tanto, debes multiplicar el factor por la expresión para terminar el proceso correctamente. Por ejemplo:
- Problema de práctica:
- Halla el máximo factor común: 3
- Elimina el factor de ambos términos:
- Multiplica el factor por la nueva expresión:
- Respuesta final factorizada:
-
6Revisa tu trabajo multiplicando todo hasta llegar a la ecuación original. Si has hecho todo correctamente, revisar será un proceso sencillo. Simplemente tienes que multiplicar el factor por ambos términos dentro del paréntesis. Si el resultado es igual a la expresión original sin factorizar, todo está correcto. Resuelve la expresión desde el inicio hasta el final para practicar:
- Reorganiza los términos:
- Halla el máximo factor común:
- Elimina el factor de ambos términos:
- Multiplica el factor por la nueva expresión:
- Revisa tu respuesta:
Método 2
Método 2 de 3:Factorizar binomios para resolver ecuaciones
-
1Utiliza la factorización para simplificar ecuaciones y facilitar su resolución. Al resolver una ecuación con binomios, particularmente los más complejos, puede parecer que no hay forma de que todo encaje. Por ejemplo, intenta resolver . Una forma de hacerlo, sobre todo cuando hay exponentes, es factorizar primero.
- Problema de práctica:
- Recuerda que los binomios solo tienen dos términos. Si hay más de dos, será mejor que revises una guía para aprender a resolver polinomios.
-
2Suma y resta de tal manera que el valor de un lado de la ecuación sea cero. Esta estrategia tiene su fundamento en uno de los principios más básicos de las matemáticas: cualquier valor multiplicado por cero es igual a cero. Por lo tanto, si la expresión equivale a cero, uno de los términos factorizados debe ser cero. Para empezar, suma y resta según sea necesario hasta que uno de los lados sea igual a cero.
- Problema de práctica:
-
Iguala un lado a cero:
-
3Factoriza el lado que no es cero como lo harías normalmente. Para este paso puedes fingir que el otro lado no existe. Simplemente haya el máximo factor común, divide la expresión entre el factor y crea una expresión factorizada.
- Problema de práctica:
- Iguala un lado a cero:
- Factoriza:
-
4Iguala a cero los valores de dentro y fuera del paréntesis. En el problema de práctica, se multiplica 2y por 4 – y, y el producto debe ser 0. Dado que cualquier valor multiplicado por 0 es 0, 2y o 4 – y deben ser 0. Crea dos ecuaciones separadas para hallar el valor de “y” para que alguna de las expresiones sea 0.
- Problema de práctica:
- Iguala un lado a cero:
- Factoriza:
-
Iguala ambas partes de la expresión a 0:
-
5Resuelve ambas ecuaciones para hallar la respuesta o respuestas finales. Es posible que obtengas una respuesta o más. Recuerda que solo un lado de la ecuación debe ser igual a 0, así que quizá halles varios valores distintos para “y” que resuelvan la misma ecuación. Completa el problema de práctica:
-
- y = 0
-
- y = 4
-
-
6Reemplaza la variable con los resultados obtenidos para verificar su validez. Si has obtenido los valores correctos de “y”, deberás poder utilizarlos para resolver la ecuación. Es tan simple como reemplazar “y” con cada una de las variables como se muestra a continuación. Si las respuestas dieron como resultado que “y” puede valer 0 o 4, entonces:
-
- Esta respuesta es correcta.
-
- Esta respuesta también es correcta.
-
Método 3
Método 3 de 3:Resolver problemas más complejos
-
1Recuerda que las variables también son factores, incluso cuando tienen exponentes. Ten en cuenta que la factorización implica hallar qué números pueden dividir la expresión. Por ejemplo, es otra forma de escribir . Esto significa que puedes factorizar “x” si el otro término de la expresión también incluye esta variable. Considera a las variables como cualquier otro número. Por ejemplo:
- puede factorizarse, ya que ambos términos incluyen “t”. La respuesta final sería .
- Incluso puedes factorizar múltiples variables a la vez. Por ejemplo, en la expresión ambos términos incluyen . Por lo tanto, expresión factorizada sería .
-
2Combina los términos semejantes para reconocer binomios que no se han simplificado. Por ejemplo, utiliza la expresión . Quizá te parezca que tiene cuatro términos, pero si observas bien te darás cuenta de que son solo dos. Puedes sumar los términos semejantes. Dado que 6 y 14 no tienen una variable, y que 2x y 3x tienen la misma variable, puedes combinar estos términos. Luego de hacerlo, factorizar es más sencillo:
- Problema original:
- Reorganiza los términos:
- Combina los términos semejantes:
- Halla el máximo factor común:
- Factoriza:
-
3Reconoce el caso especial de la “diferencia de cuadrados perfectos”. Un cuadrado perfecto es un número cuya raíz cuadrada es un número entero, como , o incluso . Si el binomio del problema es la diferencia de dos cuadrados perfectos, como , puedes reemplazar la expresión con la siguiente fórmula:
- Fórmula de la diferencia de cuadrados perfectos:
- Problema de práctica:
-
Halla las raíces cuadradas:
- Reemplaza los cuadrados en la fórmula: [1]
-
4Aprende a descomponer la “diferencia de cubos perfectos”. Al igual que en el caso de los cuadrados perfectos, también existe una fórmula sencilla para cuando debes factorizar un binomio que expresa la diferencia de dos términos elevados al cubo. Por ejemplo, . Al igual que en el caso anterior, simplemente debes hallar la raíz cúbica de cada término y colocar los valores en la siguiente fórmula:
- Fórmula de la diferencia de cubos perfectos:
- Problema de práctica:
-
Halla las raíces cúbicas:
- Reemplaza los valores en la fórmula: [2]
-
5Ten en cuenta que la suma de cubos perfectos también tiene su propia fórmula. Este caso es distinto a la diferencia de cuadrados perfectos, ya que puedes hallar el resultado de la suma los cubos fácilmente, como en , con una fórmula simple. Es casi igual que la fórmula del paso anterior salvo que se intercambian los signos de suma y resta. La fórmula es tan sencilla como las otras dos antes mencionadas y lo único que debes hacer es reconocer los dos cubos en el problema:
- Fórmula de la suma de cubos perfectos:
- Problema de práctica:
-
Halla las raíces cúbicas:
- Reemplaza los valores en la fórmula: [3]
Consejos
- Ten en cuenta que no todos los binomios tienen factores comunes. Quizá algunos ya estén simplificados tanto como es posible.
- Si no estás seguro de que existe un factor común, divídelo en partes más pequeñas. Por ejemplo, si no reconoces que 16 es el factor común entre 32 y 16, empieza a dividir ambos entre 2. Al hacerlo, tendrás 16 y 8, que también pueden dividirse entre 8. Ahora tienes 2 y 1, los factores más pequeños. Evidentemente, existe un número mayor que 8 y 2 que es un factor común.
- Recuerda que la sexta potencia (x6) es ambas: un cuadrado perfecto ‘’y’’ un cubo perfecto. Como tal, puedes aplicar las dos fórmulas especiales indicadas más arriba, en cualquier orden, a un binomio que es la diferencia de valores elevados a la sexta potencia, como “x6 - 64”. Sin embargo, quizá te parezca más sencillo aplicar la fórmula de la diferencia de cuadrados perfectos primero, de tal manera que puedas factorizar el binomio de forma más completa.
Advertencias
- Un binomio que es la suma de sus cuadrados perfectos no puede factorizarse.






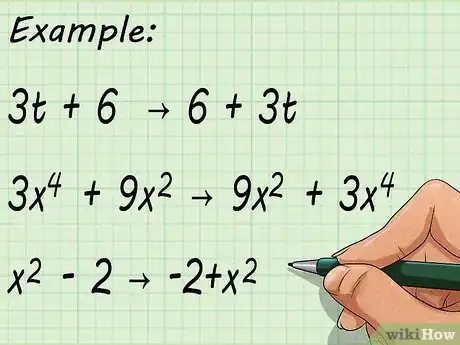























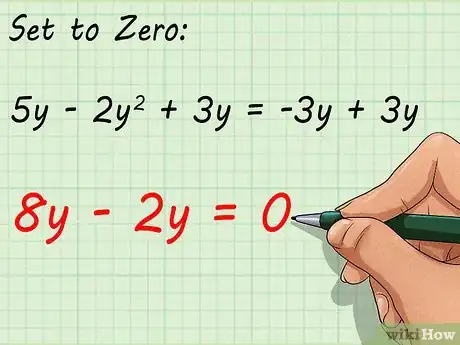








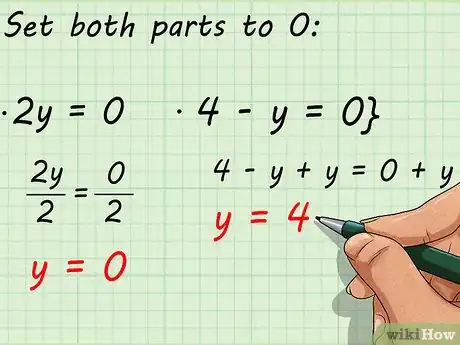


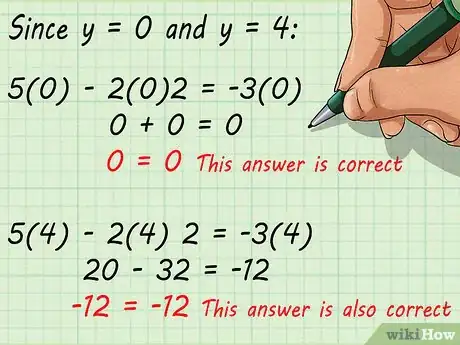



































![{\sqrt[ {3}]{8x^{3}}}=2x](./images/2122260483-77ed49f7f0ab2dfb9de3438ac123641fb683a0a0.webp)
![{\sqrt[ {3}]{27}}=3](./images/2097487987-ca5392df17ff31f62e3cae649d51dd36bde856ce.webp)
























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 251 712 veces.