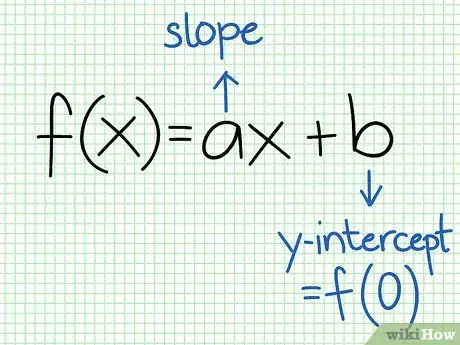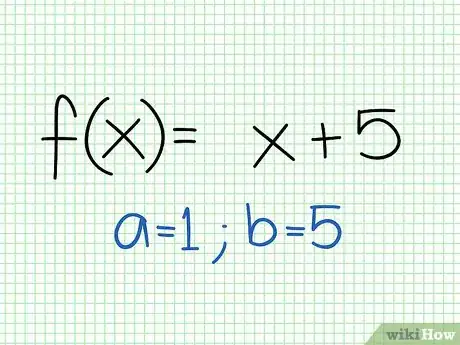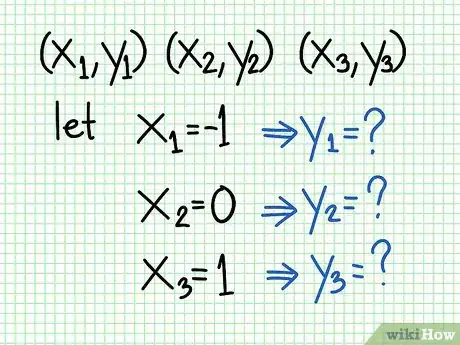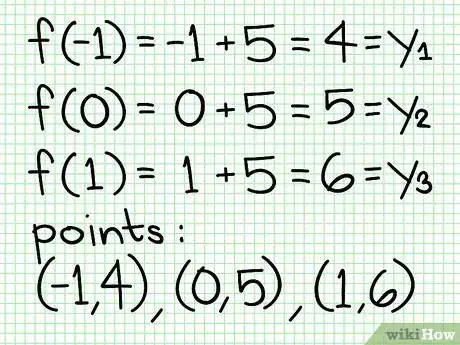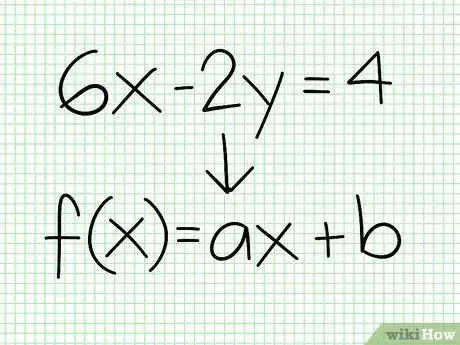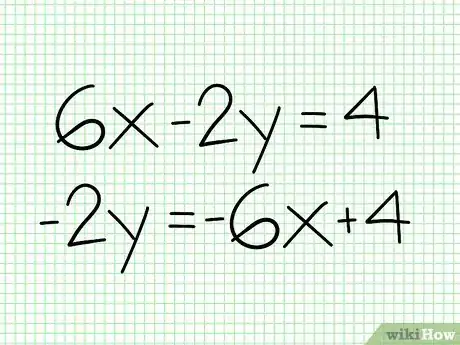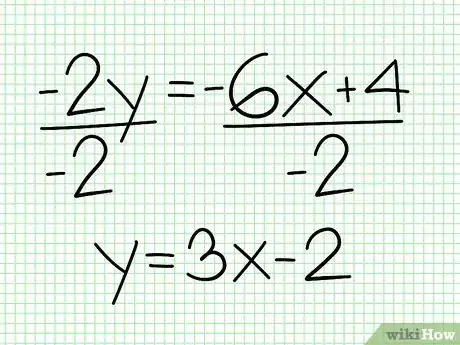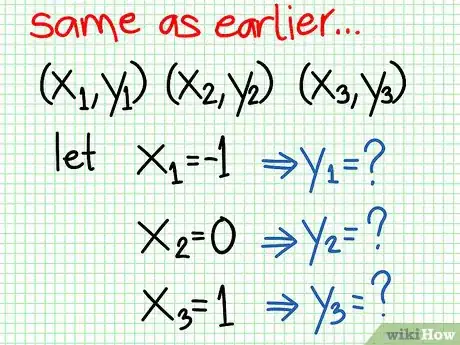X
wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, autores voluntarios han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 201 052 veces.
Algunas de las funciones más importantes son lineales: tienen razones de cambio constantes y por lo tanto se grafican con una línea recta. Podrás dibujar la línea si conoces al menos dos puntos, pero es mejor que elijas 3, de esa forma podrás asegurarte de que no hayas cometido un error. ¿Necesitas trabajar con funciones lineales? Empieza por el paso 1.
Pasos
Método 1
Método 1 de 2:Método 1: Grafica funciones lineales en su forma estándar
Método 1
-
1Reconoce la forma estándar de una función lineal. Típicamente, las funciones lineales están escritas en la forma f(x) = ax + b. La “a” representa la gradiente de la recta, lo cual da la razón de cambio de la variable dependiente. A esto se le conoce como la “pendiente”. La “b” representa el intercepto con el eje Y. Este es el valor de la variable dependiente o en otras palabras, el valor de la función cuando X = 0.
- Por ejemplo, digamos que tienes la función f(x) = x + 5. Esta es una función lineal en su forma estándar.
-
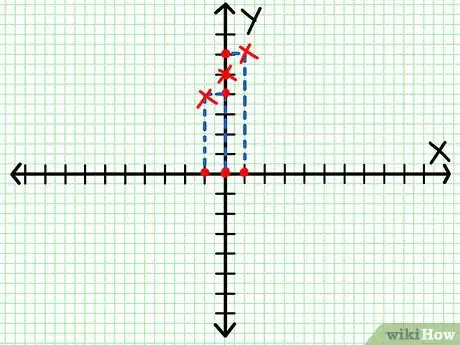
2Busca por lo menos dos puntos. Sabrás que tu gráfico tendrá una línea recta porque tienes una función lineal, por lo tanto, realmente solo necesitas dos puntos. En general, sin embargo, debes encontrar 3 puntos en lugar de 2 para revisar la precisión.
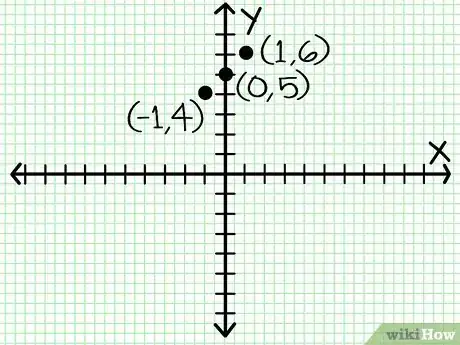
- En el ejemplo anterior, quizá puedas elegir -1, 0 y 1 para los valores de X. Resuelve como se muestra en la imagen.
-
3
-
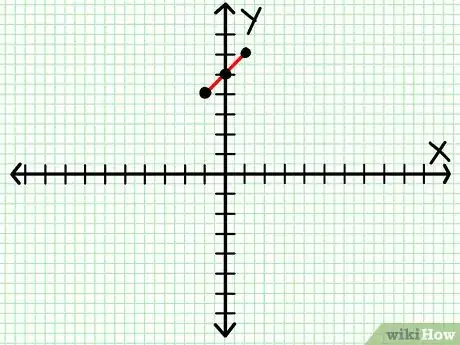
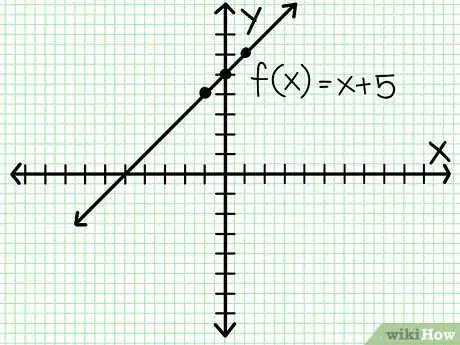
4Conecta los puntos. Para 2 puntos cualesquiera, solo hay una forma de conectarlos con una línea recta. Utiliza una regla para unirlos con una línea. Debes notar que si graficas 3 puntos y no todos caen en la misma línea, has cometido algún error. Regresa y calcula todo de nuevo.
- En el ejemplo anterior, tu gráfico debe verse así.
Método 2
Método 2 de 2:Método 2: Grafica funciones lineales en su forma no estándar
Método 2
-
1Arregla la función para hacer que la Y sea el sujeto. Si tienes una función lineal que no está en su forma estándar, deberás reescribirla antes de poder hacer el gráfico.
- Digamos que tienes la función 6x – 2y = 4. Mueve todo menos la Y a la izquierda de la siguiente manera.
- Luego divide ambos lados entre -2. Ahora tienes la forma estándar de una función lineal: y = 3x – 2.
-
2Busca por lo menos dos puntos. Sabrás que tu gráfico tendrá una línea recta porque tienes una función lineal, por lo tanto, realmente solo necesitas dos puntos. En general, sin embargo, debes encontrar 3 puntos en lugar de 2 para revisar la precisión.
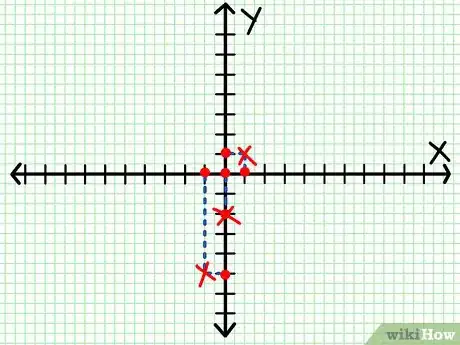
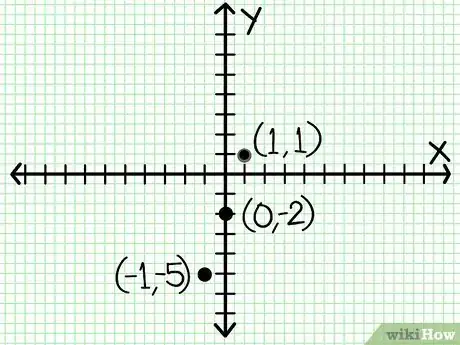
- En el ejemplo reescrito más arriba, quizá puedas elegir -1, 0 y 1 como valores de X. Resuelve de la siguiente manera.
-
3
-
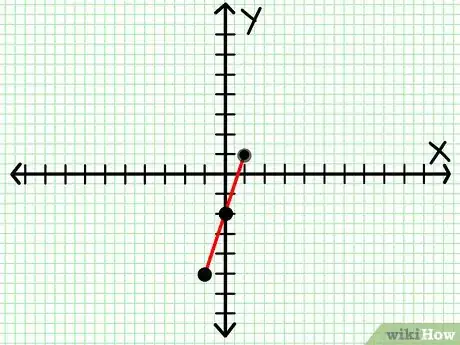
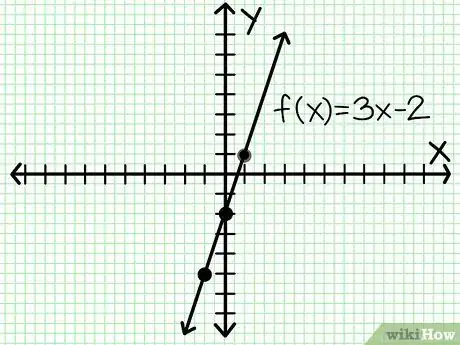
4Conecta los puntos. Para 2 puntos cualesquiera, solo hay una forma de conectarlos con una línea recta. Utiliza una regla para unirlos con una línea. Debes notar que si graficas 3 puntos y no todos caen en la misma línea, has cometido algún error. Regresa y calcula todo de nuevo.
- En el ejemplo anterior, el gráfico debe verse así.
Consejos
- Las funciones tienen una variable independiente “X” y una variable dependiente “Y”. La pendiente de una recta que pasa a través de los puntos (x1, y1) y (x2, y2) se calcula de la siguiente forma.
- Las funciones lineales tienen muchas aplicaciones prácticas, especialmente en la economía.