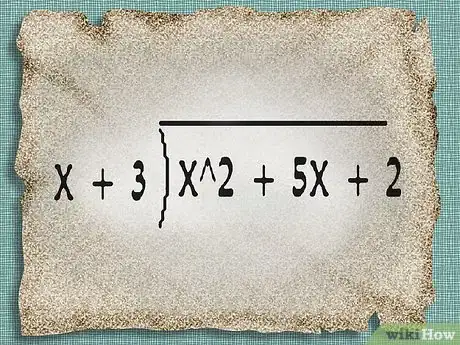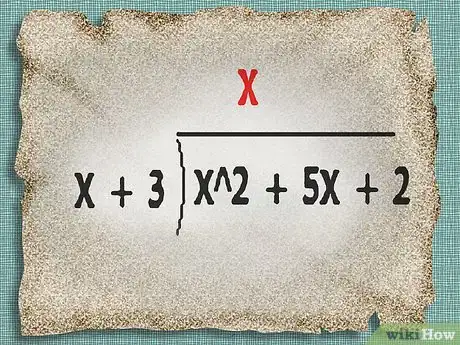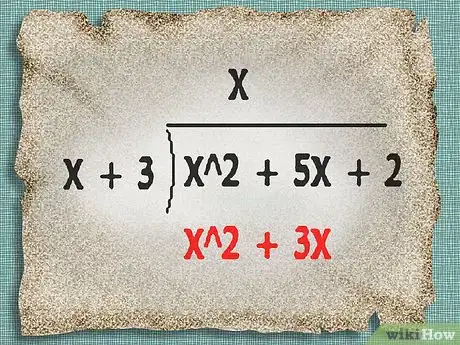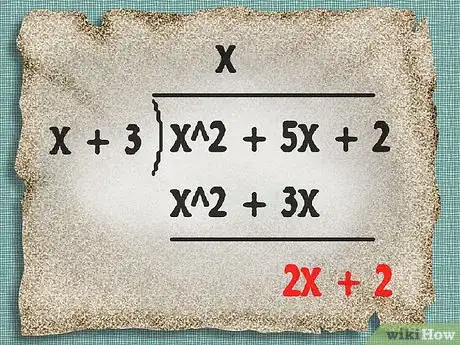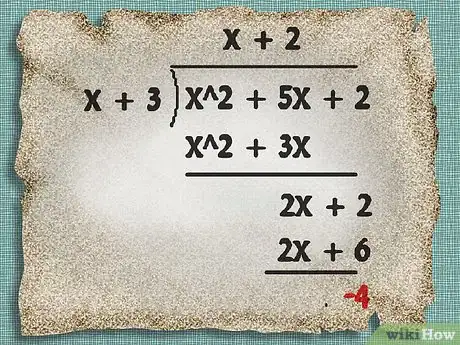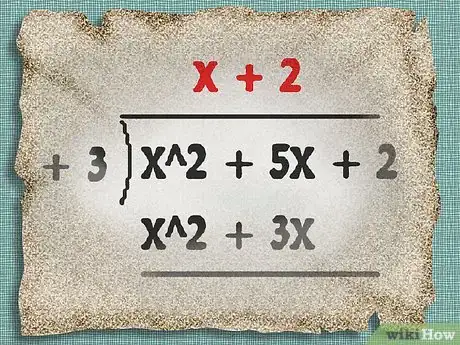Cómo hallar asíntotas oblicuas

Información del autor

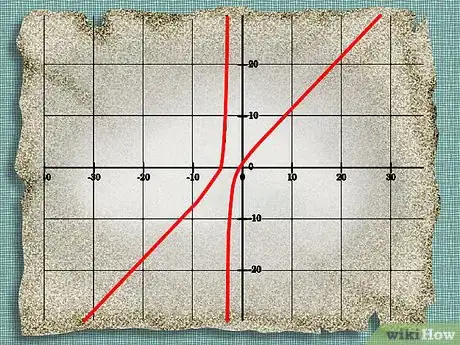
La asíntota de un polinomio es cualquier línea recta que se aproxima a su gráfico pero nunca lo toca. Puede ser vertical u horizontal, o puede ser una asíntota oblicua (es decir, una asíntota con pendiente). Un polinomio tiene una asíntota oblicua cuando el grado del numerador es mayor que el grado del denominador.

Pasos

1
Revisa el numerador y el denominador del polinomio. Asegúrate de que el grado del numerador (en otras palabras, el mayor exponente en el numerador) es mayor que el grado del denominador. Si lo es, existe una asíntota oblicua y puede hallarse.
- A manera de ejemplo, veamos el polinomio x^2 + 5x + 2 / x + 3. El grado de su numerador es mayor que el grado de su denominador, porque el numerador tiene una potencia de 2 (x^2), mientras que el denominador tiene una potencia de sólo 1. Por lo tanto, puedes hallar la asíntota oblicua. En la imagen se muestra el gráfico de este polinomio.
2
Crea un problema de división extenso. Coloca el numerador (el dividendo) dentro de la caja de división y coloca el denominador (el divisor) afuera.
- En el ejemplo anterior, establece un problema de división extenso con x^2 + 5x + 2 como el dividendo y x + 3 cómo el divisor.
3
Halla el primer factor. Busca un factor que, al multiplicarlo por el término de mayor grado en el denominador, resultará en el mismo término que el término de mayor grado en el dividendo. Escribe el factor sobre la caja de división.
- En el ejemplo anterior, deberás buscar un factor que, al ser multiplicado por x, resultará en el mismo término que el máximo grado de x^2. En este caso, este factor es x. Escribe la x sobre la caja de división.
4
Encuentra el producto del factor y de todo el divisor. Multiplica para obtener el producto y escríbelo debajo del dividendo.
- En el ejemplo anterior, el producto de x por x + 3 es x^2 + 3x. Escríbelo debajo del dividendo, tal como se muestra en la imagen.
5
Resta. Toma la menor expresión debajo de la caja de división y réstala de la expresión que se encuentra más arriba. Dibuja una línea y anota el resultado de la resta debajo de ella.
- En el ejemplo anterior, réstale x^2 + 3x a x^2 + 5x + 2. Dibuja una línea y anota el resultado, 2x + 2, debajo de ella, tal como se muestra en la imagen.
6
Continúa dividiendo. Repite estos pasos, usando el resultado del problema de resta como el nuevo dividendo.
- En el ejemplo anterior, date cuenta de que si multiplicas 2 por el mayor término del divisor (x), obtendrás el mayor grado del dividendo, que ahora es 2x + 2. Escribe 2 en la parte de arriba de la caja de división y súmalo al primer factor, de modo que obtengas x + 2. Escribe el producto del factor y del divisor debajo del dividendo y réstalo nuevamente, tal como se muestra en la imagen.
7
Detente cuando obtengas una ecuación lineal. No tienes que realizar esta extensa división hasta el final. Continúa sólo hasta que obtengas una ecuación lineal de la forma ax + b, donde a y b pueden ser cualquier número.
- En el ejemplo anterior, ahora puedes detenerte. La ecuación lineal es x + 2.
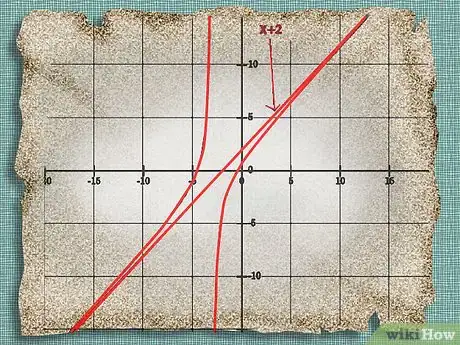
8
Dibuja la línea expresada por esta ecuación a lo largo del gráfico del polinomio. Grafica la línea para verificar que realmente es una asíntota.
- En el ejemplo anterior, deberás dibujar x + 2 para ver que la línea se encuentre a lo largo del gráfico de tu polinomio pero nunca lo toque, tal como se muestra en la imagen. Así, x + 2 es una asíntota oblicua del polinomio.
Anuncio

Consejos

La longitud del eje-x en tu plano debe ser pequeña, de modo que puedas ver con claridad que la asíntota no toca el gráfico del polinomio.
En ingeniería, las asíntotas son sumamente útiles porque crean aproximaciones de comportamientos lineales, los cuales son fáciles de analizar, para comportamientos no lineales.

Anuncio