Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 93 060 veces.
El coeficiente de correlación, que se expresa con la letra r o ρ, es la medida de la correlación lineal (relación, en términos de fuerza y dirección) entre dos variables. Varía entre -1 y +1, y el signo (+,-) se usa para indicar si la relación es positiva o negativa. Si el coeficiente de correlación es exactamente -1, entonces la relación entre las dos variables es una correlación negativa perfecta. Si el coeficiente de correlación es exactamente +1, entonces la relación es una correlación positiva perfecta. Las variables también pueden tener una correlación positiva (valores entre 0 y 1), una correlación negativa (valores entre -1 y 0) o directamente no tener correlación (0). Puedes calcular la correlación a mano usando una calculadora de correlaciones que puedes encontrar en Internet o funciones estadísticas de una buena calculadora gráfica.
Pasos
Método 1
Método 1 de 4:Hallar el coeficiente de correlación a mano
-
1Reúne los datos. Para comenzar a calcular el coeficiente de correlación, primero debes examinar tus pares de datos. Generalmente, es útil ponerlos en una tabla, ya sea vertical u horizontal. Etiqueta cada fila o columna con o .[1]
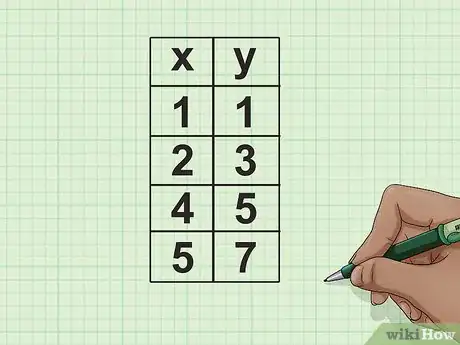
- Por ejemplo, supón que tienes cuatro pares de datos para y . Tu tabla se verá como esta:
- x || y
- 1 || 1
- 2 || 3
- 4 || 5
- 5 || 7
- Por ejemplo, supón que tienes cuatro pares de datos para y . Tu tabla se verá como esta:
-
2Calcula la media de . Para calcular la media, debes sumar todos los valores de y luego dividir entre la cantidad de valores.[2]
- En el ejemplo anterior, tienes cuatro valores para . Para calcular la media, suma todos los valores dados para y luego divide el resultado entre 4. Los cálculos deberán quedar así:
-
3Encuentra la media de . Para encontrar la media de , deberás seguir los mismos pasos, sumando los valores de , y luego dividiendo entre la cantidad de valores.[3]
- En el ejemplo anterior, también había cuatro valores para . Súmalos a todos y divide el resultado entre 4. Los cálculos deberán quedar así:
-
4Determina la desviación estándar de . Una vez que tengas el valor de las medias, ya puedes calcular la desviación estándar. Para hacerlo, usa la siguiente fórmula:[4]
- Con los datos del ejemplo, los cálculos deberán quedar así:
-
5Calcula la desviación estándar de . Usando los mismos pasos básicos, busca la desviación estándar de . La fórmula es la misma, solo que ahora tienes que reemplazar los valores por los puntos de .[5]
- Con los datos del ejemplo, los cálculos deberán quedar así:
-
6Revisa la fórmula básica para hallar el coeficiente de correlación. La fórmula para calcular un coeficiente de correlación utiliza medias, desviaciones estándar y la cantidad de pares de tu conjunto de datos (que se representa a través de la letra n). El coeficiente de correlación en sí, se representa con una letra r minúscula o con la letra griega rho minúscula, ρ. En este artículo se usará la fórmula que se conoce con el nombre de "Coeficiente de correlación de Pearson", que es la que se muestra a continuación:[6]
- Es posible que encuentres leves variaciones de la fórmula, aquí o en otros textos. Por ejemplo, algunos usan la notación griega con rho y sigma, mientras que otros usan r y s. Algunos textos pueden mostrar fórmulas con pequeñas diferencias, pero matemáticamente son todas equivalentes a esta.
-
7Encuentra el coeficiente de correlación. Ahora tienes las medias y las desviaciones estándar de tus variables así que puedes proceder a utilizar la fórmula del coeficiente de correlación. Recuerda que n representa la cantidad de valores que tienes. En los pasos anteriores, ya obtuviste los demás datos importantes que necesitas.[7]
- Usando los datos del ejemplo, ahora debes reemplazar los valores en la fórmula del coeficiente de correlación y hacer los siguientes cálculos:
-
[
]
-
8Interpreta los resultados. Para este conjunto de datos, el coeficiente de correlación es de 0,988. Este número te indica dos cosas acerca de tus datos. Observa el signo del número y su tamaño.[8]
- Debido a que el coeficiente de correlación es positivo, puedes afirmar que hay una correlación positiva entre los datos de y los datos de . Esto quiere decir que a medida que se incrementan los valores de , también se incrementan los valores de .
- Debido a que el coeficiente de correlación es un valor muy cercano a +1, los datos de y los datos de están estrechamente relacionados. Si graficas esos puntos verás que forman una buena aproximación a una línea recta.
Anuncio
Método 2
Método 2 de 4:Obtener la correlación usando una calculadora en línea
-
1Busca una calculadora de correlación en Internet. La medida de correlación es un cálculo bastante habitual para los estadísticos. Este cálculo puede volverse muy tedioso si se hace a mano con grandes conjuntos de datos. En consecuencia, se han desarrollado varias calculadoras de correlación que se encuentran disponibles en línea. Abre cualquier buscador de Internet e ingresa el término "calculadora de correlación".
-
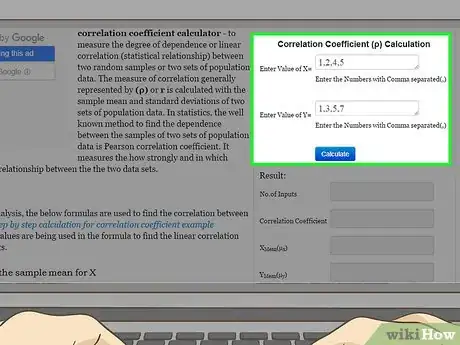
2Ingresa los datos. Revisa cuidadosamente las instrucciones del sitio web para asegurarte de ingresar los datos correctamente. Es importante que escribas los pares de datos en orden ya que podrías obtener un resultado de correlación incorrecto. Cada sitio web tiene su propio formato para la entrada de datos.
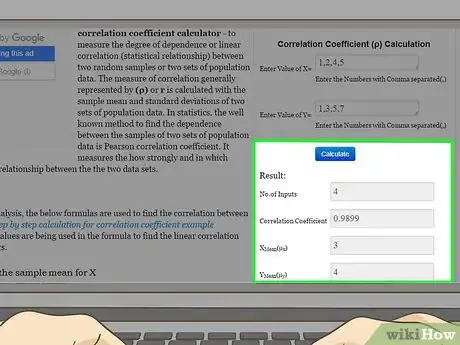
- Por ejemplo, si usas este sitio web, encontrarás un cuadro horizontal para los valores de y un segundo cuadro horizontal para los valores de . Debes ingresar los términos separados por coma. Por lo tanto, si usas los datos del ejemplo que se menciona más arriba en este artículo, los valores de debes ingresarlos así: 1,2,4,5. Los valores de serían: 1,3,5,7.
- En otros sitios, como por ejemplo este, puedes ingresar los datos vertical u horizontalmente, siempre y cuando mantengas el orden de los puntos de datos.
-
3Calcula los resultados. Estos sitios de calculadoras son muy populares porque, generalmente, después de ingresar los datos solo tienes que hacer clic en un botón que dice "Calcular" (o, si está en inglés, "Calculate") y el resultado aparece automáticamente.Anuncio
Método 3
Método 3 de 4:Usar una calculadora gráfica
-
1Ingresa los datos. Si vas a usar una calculadora gráfica de mano, selecciona el modo de función estadística y luego selecciona el comando "Edit" o "Editar".[9]
- Los comandos de teclas de las calculadoras pueden variar levemente. En este artículo, se explican las instrucciones específicas para una calculadora Texas Instruments TI-86.
- Para entrar en el modo de función estadística, debes presionar 2nd+Stat (arriba de la tecla +) y luego F2+Edit.
-
2Borra los datos viejos almacenados. La mayoría de las calculadoras guarda los datos estadísticos hasta que los borras. Para asegurarte de no confundir datos viejos con datos nuevos, es mejor que borres toda la información almacenada de operaciones anteriores.[10]
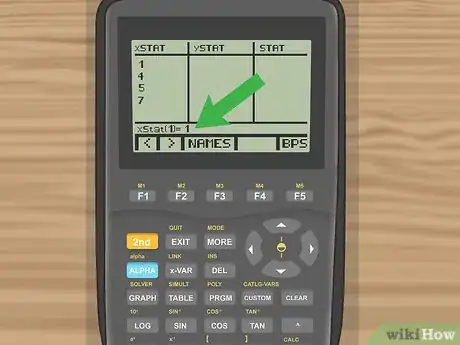
- Utiliza las teclas de las flechas para mover el cursor y seleccionar el encabezado "xStat". Luego presiona ⎚ Clear y ↵ Enter. Ahora se borrarán todos los datos de la columna "xStat".
- Ahora usa las teclas de las flechas para seleccionar el encabezado "yStat". Presiona ⎚ Clear y ↵ Enter para vaciar también los datos de esa columna.
-
3Ingresa los valores de datos. Usando las teclas de las flechas, mueve el cursor al primer espacio debajo del encabezado "xStat". Escribe el valor del primer dato y luego presiona ↵ Enter. Ahora aparecerá un espacio en la parte inferior de la pantalla que dice "xStat(1)=__ " con el valor que ingresaste en el lugar vacío. Cuando presiones ↵ Enter los datos completarán la tabla, el cursor se moverá a la línea siguiente y la línea de la parte inferior de la pantalla ahora dirá "xStat(2)=__".[11]
- Continúa ingresando todos los valores de los datos de .
- Cuando hayas terminado de cargar los datos de , usa las teclas de las flechas para desplazarte a la columna "yStat" e ingresar los valores de los datos de .
- Una vez que hayas terminado de ingresar todos los datos, presiona ↵ Enter para limpiar la pantalla y salir del menú "Stat".
-
4Calcula las estadísticas de regresión lineal. El coeficiente de correlación es una medida de qué tanto se aproximan los datos a una línea recta. Las calculadoras gráficas con funciones estadísticas pueden calcular rápidamente la línea de tendencia que representa los valores ingresados y su correspondiente coeficiente de correlación.[12]
- Ingresa en la función "Stat" y presiona el botón Calc. En el modelo TI-86, puedes hacerlo con las teclas 2nd+Stat+F1.
- Selecciona el cálculo de regresión lineal. En el modelo TI-83 está en la tecla F3 y tiene la etiqueta "LinR". La pantalla gráfica ahora mostrará "LinR_" y el cursor comenzará a parpadear.
- Ahora tienes que ingresar los nombres de las dos variables que quieres calcular. Estas variables son "xStat" y "yStat".
- En el modelo TI-86 hay que seleccionar la lista "Names" (nombres) presionando 2nd+List+F3.
- La línea inferior de la pantalla ahora mostrará las variables disponibles. Elige "xStat" (generalmente se hace presionando el botón F1 o F2), luego ingresa una coma y finalmente elige "yStat".
- Presiona ↵ Enter para calcular los datos.
-
5Interpreta los resultados. Cuando presiones ↵ Enter la calculadora calculará instantáneamente la siguiente información a partir de los datos que ingresaste:[13]
- : esta es la fórmula general de una línea recta; sin embargo, en vez de usar la típica fórmula "y=mx+b", aquí aparece representada en orden inverso.
- : este es el valor de intersección de la línea de tendencia con el eje .
- : esta es la pendiente de la línea de tendencia.
- : este es el coeficiente de correlación.
- : esta es la cantidad de pares de datos que se usaron en el cálculo.
Anuncio
Método 4
Método 4 de 4:Repasar los principios básicos de una correlación
-
1Comprende el concepto de correlación. La correlación se refiere a una relación estadística entre dos cantidades. El coeficiente de correlación es solo un número que puedes calcular para cualquier par de conjuntos de puntos de datos. Este número siempre estará entre -1 y +1 e indica qué tan estrechamente conectados tienden a estar dos conjuntos de datos.[14]
- Por ejemplo, si midieras las estaturas y edades de niños de hasta 12 años de edad aproximadamente, sería esperable encontrar una fuerte correlación positiva. A medida que los niños van creciendo, tienden a aumentar su estatura.
- Un ejemplo de correlación negativa se podría obtener comparando el tiempo que una persona dedica a practicar golf y la relación con el puntaje que obtiene. A medida que la práctica aumenta, el puntaje debe disminuir.
- Finalmente, podría esperarse una correlación muy baja (ya sea positiva o negativa) entre el tamaño de zapatos de una persona y las calificaciones que esa persona obtiene en la escuela, por ejemplo.
-
2Aprende a calcular la media. La media aritmética, o "promedio", de un conjunto de datos se calcula sumando todos los valores de datos y luego dividiendo entre la cantidad de valores que hay en ese conjunto de datos. Cuando encuentres el coeficiente de correlación de tus datos, tendrás que calcular la media de cada conjunto de datos.[15]
- La media de una variable se representa colocando una línea horizontal sobre esa variable. A menudo, a la media de los conjuntos de datos de y , se le dice "x barra" o "y barra" respectivamente. Otra notación diferente para la media, es la letra griega mu en minúscula μ. Para indicar que se trata de la media de los puntos de datos de , por ejemplo, puedes escribir μx or μ(x).
- Como ejemplo, si tienes el conjunto de puntos de datos de (1,2,5,6,9,10), entonces la media de este conjunto se calcula de la siguiente manera:
-
3Ten en cuenta la importancia de la desviación estándar. En estadística, la desviación estándar mide la variación, mostrando qué tan dispersos están los números en relación a la media. Si un conjunto de números tiene una desviación estándar relativamente baja, significa que están bastante agrupados. Si un conjunto de números tiene una desviación estándar relativamente alta, significa que están ampliamente dispersos.[16]
- Simbólicamente, la desviación estándar se expresa con la letra s minúscula o con la letra griega sigma en minúscula, σ. Por lo tanto, la desviación estándar de los datos de , se puede escribir como sx o σx.
-
4Aprende a reconocer el símbolo de sumatoria. El operador "sumatoria" es uno de los operadores más comunes en matemática y se usa para representar una suma de valores. Se expresa con la letra griega sigma en mayúscula, ∑.[17]
- A modo de ejemplo, si los puntos de datos de son (1,2,5,6,9,10) entonces ∑x significa:
- 1+2+5+6+9+10 = 33.
Anuncio - A modo de ejemplo, si los puntos de datos de son (1,2,5,6,9,10) entonces ∑x significa:
Consejos
- El coeficiente de correlación a menudo se conoce con el nombre de "coeficiente de correlación del producto-momento de Pearson", en honor a su descubridor Karl Pearson.
- En general, un coeficiente de correlación superior a 0,8 (ya sea positivo o negativo) representa una correlación fuerte, mientras que un coeficiente inferior a 0,5 (una vez más, positivo o negativo) representa una correlación débil.
Advertencias
- La correlación muestra que dos conjuntos de datos están conectados de alguna manera. Sin embargo, ten mucho cuidado de no interpretar esto como una relación de causa y efecto. Por ejemplo, el tamaño de los zapatos de una persona puede tener una correlación positiva fuerte con su estatura. Sin embargo, esto no significa que cuando aumentes tu estatura tus pies también crecerán o que si tienes pies grandes tu estatura aumentará. Es algo que simplemente ocurre en forma conjunta.
Referencias
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ https://www.youtube.com/watch?v=5YKv04PcPFY
- ↑ https://www.youtube.com/watch?v=5YKv04PcPFY
- ↑ https://www.youtube.com/watch?v=5YKv04PcPFY
- ↑ https://www.youtube.com/watch?v=5YKv04PcPFY
- ↑ https://www.youtube.com/watch?v=5YKv04PcPFY
- ↑ http://whatis.techtarget.com/definition/correlation
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://ncalculators.com/statistics/correlation-coefficient-calculator.htm
- ↑ http://www.mathsisfun.com/algebra/sigma-notation.html






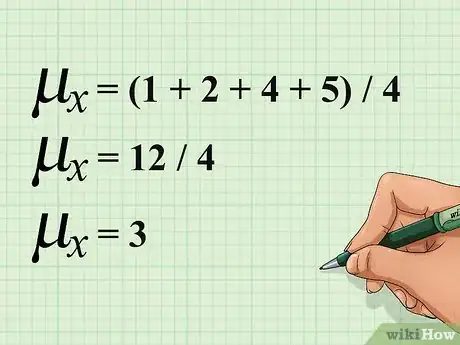



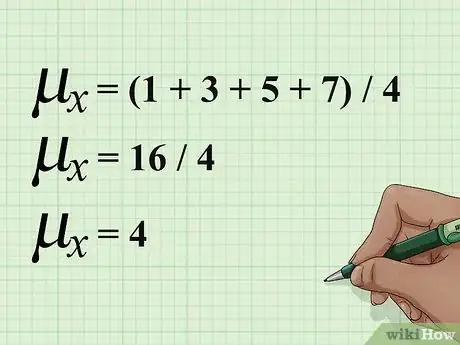



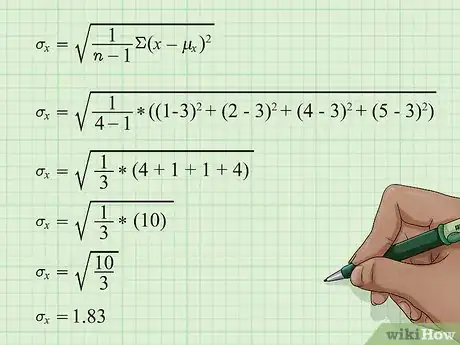






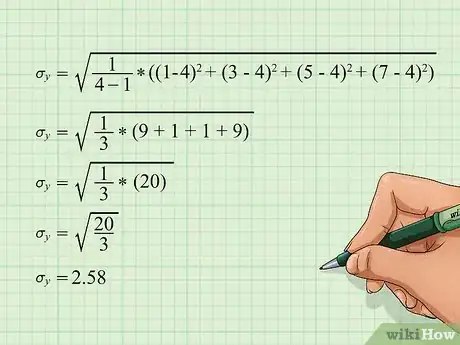





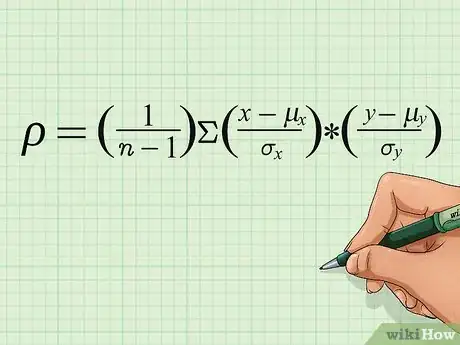

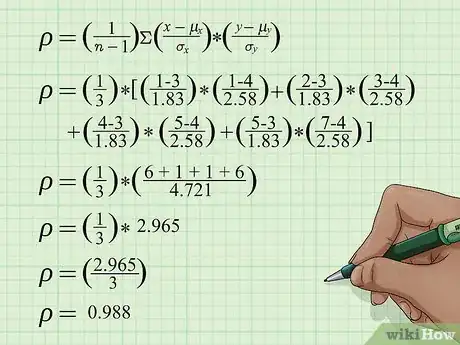



















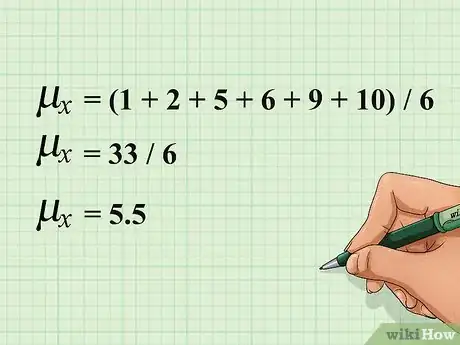



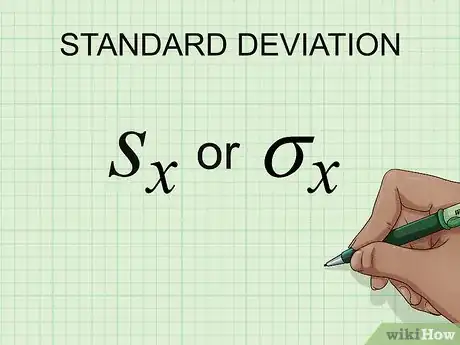




















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 93 060 veces.