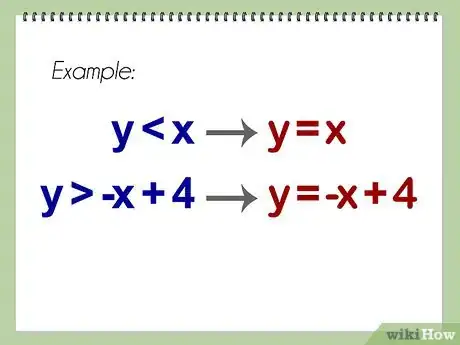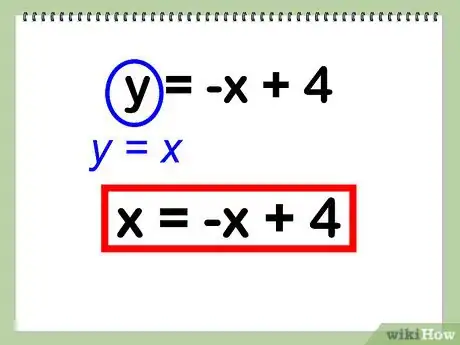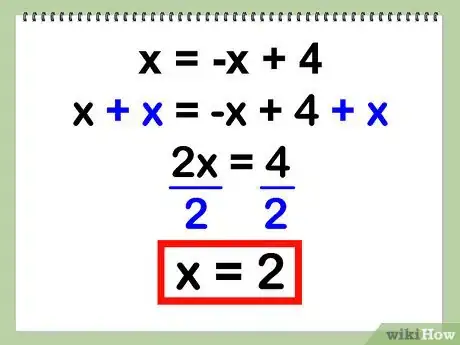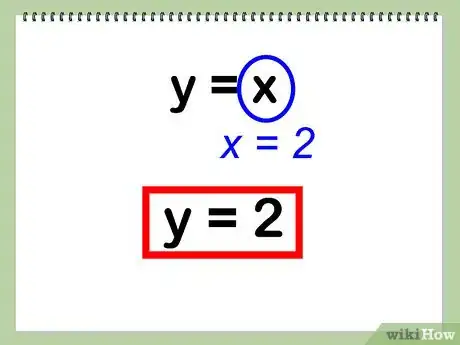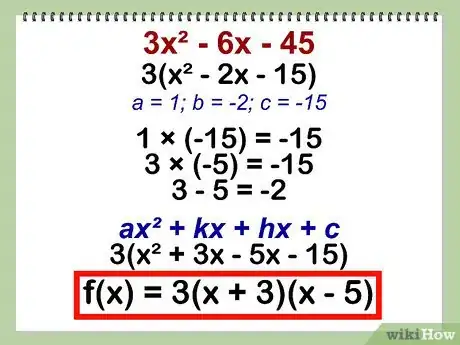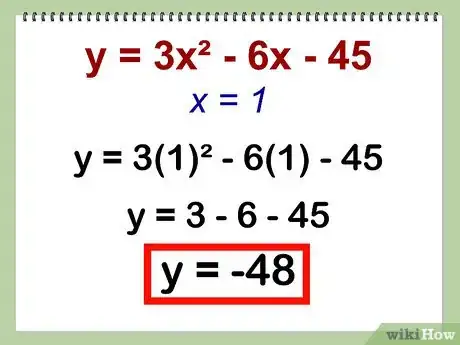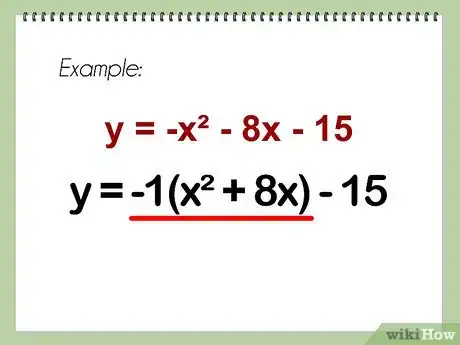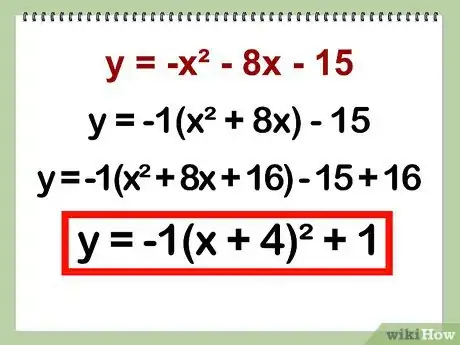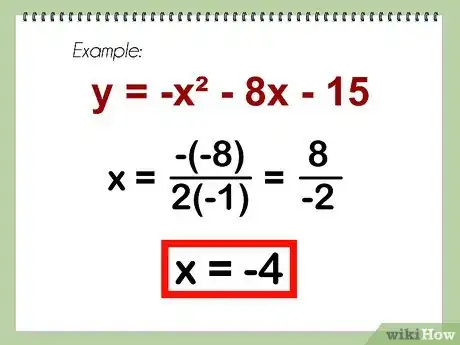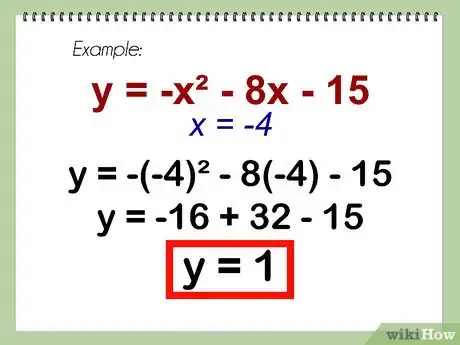Cómo hallar el vértice

Hay varias funciones matemáticas que usan vértices. Los poliedros tienen vértices, los sistemas de desigualdades pueden tener un vértice o varios vértices, y las parábolas o ecuaciones cuadráticas también pueden tener un vértice. La forma de hallar el vértice varía dependiendo de la situación, pero aquí está lo que necesitas saber sobre cómo hallar vértices en cada uno de estos escenarios.

Método 1
Método 1 de 5:
Hallar el número de vértices en un poliedro

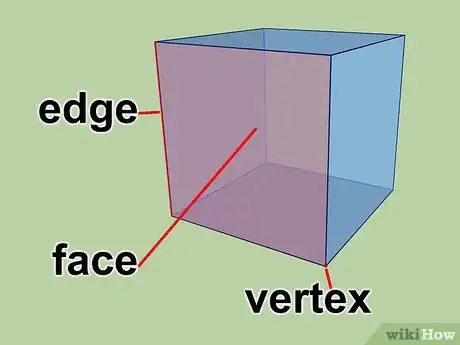
  1. Imagen titulada Find the Vertex Step 1
    1
    Aprende la formula de Euler. La fórmula de Euler, como es usada en referencia a la geometría y los gráficos, establece que para cualquier poliedro que no se interseca consigo mismo, el número de caras más el número de vértices, menos el número de aristas siempre será igual a dos.[1]
    • Escrita en forma de ecuación, la fórmula es así: C + V - A = 2
      • C es el número de caras
      • V es el número de vértices o esquinas
      • A es el número de aristas
  2. Imagen titulada Find the Vertex Step 2
    2
    Reacomoda la fórmula para hallar el número de vértices. Si conoces cuantas caras y aristas tiene el poliedro, podrás rápidamente calcular el número de vértices utilizando la fórmula de Euler. Resta C de ambos lados de la ecuación y suma A a ambos lados, despejando V a un lado.
    • V = 2 - C + A
  3. Imagen titulada Find the Vertex Step 3
    3
    Reemplaza con los números y resuelve. En este punto, todo lo que necesitas hacer es reemplazar el número de caras y aristas en la ecuación antes de sumar y restar normalmente. La respuesta que obtendrás te dará el número de vértices y la respuesta al problema.
    • Ejemplo: Para un poliedro que tiene 6 caras y 12 aristas...
      • V = 2 - C + A
      • V = 2 - 6 + 12
      • V = -4 + 12
      • V = 8

Método 2
Método 2 de 5:
Hallar vértices en un sistema de desigualdades lineales [2]

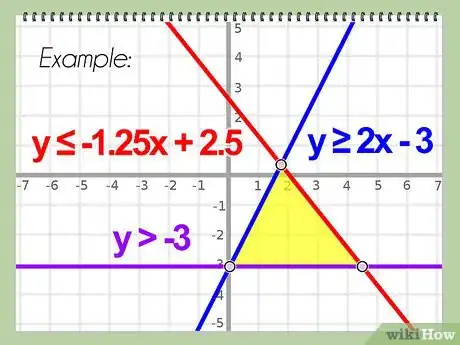
  1. Imagen titulada Find the Vertex Step 4
    1
    Grafica las soluciones para el sistema de desigualdades lineales. En algunos casos, graficar las soluciones para todas las desigualdades del sistema puede mostrarte visualmente donde están algunos, sino la totalidad, de los vértices. Sin embargo, cuando esto no resulte, deberás hallar el vértice algebraicamente.
    • Si utilizas una calculadora gráfica para graficar las desigualdades, podrás desplazarte por los vértices y encontrar sus coordenadas.
  2. Imagen titulada Find the Vertex Step 5
    2
    Cambia las desigualdades a ecuaciones. Para resolver el sistema de desigualdades, deberás cambiar momentáneamente las desigualdades a ecuaciones, permitiéndote hallar valores para x e y.
    • Ejemplo: Para el sistema de desigualdades:
      • y < x
      • y > -x + 4
    • Cambia las desigualdades a:
      • y = x
      • y = -x + 4
  3. Imagen titulada Find the Vertex Step 6
    3
    Sustituye una variable por la otra. Hay un par de formas diferentes para hallar el valor de x e y; la sustitución es casi siempre la más fácil de usar. Reemplaza el valor de y de una ecuación a la otra ecuación, "sustituyendo" efectivamente y en la otra ecuación con valores expresados con x.
    • Ejemplo: Si:
      • y = x
      • y = -x + 4
    • Entonces y = -x + 4 puede escribirse como:
      • x = -x + 4
  4. Imagen titulada Find the Vertex Step 7
    4
    Halla el valor de la primera variable. Ahora que sólo tienen una variable en la ecuación, puedes fácilmente hallar el valor de dicha variable, x, como harías en cualquier otra ecuación: sumando, restando, dividiendo y multiplicando.
    • Ejemplo: x = -x + 4
      • x + x = -x + x + 4
      • 2x = 4
      • 2x / 2 = 4 / 2
      • x = 2
  5. Imagen titulada Find the Vertex Step 8
    5
    Halla el valor de la variable restante. Reemplaza el nuevo valor de x en la otra ecuación original para hallar el valor de y.
    • Ejemplo: y = x
      • y = 2
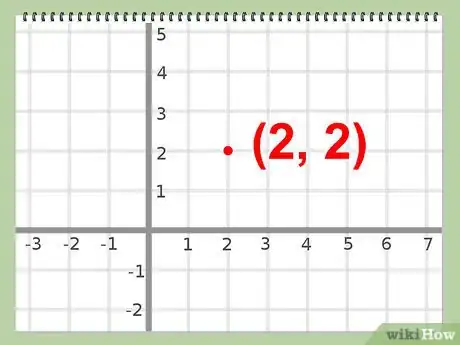
  6. Imagen titulada Find the Vertex Step 9
    6
    Determina el vértice. El vértice es simplemente la coordenada conformada por los nuevos valores de x e y.
    • Ejemplo: (2, 2)

Método 3
Método 3 de 5:
Hallar el vértice de una parábola con el eje de simetría

  1. Imagen titulada Find the Vertex Step 10
    1
    Factoriza la ecuación. Reescribe la ecuación cuadrática en su forma factorizada. Hay varias formas de factorizar una ecuación cuadrática, pero, cuando lo hagas, debes tener dos grupos de paréntesis que, al ser multiplicados, equivalen a la ecuación original.
    • Ejemplo: (usando descomposición)
      • 3x2 - 6x - 45
      • Extrae el factor común: 3 (x2 - 2x - 15)
      • Multiplica los términos a y c: 1 * -15 = -15
      • Encuentra dos números con un producto equivalente a -15 y una suma equivalente al valor b, -2: 3 * -5 = -15; 3 - 5 = -2
      • Sustituye ambos valores en la ecuación ax2 + kx + hx + c: 3(x2 + 3x - 5x - 15)
      • Factoriza el polinomio agrupando: f(x) = 3 * (x + 3) * (x - 5)
  2. Imagen titulada Find the Vertex Step 11
    2
    Encuentra el punto en el cual la ecuación cruza el eje x.[3] Cuando la función de x, f(x), equivale a 0, la parábola cruzará el eje x. Esto ocurrirá cuando cualquier grupo de factores sea equivalente a 0.
    • Ejemplo: 3 * (x + 3) * (x - 5) = 0
      • х +3 = 0
      • х - 5 = 0
      • х = -3 ; х = 5
      • Por lo tanto, las raíces son: (-3, 0) and (5, 0)
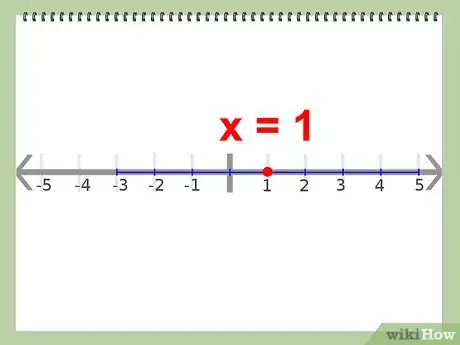
  3. Imagen titulada Find the Vertex Step 12
    3
    Calcula el punto intermedio. El eje de simetría para la ecuación estará en medio de las dos raíces de la ecuación. Necesitarás conocer el eje de simetría puesto que el vértice se encuentra en él.
    • Ejemplo: x = 1; este valor está directamente entre -3 and 5
  4. Imagen titulada Find the Vertex Step 13
    4
    Reemplaza el valor de x en la ecuación original. Reemplaza el valor de x del eje de simetría en la ecuación de la parábola. El valor de y será el valor de y en el vértice.
    • Ejemplo: y = 3x2 - 6x - 45 = 3(1)2 - 6(1) - 45 = -48
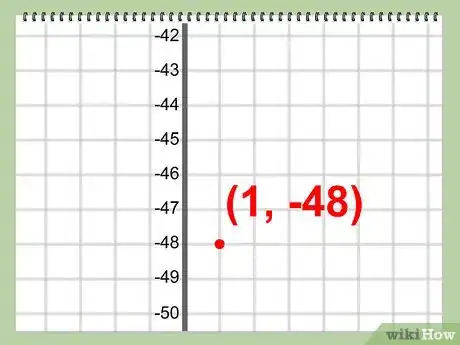
  5. Imagen titulada Find the Vertex Step 14
    5
    Escribe el punto donde se encuentra el vértice. En este punto, habrás calculado los valores de x e y, los cuales te darán las coordenadas del vértice.
    • Ejemplo: (1, -48)

Método 4
Método 4 de 5:
Hallar el vértice de una parábola completando el cuadrado

  1. Imagen titulada Find the Vertex Step 15
    1
    Reescribe la ecuación original en su forma vértice.[4] La forma "vértice" de una ecuación se escribe y = a(x - h)^2 + k, donde la ubicación del vértice es (h, k). Deberás escribir la ecuación cuadrática en esta forma y, para hacerlo, necesitarás completar el cuadrado.
    • Ejemplo: y = -x^2 - 8x - 15
  2. Imagen titulada Find the Vertex Step 16
    2
    Despeja el valor de a. Extrae el coeficiente del primer término, a, de los dos primeros términos de la ecuación. Por ahora, deja el último término c solo.
    • Ejemplo: -1 (x^2 + 8x) - 15
  3. Imagen titulada Find the Vertex Step 17
    3
    Encuentra el término para el paréntesis. El tercer término debe completar el conjunto en el paréntesis, de modo que los valores en el paréntesis formen un cuadrado perfecto. Este nuevo término se obtiene elevando al cuadrado el valor de la mitad del coeficiente del término de en medio.
    • Ejemplo: 8 / 2 = 4; 4 * 4 = 16; por lo tanto,
      • -1(x^2 + 8x + 16)
      • Ten presente que lo que hagas dentro también deberás hacerlo afuera:
      • y = -1(x^2 + 8x + 16) - 15 + 16
  4. Imagen titulada Find the Vertex Step 18
    4
    Simplifica la ecuación. Dado que los paréntesis ahora forman un cuadrado perfecto, puedes simplificar la parte parentética a su forma factorizada. Simultáneamente, puedes hacer cualquier suma o resta que se necesite para los valores fuera de los paréntesis.
    • Ejemplo: y = -1(x + 4)^2 + 1
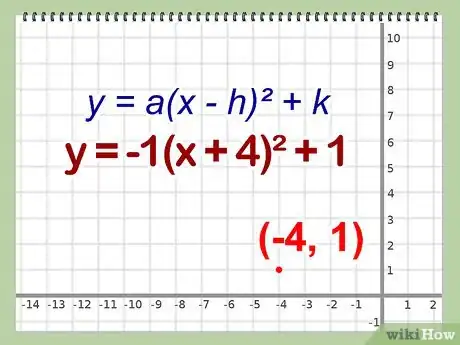
  5. Imagen titulada Find the Vertex Step 19
    5
    Encuentra las coordinadas en la ecuación en forma vértice. Recuerda que la forma vértices de una ecuación es y = a(x - h)^2 + k, donde (h, k) son las coordinadas del vértice. Ahora tienes suficiente información para reemplazar los valores de h y k, y así resolver el problema.
    • k = 1
    • h = -4
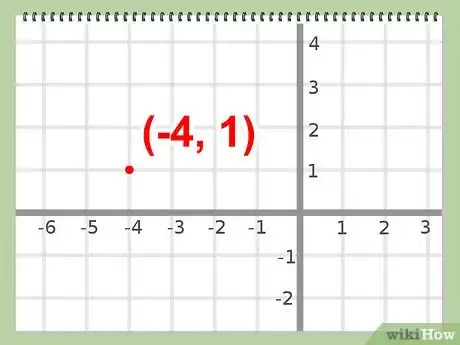
    • Por lo tanto, el vértice de esta ecuación se encuentra en: (-4, 1)

Método 5
Método 5 de 5:
Hallar el vértice de una parábola con una fórmula sencilla

  1. Imagen titulada Find the Vertex Step 20
    1
    Halla directamente la coordenada x del vértice. Cuando la ecuación de tu parábola pueda ser escrita como y = ax^2 + bx + c, la x del vértice puede hallarse usando la fórmula x = -b / 2a. Simplemente reemplaza los valores de a y b de tu ecuación en esta fórmula para hallar x.
    • Ejemplo: y = -x^2 - 8x - 15
    • x = -b / 2a = -(-8)/(2*(-1)) = 8/(-2) = -4
    • x = -4
  2. Imagen titulada Find the Vertex Step 21
    2
    Reemplaza este valor en la ecuación original. Al reemplazando el valor de x en la ecuación, podrás hallar y. Este valor de y sera la coordinada y del vértice.
    • Ejemplo: y = -x^2 - 8x - 15 = -(-4)^2 - 8(-4) - 15 = -(16) - (-32) - 15 = -16 + 32 - 15 = 1
      • y = 1
  3. Imagen titulada Find the Vertex Step 22
    3
    Escribe las coordenadas del vértice. Los valores de x e y que obtuviste son las coordenadas del vértice.
    • Ejemplo: (-4, 1)

Cosas que necesitarás

  • Calculadora
  • Lápiz
  • Papel

wikiHows relacionados

calcular el diámetro de un círculo
Cómo
calcular el diámetro de un círculo
calcular un incremento en porcentaje
Cómo
calcular un incremento en porcentaje
calcular la variación porcentual
Cómo
calcular la variación porcentual
encontrar el valor de X
Cómo
encontrar el valor de X
medir milímetros
Cómo
medir milímetros
calcular una frecuencia
Cómo
calcular una frecuencia
calcular las probabilidades de sacarte la lotería
Cómo
calcular las probabilidades de sacarte la lotería
convertir de grados a radianes
Cómo
convertir de grados a radianes
calcular la varianza
Cómo
calcular la varianza
calcular la incertidumbre
Cómo
calcular la incertidumbre
convertir radianes a grados
Cómo
convertir radianes a grados
calcular la velocidad
Cómo
calcular la velocidad
calcular el porcentaje de error
Cómo
calcular el porcentaje de error
encontrar una raíz cuadrada sin una calculadora
Cómo
encontrar una raíz cuadrada sin una calculadora

Referencias

  1. ↑ http://www.mathsisfun.com/geometry/eulers-formula.html
  2. ↑ http://faculty.nwacc.edu/colson/Interm_Alg_any/Finding%20Vertices%20for%20Systems%20of%20Linear%20Inequalities%20in%20Two%20Dimensions.pdf
  3. ↑ http://www.mathops.com/free/a1qd015.php
  4. ↑ http://mathforum.org/library/drmath/view/70241.html

Acerca de este wikiHow

wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, autores voluntarios han trabajado para editarlo y mejorarlo con el tiempo. Este artículo ha sido visto 55 863 veces.
Categorías: Matemáticas
Resumen del artículoX

Para encontrar el vértice de una parábola con eje de simetría, factoriza la ecuación cuadrática y busca el punto en el cual la ecuación cruza al eje "x". A continuación, calcula el punto intermedio, que está justo entre las dos raíces de la ecuación. Luego reemplaza el valor de “x” en cualquiera de las ecuaciones de la parábola. Los valores calculados para "x" y "y" son las coordenadas del vértice. ¡Sigue leyendo si quieres aprender a encontrar el vértice en otros escenarios matemáticos!