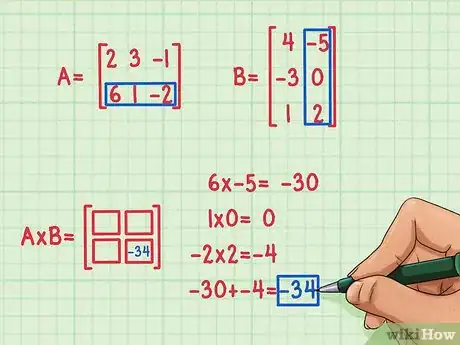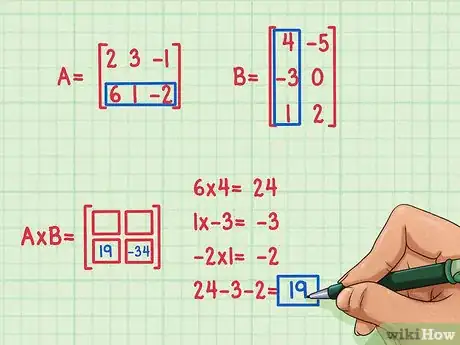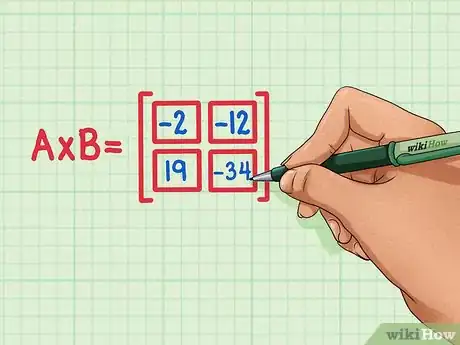Cómo multiplicar matrices

Información del autor

Una matriz es un arreglo rectangular de números o símbolos distribuidos en filas y columnas. Para multiplicar matrices, tendrás que multiplicar los elementos o números de las filas de la primera matriz por los elementos de las columnas de la segunda matriz y sumar sus productos. Puedes multiplicar matrices siguiendo sólo unos cuantos pasos muy sencillos; tendrás que sumar y multiplicar elementos, y ordenar los resultados de forma apropiada. Aquí tienes cómo hacerlo:

Pasos

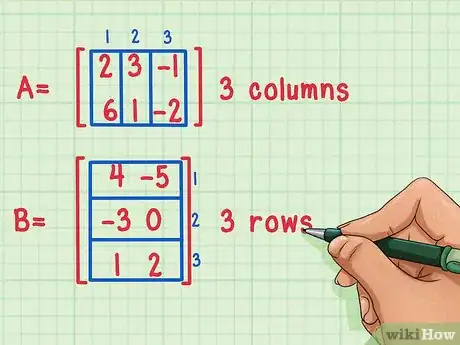
1
Asegúrate de que las matrices sean multiplicables entre sí. Sólo puedes multiplicar matrices si el número de columnas de la primera es igual al número de filas de la segunda.
- Estas matrices se pueden multiplicar porque la primera, Matriz A, tiene 3 columnas, mientras que la segunda, Matriz B, tiene 3 filas.
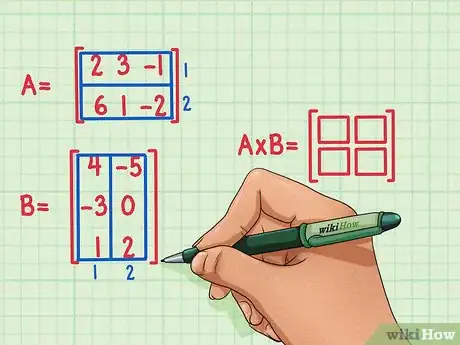
2
Marca las dimensiones del producto de matrices. Crea una nueva matriz en blanco para representar las dimensiones del producto de las dos matrices, A y B. Esta nueva matriz en blanco tendrá el mismo número de filas que la primera matriz, y el mismo número de columnas que la segunda. Puedes dibujar casillas vacías para indicar el número de filas y de columnas en esta matriz.
- La Matriz A tiene 2 filas, por lo que la el producto de matrices tendrá también 2 filas.
- La Matriz B tiene 2 columnas, por lo que el producto de matrices tendrá también 2 columnas.
- El producto de matrices tendrá 2 filas y 2 columnas.
3
Halla el primer producto escalar. Para hallar el producto escalar, tienes que multiplicar el primer elemento de la primera fila por el primer elemento de la primera columna, el segundo elemento de la primera fila por el segundo elemento de la primera columna, y el tercer elemento de la primera fila por el tercer elemento de la primera columna. Después, suma los resultados para hallar el producto escalar Imaginemos que quieres hacer esta operación con la segunda fila y la segunda columna; aquí puedes verlo:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
- El producto escalar es -34 y pertenece al elemento de la esquina inferior derecha del producto de matrices.
  - Cuando multiplicas matrices, la posición del producto escalar corresponde, verticalmente, a la de la fila de la primera matriz y, horizontalmente, a la columna de la segunda matriz de la operación. Por ejemplo, cuando hallas el producto de la última fila (abajo) de la matriz A y la última columna (a la derecha) de la matriz B, el resultado, -34, ha de colocarse en la intersección de la última fila con la última columna del producto de matrices.
4
Encuentra el segundo producto escalar. Supongamos que quieres hallar el elemento correspondiente a la esquina inferior izquierda del producto de matrices. Para hallar este elemento, simplemente tienes que multiplicar los números de la fila de abajo de la primera matriz por los elementos de la primera columna de la segunda matriz y sumarlos. Sigue el mismo método que has utilizado para multiplicar la primera fila y la primera columna. El resultado será otro de los cuatro productos escalares que hay en esta operación.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- El producto escalar es -19 y pertenece a la casilla inferior izquierda del producto de matrices.
5
Halla los dos productos escalares restantes. Para hallar el elemento de la esquina superior izquierda (es decir, el primer número de la primera fila y de la primera columna) del producto de matrices, empieza calculando el producto escalar de la primera fila de la Matriz A y la primera columna de la Matriz B. Aquí puedes ver cómo hacerlo:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
- El producto escalar es -2 y pertenece a la casilla superior izquierda del producto de matrices.
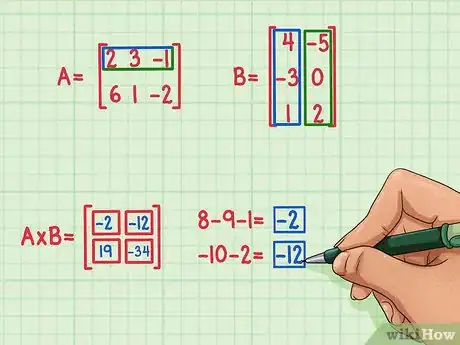
  - Para hallar el elemento correspondiente a la casilla superior derecha (es decir, el segundo número de la primera fila y primer número de la segunda columna) del producto de matrices, simplemente calcula el producto escalar de la primera fila de la Matriz A y la segunda columna de la Matriz B. Aquí puedes ver cómo hacerlo:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- El producto escalar es -12 y corresponde a la casilla superior derecha del producto de matrices.
6
Asegúrate de que los cuatro productos escalares están correctamente situados en el producto de matrices. El 19 debería estar en la esquina inferior izquierda, el -34 en la esquina inferior derecha, el -2 en la esquina superior izquierda, y el -12 en la esquina superior derecha.

Anuncio

Consejos

Usar líneas puede dar lugar a resultados erróneos si no se hace adecuadamente. Si la línea que representa una fila tiene que alargarse hasta cruzarse con una columna, no importa, ¡alárgala! Esto es sólo una técnica de visualización para aclarar qué fila y que columna tienen que utilizarse para hallar cada elemento escalar.
Escribe las sumas. Multiplicar matrices requiere realizar muchas operaciones y, aunque sean sencillas, es fácil distraerse y cometer errores a la hora de ordenar resultados o multiplicar los elementos de una fila con los de su columna correspondiente.
El producto de dos matrices debería tener el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz.

Anuncio