Cómo normalizar un vector

Información del autor

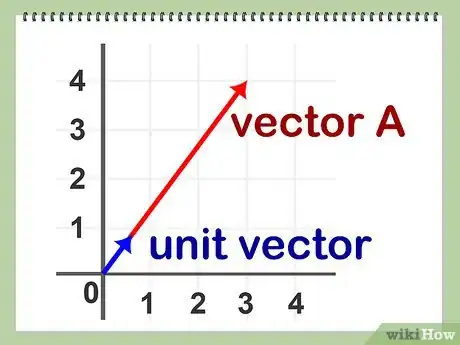
Un vector es un objeto geométrico definido por una dirección y una magnitud. Se puede representar como un segmento lineal con un punto inicial en un extremo y una flecha en el otro, de forma que su longitud indique la magnitud del vector, y la flecha indique su dirección y sentido. La normalización de vectores es un ejercicio matemático muy corriente, además de tener aplicaciones prácticas en computación gráfica.

Método 1

Método 1 de 5:
Define los términos

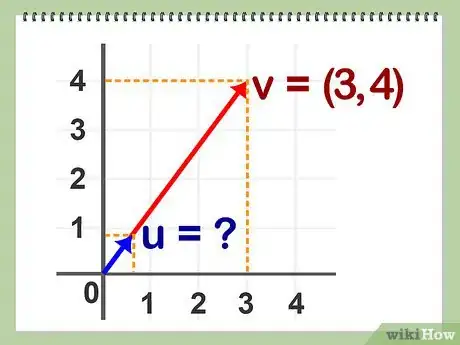
1
Define un vector unitario. El vector unitario de un vector A es aquel con el mismo punto inicial y dirección que dicho vector A, pero con una longitud de 1 unidad. Está matemáticamente demostrado que hay uno y solo un vector unitario para cada vector dado A.
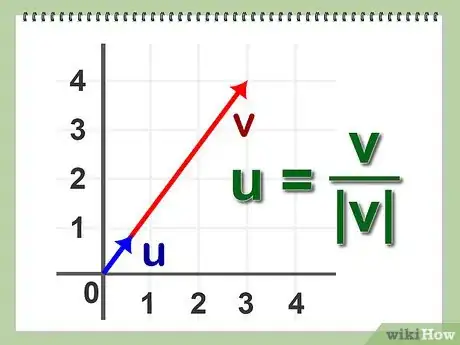
2
Define la normalización de un vector. Este es el proceso de identificar el vector unitario de un vector dado A.
3
Define un vector cuyo punto inicial se encuentre en el origen de coordenadas. Debes definir un vector que, en el espacio cartesiano, tenga su punto inicial en el origen de coordenadas, expresado como (0,0) en dos dimensiones. Esto te permitirá identificar un vector únicamente por su punto final.
4
Describe la notación vectorial. Si limitamos un vector A = (x, y), el par de coordenadas (x, y) indicará dónde se encuentra el punto final de dicho vector.

Anuncio

Método 2

Método 2 de 5:
Analiza el objetivo

1
Establece los valores conocidos. Según la definición de vector unitario, sabemos que el punto inicial y la dirección de este son iguales que los del vector dado A. Además, sabemos que la longitud del vector unitario es 1.
2
Determina el valor desconocido. La única variable que tenemos que calcular es el punto final del vector unitario.

Anuncio

Método 3

Método 3 de 5:
Deriva una solución para el vector unitario

Haya el punto final del vector unitario perteneciente al vector A = (x, y). Gracias a la relación de proporcionalidad que existe entre triángulos similares, sabemos que cualquier vector con la misma dirección que el vector A tendrá un punto final (x/c, y/c) para cierto valor de c. Además, sabemos que la longitud del vector unitario es 1. Por lo tanto, usando el teorema de Pitágoras, [x^2/c^2 + y^2/c^2]^(1/2) = 1 -> [(x^2 + y^2)/c^2]^(1/2) -> (x^2 + y^2)^(1/2)/c = 1 -> c = (x^2 + y^2)^(1/2). Entonces, el vector unitario u para el vector A = (x, y) estará definido por u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2))

Método 4

Método 4 de 5:
Normaliza un vector en un espacio bidimensional

Supongamos que el vector A es un vector con su punto inicial en el origen de coordenadas y su punto final en el punto (2, 3), de forma que A = (2,3). Calcula el vector unitario u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2)) = (2/(2^2 + 3^2)^(1/2), 3/(2^2 + 3^2)^(1/2)) = (2/(13^(1/2)), 3/(13^(1/2))). Por lo tanto, A = (2,3) quedará normalizado como u = (2/(13^(1/2)), 3/(13^(1/2))).

Método 5

Método 5 de 5:
Normaliza un vector en un espacio n-dimensional

Generaliza la ecuación para normalizar vectores en un espacio de cualquier dimensión. Un vector A (a, b, c, …), u = (a/z, b/z, c/z, …) donde z = (a^2 + b^2 + c^2 …)^(1/2).