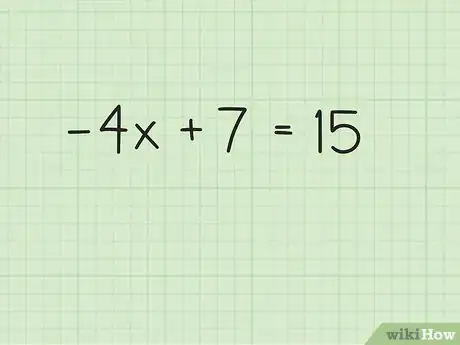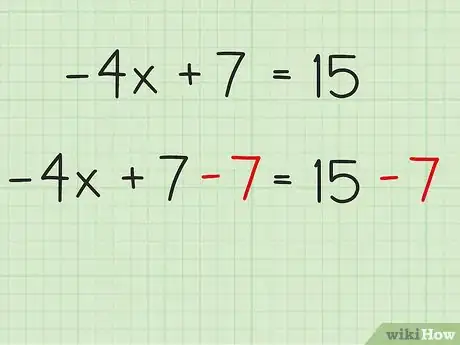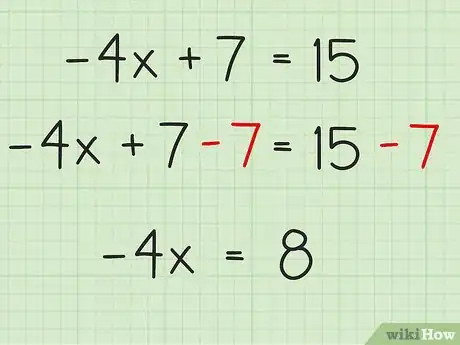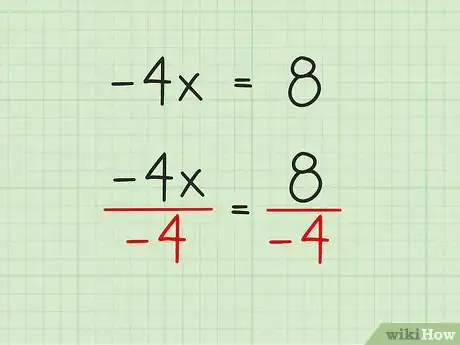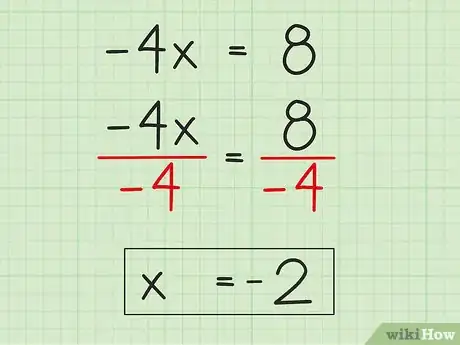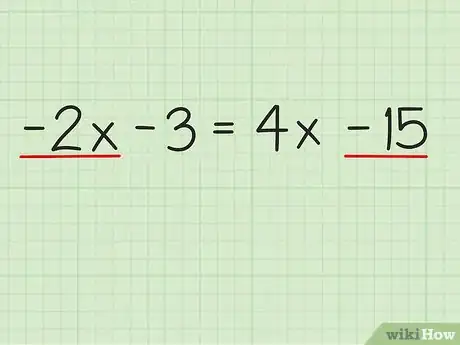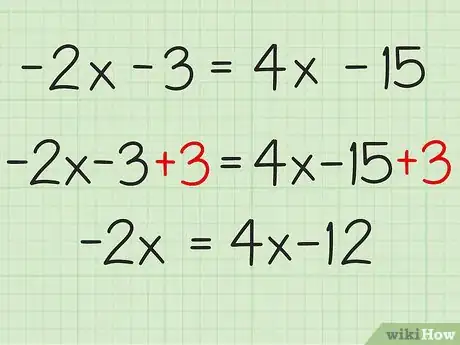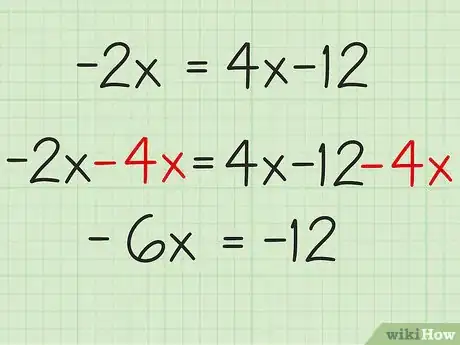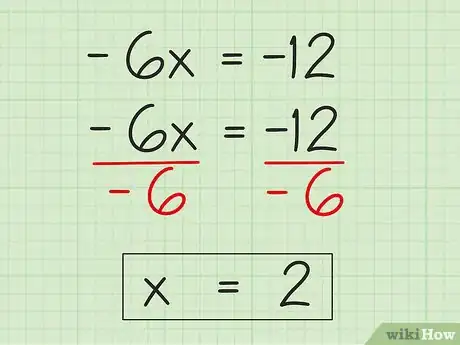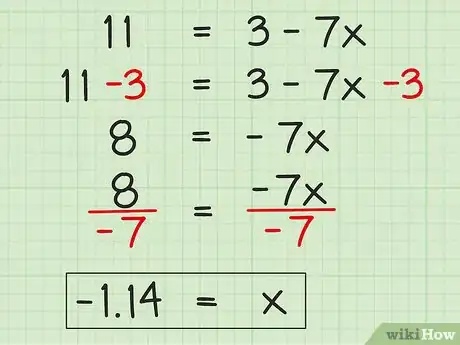Cómo resolver ecuaciones algebraicas de dos pasos

Información del autor

Las ecuaciones algebraicas de dos pasos son relativamente rápidas y sencillas; después de todo, solo deben tomar dos pasos. Para resolver una ecuación algebraica de dos pasos, todo lo que debes hacer es aislar la variable usando la adición, la sustracción, la multiplicación o la división. Si quieres saber cómo resolver ecuaciones algebraicas en una variedad de formas, solo sigue los pasos a continuación.

Método 1

Método 1 de 3:
Resolver ecuaciones con una variable

1
Escribe el problema. El primer paso para resolver una ecuación algebraica de dos pasos es simplemente escribir el problema para que puedas visualizar la solución. Supongamos que tenemos el siguiente problema: -4x + 7 = 15.
2
Decide si vas a usar la adición o sustracción para aislar el término de la variable. El siguiente paso es hallar una manera de dejar el "-4x" en un lado y mantener las constantes (números enteros) en el otro. Para hacerlo, deberás aplicar el "inverso aditivo" encontrando el opuesto de +7, que es -7. Sustrae 7 en ambos lados de la ecuación de modo que el "+7" en el lado del término de la variable se cancele. Solo escribe "-7" debajo del 7 en un lado y debajo del 15 en el otro para que la ecuación siga equilibrada.
- Recuerda la regla de oro del álgebra. Lo que hagas en un lado de una ecuación debes hacerlo también en el otro para mantener el equilibrio. Es por ello que a 15 se le sustrae 7. Solo sustraemos 7 una vez por lado, lo que explica la razón por la cual no se sustrae también 7 al -4x.
3
Suma o resta la constante en ambos lados de la ecuación. Esta operación completará el proceso de aislamiento del término de la variable. Restar 7 de +7 en el lado izquierdo de la ecuación no dejará una constante (es decir, quedará en 0) en dicho lado. Restar 7 de +15 en el lado derecho de la ecuación te dejará con 8. Por lo tanto, la nueva ecuación es -4x = 8.
- -4x + 7 = 15 =
- -4x = 8
4
Elimina el coeficiente de la variable mediante la división o multiplicación. El coeficiente es el número junto a la variable. En este ejemplo, el coeficiente es -4. Para eliminar el -4 en -4x, deberás dividir ambos lados de la ecuación entre -4. En este momento, la x se multiplica por -4, de modo que lo opuesto de esta operación es la división y tendrás que efectuarla en ambos lados.
- Una vez más, lo que hagas en la ecuación, debes hacerlo en ambos lados. Es por ello que ves el “÷ -4” dos veces.
5
Despeja la variable. Para hacerlo, divide el lado izquierdo de la oración, -4x entre -4 es igual a x. Divide el lado derecho de la ecuación, 8 entre -4 es igual a -2. Por lo tanto, x = -2. Has utilizado dos pasos (sustracción y división) para resolver este problema.

Anuncio

Método 2

Método 2 de 3:
Resolver ecuaciones con una variable en cada lado

1
Escribe el problema. El problema con el que trabajaremos es el siguiente: -2x - 3 = 4x - 15. Antes de proceder, asegúrate de que las variables sean las mismas. En este caso, "-2x" y "4x" tienen la misma variable, "x", así que puedes seguir adelante.
2
Mueve las constantes al lado derecho de la ecuación. Para hacerlo, deberás usar la adición o sustracción con el fin de eliminar la constante del lado izquierdo de la ecuación. La constante es -3, de modo que deberás tomar su opuesto, +3, y añadir esta constante a ambos lados de la ecuación.
- Añadir +3 al lado izquierdo de la ecuación, -2x -3, te dará (-2x -3) + 3 o -2x.
- Añadir +3 al lado derecho de la ecuación, 4x -15, te dará (4x - 15) +3 o 4x -12.
- Por lo tanto, (-2x - 3) +3 = (4x - 15) +3 = -2x = 4x - 12
- La nueva ecuación debe ser: -2x = 4x -12
3
Mueve las variables al lado izquierdo de la ecuación. Para hacerlo, simplemente deberás tomar "el opuesto" de "4x", que es "-4x", y sustraerlo en ambos lados de la ecuación. En el lado izquierdo, -2x - 4x = -6x y en el lado derecho, (4x -12) -4x = -12, de modo que la nueva ecuación debe ser: -6x = -12
- -2x - 4x = (4x - 12) - 4x = -6x = -12
4
Despeja la variable. Ahora que has simplificado la ecuación a -6x = -12, todo lo que debes hacer es dividir ambos lados de la ecuación entre -6 para aislar la variable x, que en este momento se multiplica por -6. En el lado izquierdo de la ecuación -6x ÷ -6 = x y en el lado derecho, -12 ÷ -6 = 2. Por lo tanto, x = 2.
- -6x ÷ -6 = -12 ÷ -6
- x = 2
Anuncio

Método 3

Método 3 de 3:
Otras maneras de resolver ecuaciones de dos pasos

1
Resuelve ecuaciones de dos pasos mientras mantienes la variable en el lado derecho. Puedes resolver una ecuación de dos pasos mientras mantienes la variable en el lado derecho, siempre y cuando la aísles. Tomemos el problema 11 = 3 - 7x. Para resolverlo, lo primero que harás será combinar las constantes al sustraer 3 en ambos lados de la ecuación. Luego deberás dividir ambos lados de la ecuación entre -7 para hallar x. Esta es la forma de hacerlo:
- 11 = 3 - 7x =
- 11 - 3 = 3 - 3 - 7x =
- 8 = - 7x =
- 8/-7 = -7/7x
- -8/7 = x o -1.14 = x
2
Resuelve una ecuación de dos pasos al multiplicar al final en lugar de dividir. El principio para resolver este tipo de ecuación es el mismo: utiliza la aritmética para combinar las constantes, aislar el término de la variable y luego aislar la variable fuera del término. Supongamos que tienes esta ecuación: x/5 + 7 = -3. Lo primero que debes hacer es sustraer 7, lo opuesto de -3, en ambos lados y luego multiplicar ambos lados por 5 para despejar x. Esta es la forma de hacerlo:
- x/5 + 7 = -3 =
- (x/5 + 7) - 7 = -3 - 7 =
- x/5 = -10
- x/5 * 5 = -10 * 5
- x = -50
Anuncio

Consejos

Al multiplicar o dividir dos números con signos distintos (p.ej. uno positivo y el otro negativo), el resultado siempre es negativo. Si ambos signos son iguales, entonces la solución es un número positivo.
Lee la pregunta con detenimiento.
Si no hay ningún número en frente de x, se asume que el término es 1x
Podría no haber una constante explícita en ambos lados. Si no hay un número al lado de x, asume que es x + 0.

Anuncio