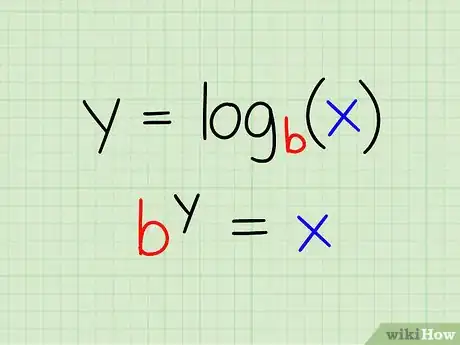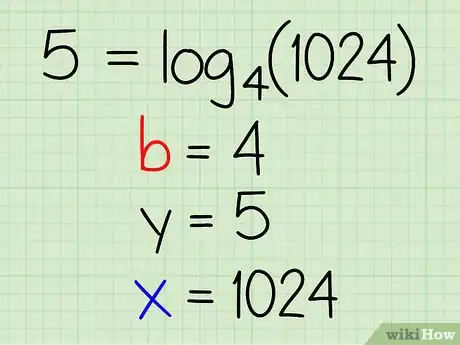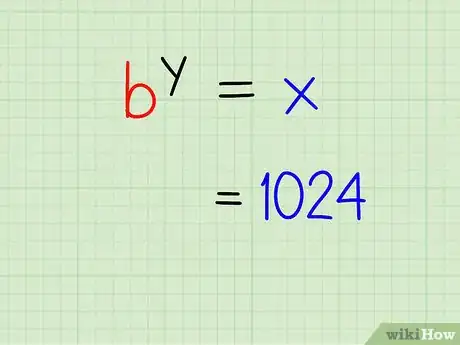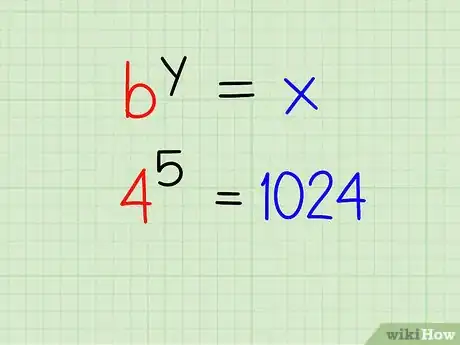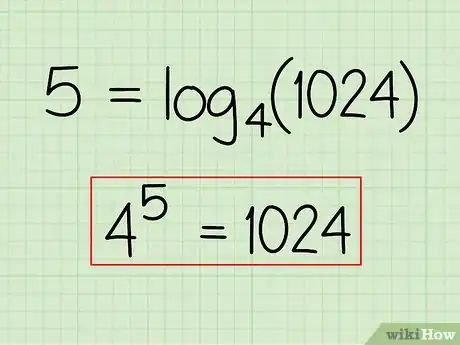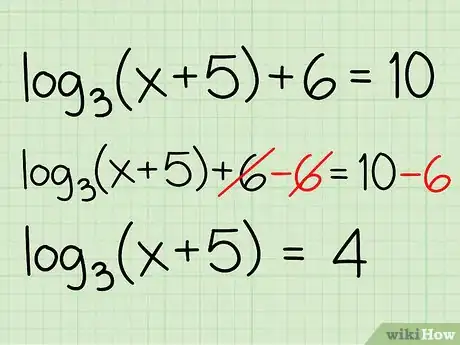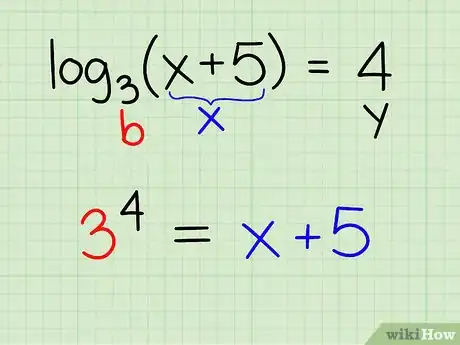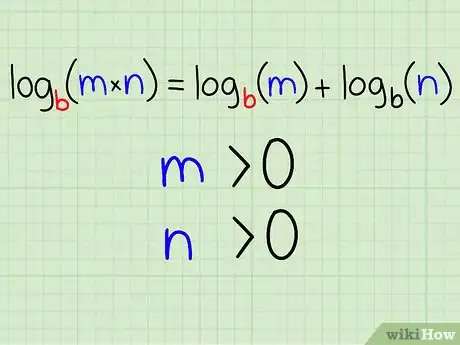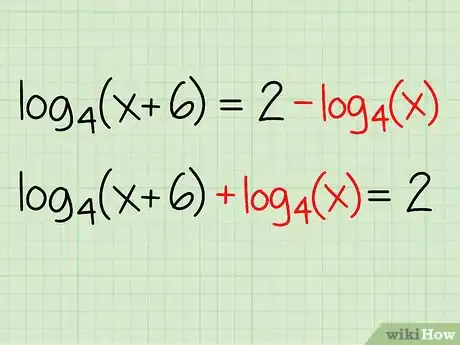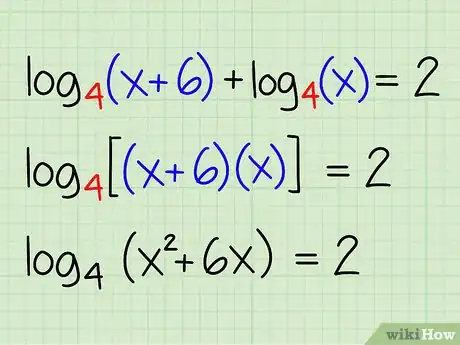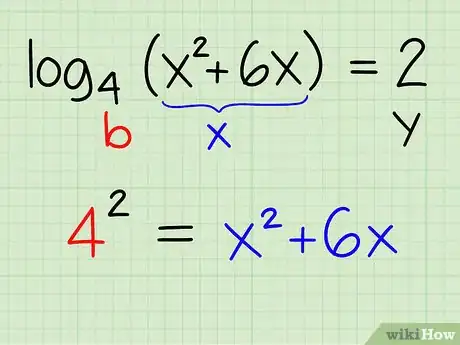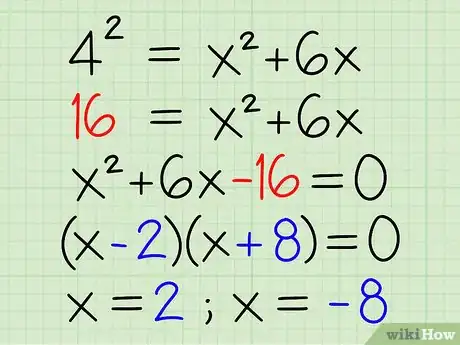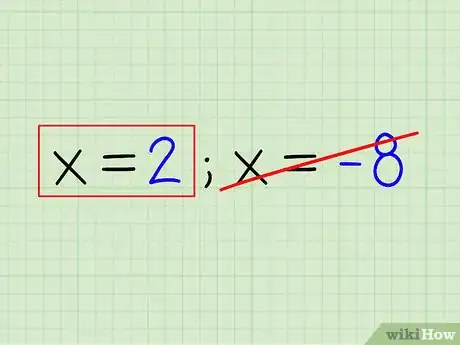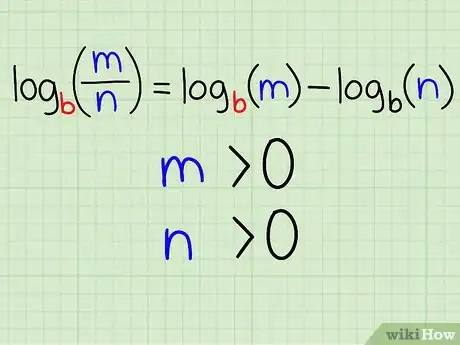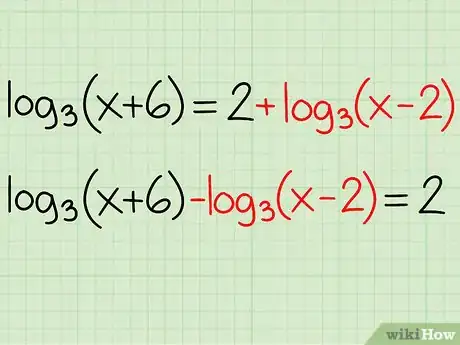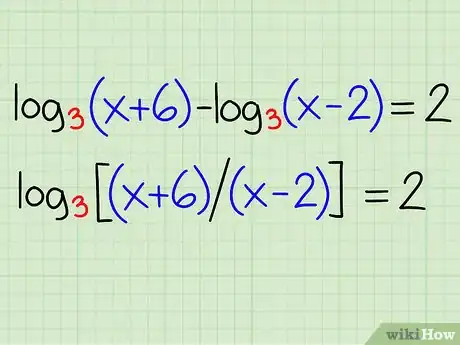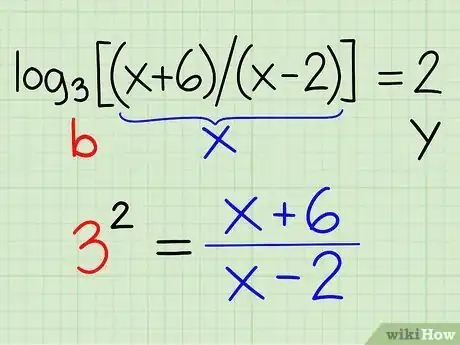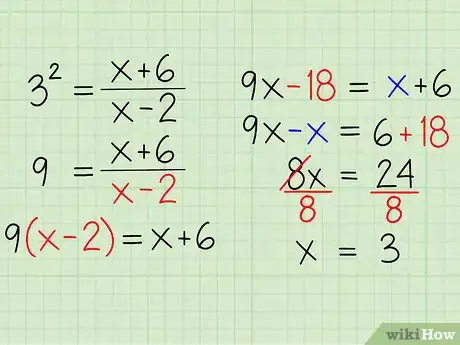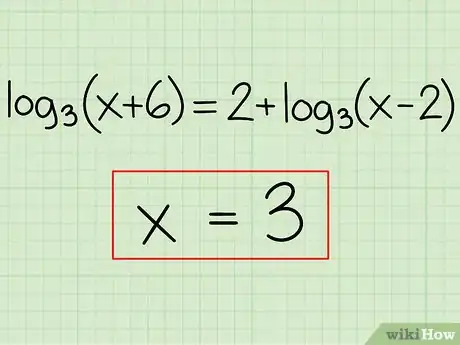X
wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, autores voluntarios han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 91 002 veces.
Los logaritmos pueden ser intimidantes, pero resolverlos es un proceso que se vuelve cada vez más fácil una vez que te hayas dado cuenta de que simplemente son otra forma de escribir una ecuación exponencial. Una vez que reescribes el logaritmo en una forma más familiar, podrás resolverlo como cualquier otra ecuación exponencial.
Pasos
Antes de empezar: aprende a expresar una ecuación logarítmica exponencialmente [1] [2]
-
1Debes conocer la definición de logaritmos. Antes de poder resolver logaritmos, debes entender que uno logaritmo es esencialmente otra forma de escribir una ecuación exponencial. La definición precisa es la siguiente:
-
y = logb (x)
- Si y sólo si: by = x
- Date cuenta que b es la base del logaritmo. Quizá también sea verdad que:
- b > 0
- b no es igual a 1
- En la misma ecuación, y es el exponente y x es la expresión exponencial a la que el logaritmo se iguala.
-
y = logb (x)
-
2Observa la ecuación. Cuando veas el la ecuación del problema, identifica la base (b), el exponente (y) y la expresión exponencial (x).
-
Ejemplo: 5 = log4(1024)
- b = 4
- y = 5
- x = 1024
-
Ejemplo: 5 = log4(1024)
-
3Mueve la expresión exponencial a un lado de la ecuación. Fija el valor de tu expresión exponencial, x, a un lado del signo igual.
- Ejemplo: 1024 = ?
-
4Aplica el exponente a la base. Debes multiplicar el valor de la base, b, por sí mismo la cantidad de veces indicadas por el exponente y.
-
Ejemplo: 4 * 4 * 4 * 4 * 4 = ?
- También puedes escribir esto como: 45
-
Ejemplo: 4 * 4 * 4 * 4 * 4 = ?
-
5Reescribe la respuesta final. Debes poder reescribir el logaritmo como una ecuación exponencial. Verifica que tu respuesta sea la correcta asegurándote de que ambos lados de la ecuación sean iguales.
- Ejemplo: 45 = 1024
Anuncio
Método 1
Método 1 de 3:Método 1: Resuelve para X
Método 1
-
1Aísla el logaritmo. Utiliza operaciones inversas para mover cualquier parte de la ecuación que no sea parte del logaritmo al otro lado de la ecuación.
-
Ejemplo: log3(x + 5) + 6 = 10
- log3(x + 5) + 6 - 6 = 10 - 6
- log3(x + 5) = 4
-
Ejemplo: log3(x + 5) + 6 = 10
-
2Reescribe la ecuación de forma exponencial. Utiliza tus conocimientos sobre la relación entre los logaritmos y las ecuaciones exponenciales para simplificar el logaritmo y escribir la ecuación de forma más simple.
-
Ejemplo:log3(x + 5) = 4
- Compara esta ecuación con la definición [y = logb (x)] y podrás concluir que: y = 4; b = 3; x = x + 5
- Reescribe la ecuación para que: by = x
- 34 = x + 5
-
Ejemplo:log3(x + 5) = 4
-
3Resuelve para x. Una vez que hayas simplificado el problema en una ecuación exponencial básica, podrás resolverlo como cualquier otra ecuación.
-
Ejemplo: 34 = x + 5
- 3 * 3 * 3 * 3 = x + 5
- 81 = x + 5
- 81 - 5 = x + 5 - 5
- 76 = x
-
Ejemplo: 34 = x + 5
-
4Escribe la respuesta final. La respuesta que obtuviste cuando resolviste para x es la solución al logaritmo original.
- Ejemplo: x = 76
Anuncio
Método 2
Método 2 de 3:Método 2: Resuelve para X con la regla del producto[3]
[4]
Método 2
-
1Debes conocer la regla de producto de logaritmos. Esta primera propiedad de los logaritmos, conocida como “regla del producto”, dice que el logaritmo de un producto es igual a la suma de los logaritmos de ambos factores. Escrita en forma de ecuación se ve así:
- logb(m * n) = logb(m) + logb(n)
- Debes darte cuenta que lo siguiente siempre debe ser verdad:
- m > 0
- n > 0
-
2Aísla el logaritmo a un lado de la ecuación. Utiliza operaciones inversas para mover las partes de la ecuación de modo que los logaritmos estén de un lado mientras que todos los otros elementos estén del otro lado de la ecuación.
-
Ejemplo: log4(x + 6) = 2 - log4(x)
- log4(x + 6) + log4(x) = 2 - log4(x) + log4(x)
- log4(x + 6) + log4(x) = 2
-
Ejemplo: log4(x + 6) = 2 - log4(x)
-
3Aplica la regla del producto. Si hay una suma de logaritmos en la ecuación, puedes utilizar la regla del producto para combinarlos en uno solo.
-
Ejemplo: log4(x + 6) + log4(x) = 2
- log4[(x + 6) * x] = 2
- log4(x2 + 6x) = 2
-
Ejemplo: log4(x + 6) + log4(x) = 2
-
4Vuelve a escribir la ecuación de forma exponencial. Recuerda que un logaritmo es simplemente otra manera de escribir una ecuación exponencial. Utiliza esta definición para reescribirla en una forma más fácil.
-
Ejemplo: log4(x2 + 6x) = 2
- Si comparas esta ecuación con la definición [y = logb (x)] puedes concluir que: y = 2; b = 4 ; x = x2 + 6x
- Reescribe la ecuación de modo que: by = x
- 42 = x2 + 6x
-
Ejemplo: log4(x2 + 6x) = 2
-
5Resuelve para x. Ahora que la ecuación tiene una forma estándar de una ecuación exponencial, utiliza tus conocimientos sobre este tipo de ecuaciones para resolver para x como normalmente lo harías.
-
Ejemplo: 42 = x2 + 6x
- 4 * 4 = x2 + 6x
- 16 = x2 + 6x
- 16 - 16 = x2 + 6x - 16
- 0 = x2 + 6x - 16
- 0 = (x - 2) * (x + 8)
- x = 2; x = -8
-
Ejemplo: 42 = x2 + 6x
-
6Escribe la respuesta. En este punto ya debes tener la solución para la ecuación. Escríbela en el espacio correspondiente.
- Ejemplo: x = 2
- Debes darte cuenta de que no existe una solución negativa para un logaritmo, así que puedes descartar x - 8 como solución.
Anuncio
Método 3
Método 3 de 3:Método 3: Resuelve para X con la regla del cociente[5]
Método 3
-
1Debes conocer la regla del cociente. De acuerdo a la segunda propiedad de logaritmos, conocida como la “regla del cociente”, puedes escribir el logaritmo de un cociente como la resta del logaritmo del denominador menos la resta del logaritmo del numerador. Escrito en forma de ecuación se ve así:
- logb(m / n) = logb(m) - logb(n)
- También debes saber que lo siguiente debe ser verdad:
- m > 0
- n > 0
-
2Aísla el logaritmo a un lado de la ecuación. Antes de que puedas resolver el logaritmo, debes cambiar todos los logaritmos de la ecuación a un solo lado del signo igual. Debes cambiar todas las otras partes de la ecuación al lado opuesto. Utiliza operaciones inversas para lograrlo.
-
Ejemplo: log3(x + 6) = 2 + log3(x - 2)
- log3(x + 6) - log3(x - 2) = 2 + log3(x - 2) - log3(x - 2)
- log3(x + 6) - log3(x - 2) = 2
-
Ejemplo: log3(x + 6) = 2 + log3(x - 2)
-
3Aplica la regla del cociente. Si hay una resta de dos logaritmos en la ecuación, puedes utilizar la regla del cociente para combinarlos como un solo logaritmo.
-
Ejemplo: log3(x + 6) - log3(x - 2) = 2
- log3[(x + 6) / (x - 2)] = 2
-
Ejemplo: log3(x + 6) - log3(x - 2) = 2
-
4Reescribe la ecuación en su forma exponencial. Ahora que solo hay un logaritmo en la ecuación, utiliza la definición de logaritmos para reescribir la ecuación en su forma exponencial, eliminando así el logaritmo.
-
Ejemplo: log3[(x + 6) / (x - 2)] = 2
- Si comparas esta ecuación con la definición [y = logb (x)]puedes concluir que: y = 2; b = 3; x = (x + 6) / (x - 2)
- Reescribe la ecuación de manera que: by = x
- 32 = (x + 6) / (x - 2)
-
Ejemplo: log3[(x + 6) / (x - 2)] = 2
-
5Resuelve para x. Ahora que la ecuación está en forma exponencial, debes poder resolver para x como normalmente lo harías.
-
Ejemplo: 32 = (x + 6) / (x - 2)
- 3 * 3 = (x + 6) / (x - 2)
- 9 = (x + 6) / (x - 2)
- 9 * (x - 2) = [(x + 6) / (x - 2)] * (x - 2)
- 9x - 18 = x + 6
- 9x - x - 18 + 18 = x - x + 6 + 18
- 8x = 24
- 8x / 8 = 24 / 8
- x = 3
-
Ejemplo: 32 = (x + 6) / (x - 2)
-
6Escribe la respuesta final. Vuelve a revisar todos tus pasos. Una vez que te sientas seguro de que tienes la respuesta correcta, escríbela.
- Ejemplo: x = 3
Anuncio
Referencias
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut43_logfun.htm#logdef
- ↑ http://www.mathsisfun.com/algebra/logarithms.html
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut46_logeq.htm
- ↑ http://dl.uncw.edu/digilib/mathematics/algebra/mat111hb/eandl/equations/equations.html
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut44_logprop.htm
Acerca de este wikiHow
Anuncio