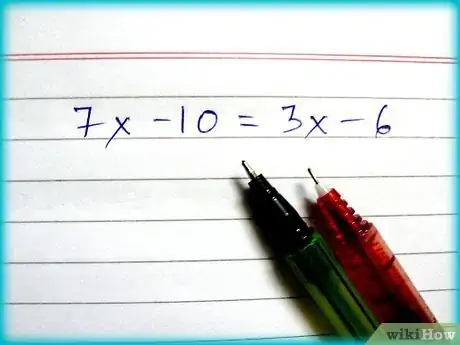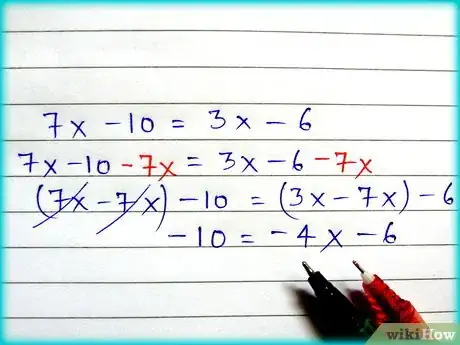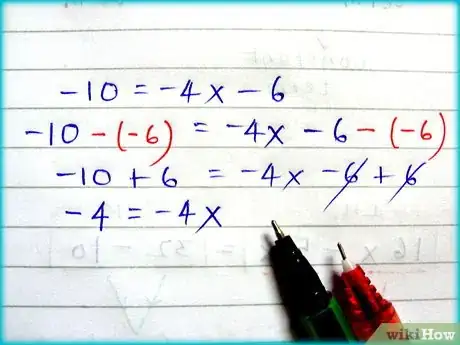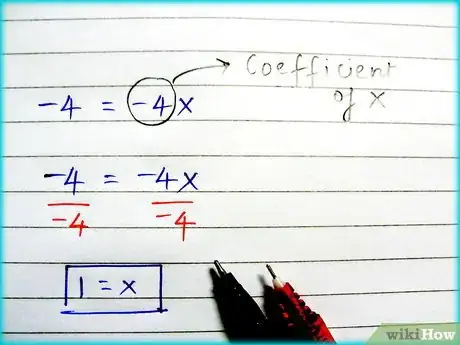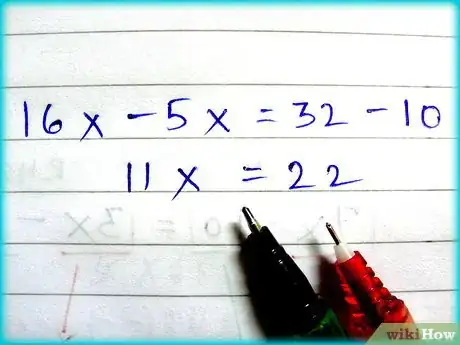X
wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 9 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 154 779 veces.
Necesitas averiguar a qué equivale “x” si tienes un problema como este 7x – 10 = 3x + 6. Este tipo de ecuación es llamada ecuación lineal, y usualmente tiene solo una variable. Este artículo te guiará por los simples pasos.
Pasos
Método 1
Método 1 de 2:Comenzando con las variables en lados opuestos
Método 1
-
1Mira tu problema: 7x – 10 = 3x – 6. Una ecuación lineal simple pueda que luzca así:
-
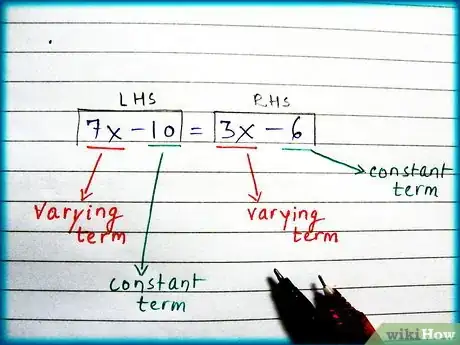
2Revisa la ecuación y halla los términos variables y constantes. Los términos variables son números como “7x” ó “3x” ó “6y” ó “10z”, donde el número cambia en función de lo que vaya junto a la variable o letra. Los términos constantes son números como “10” ó “6” ó “30”, donde el número nunca cambia.
- Usualmente, las ecuaciones no vendrán con los términos constantes y variables alineados en lados separados. En el ejemplo presentado, el lado izquierdo contiene tanto términos variables como constantes, del mismo modo que el lado derecho.
-
3Prepárate a mover los números de tal manera que los términos variables estén en un lado y los términos constantes estén en el otro lado, así: 16x – 5x = 32 – 10 (esta ecuación es resuelta en el ejemplo 2). Para hacer esto, quizá tengas que restar o sumar los números que quieras mover de ambos lados. En el siguiente paso, verás cómo hacer esto en el ejemplo 1.
- La ecuación “16x – 5x = 32 – 10” sí tiene todos los términos variables en un lado (en el izquierdo), mientras que todos los términos constantes están en el otro lado (el derecho).
-
4Mueve los términos variables a un lado de la ecuación. No importa hacia qué lado los muevas.
- En el ejemplo 1, la ecuación 7x – 10 = 3x - 6 puede ser reorganizada eligiendo restar ya sea (7x) o (3x) de ambos lados. Si eliges restar 7x, tendrías:
(7x - 7x) - 10 = (3x - 7x) - 6.
-10 = -4x - 6
- En el ejemplo 1, la ecuación 7x – 10 = 3x - 6 puede ser reorganizada eligiendo restar ya sea (7x) o (3x) de ambos lados. Si eliges restar 7x, tendrías:
-
5Luego, trae todos los términos constantes hacia el otro lado de la ecuación. En otras palabras, mueve los términos constantes de forma que estén en el lado opuesto de donde están los términos variables en la ecuación.
- Vemos que -6 debe ser restado de ambos lados:
-10 - (-6) = -4x - 6 - (-6).
-4 = -4x
- Vemos que -6 debe ser restado de ambos lados:
-
6Finalmente, para encontrar el valor de x, simplemente divide ambos lados por el “coeficiente de x”. El coeficiente de x (o y, o z, o cualquier letra) es el número frente al término variable.
- El coeficiente de x en -4x es -4. Así que divide ambos lados por -4 para obtener el valor de x = 1.
- Nuestra respuesta a la ecuación 7x - 10 = 3x - 6 es x = 1. Puedes verificar esta respuesta colocando el número 1 junto a cada variable “x” y viendo si ambos lados de la ecuación resultan en el mismo número:
7(1) - 10 = 3(1) - 6
7 - 10 = 3 - 6
-3 = -3
Anuncio
Método 2
Método 2 de 2:Comenzando con las variables en un lado
Método 2
-
1Ten en cuenta que a veces, los términos variables y los términos constantes estarán separados. A veces, la mitad del trabajo ya estará hecho para ti. Tendrás todos los términos variables en un lado y todos los términos constantes en el lado opuesto. Si este es el caso, todo lo que tienes que hacer es lo siguiente.
-
2Simplifica ambos lados. Para la ecuación 16x - 5x = 32 - 10, solo tenemos que restar los números uno del otro.
-
3Luego, divide ambos lados por el coeficiente de x. Recuerda que el coeficiente de x es el número frente al término variable.
- En este ejemplo, el coeficiente de x en 11x es 11. Esta división es 11x ÷ 11 = 22 ÷ 11 para obtener x = 2. La respuesta a la ecuación 16x - 5x = 32 - 10 es x = 2
Anuncio
Advertencias
- ¿Por qué hacerlo de esta manera? Tratar de dividir esto:
4x - 10 = - 6 así 4x/4 - 10/4 = -6/4 crea esto x - 10/4 = -6/4, con muchas fracciones con las cuales lidiar, y esto no es tan fácil de resolver; es por esto que, “simplificar” es una buena razón por la cual debes colocar todos los términos variables de un lado y todos los términos constantes del lado opuesto.
Anuncio
Acerca de este wikiHow
Anuncio