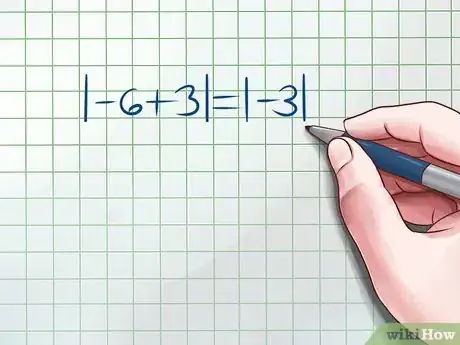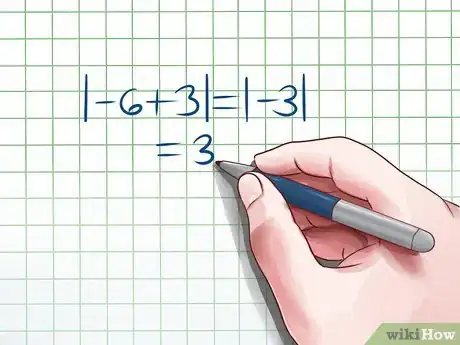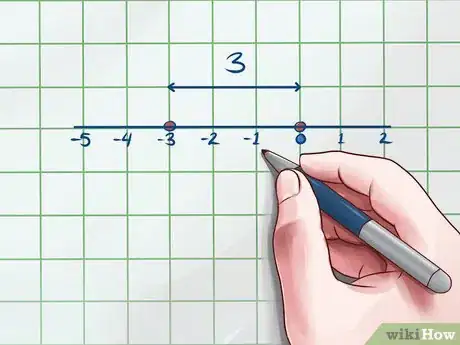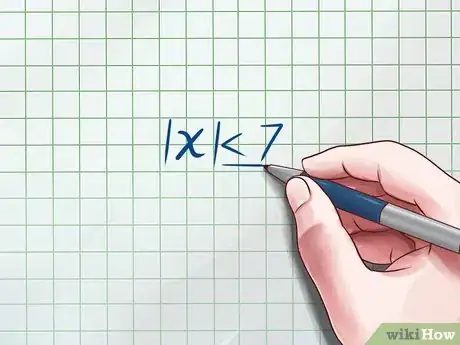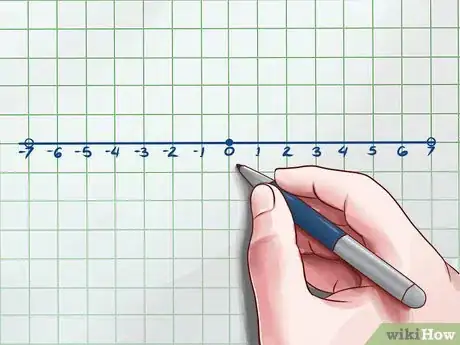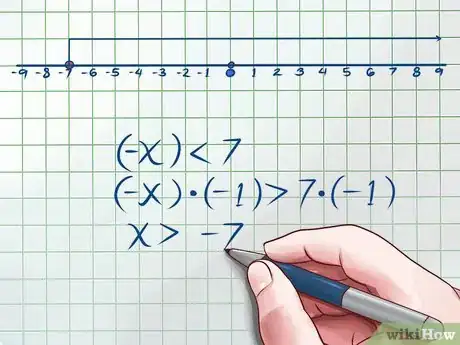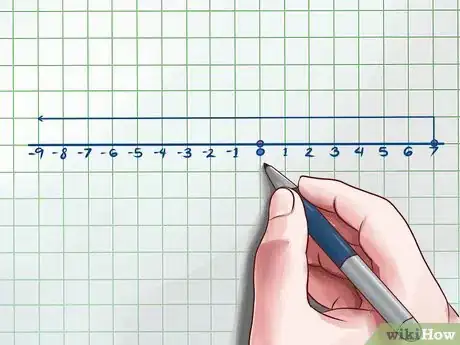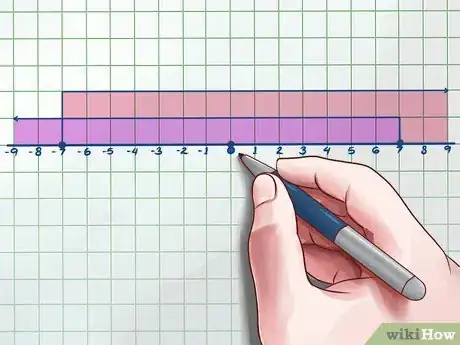Cómo simplificar valores absolutos

Información del autor

El valor absoluto es una expresión de la distancia de un número con respecto al 0. Está denotado por dos barras verticales a cada lado del número, variable o expresión. A cualquier cosa dentro de las barras del valor absoluto se le conoce como “argumento”. Las barras del valor absoluto no funcionan como paréntesis o corchetes, así que es crucial que las utilices apropiadamente.

Método 1

Método 1 de 2:
Simplificación cuando el argumento es un número

1
Determina la expresión. Simplificar un argumento numérico es un proceso relativamente fácil. Debido a que el valor absoluto representa la distancia entre tu número y el 0, la respuesta siempre será positiva. Empieza por resolver cualquier operación dentro de las barras del valor absoluto para determinar la expresión.
- Por ejemplo, digamos que quieres simplificar el valor absoluto de la expresión “-6+3”. Debido a que toda la expresión está dentro de las barras del valor absoluto, primero haz la suma. El paso siguiente es simplificar el valor absoluto de “-3”.
2
Simplifica el valor absoluto. Una vez que hayas realizado todas las operaciones que haya dentro de las barras del valor absoluto, podrás simplificar el argumento. Cualquier número que tengas como argumento, sea positivo o negativo, representa la distancia del 0, así que la respuesta es ese número y es positiva.
- En el ejemplo anterior, el valor absoluto simplificado es 3. Esto es cierto porque la distancia entre 0 y -3 es 3.
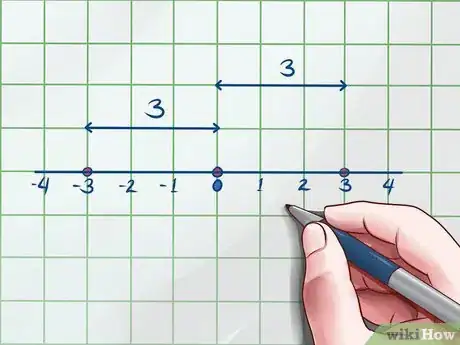
3
Utiliza una recta numérica. Tienes la opción de verificar tu respuesta utilizando una recta numérica. Este paso puede ayudarte a visualizar los valores absolutos y revisar tu trabajo.
- Para el ejemplo anterior, la recta numérica debe verse así:

Método 2

Método 2 de 2:
Simplificación cuando el argumento incluye una variable

1
Trabaja con el argumento que sea una variable. Si tu argumento es una variable por su cuenta que está igualada a un número, entonces la simplificación es muy fácil. Debido a que el valor absoluto representa una distancia desde el 0, tu variable puede ser el número positivo al que es igual o podría ser la versión negativa de ese número. No hay como saber cuál es la respuesta, así que debes incluir ambas posibilidades en la solución.
- Por ejemplo, digamos que sabes que el valor absoluto de una variable X es igual a 3. No tienes cómo saber si X es positivo o negativo. Lo que estás buscando es un número cuya distancia del 0 sea 3. Por lo tanto, la solución es 3 o -3.
- Si este es el tipo de argumento que debes simplificar, detente aquí. Tu trabajo está terminado, sin embargo, si tu argumento tiene una inecuación, continúa.
2
Debes reconocer las inecuaciones dentro de valores absolutos. Si, por el contrario, te dan un argumento que tiene un variable y está expresada como una inecuación, debes realizar unos pasos más. Interpreta estas inecuaciones cómo si te estuvieran pidiendo que encuentres todos los números posibles.
- Por ejemplo, digamos que tienes la siguiente inecuación. Puedes interpretar esto como “todos los números cuyos valores absolutos sean menores a 7”. En otras palabras, busca todos los números cuya distancia del 0 sea 7, excluyendo al 7. Debes notar que la inecuación dice “menor a” no “menor o igual a”. Si dijera “menor o igual a”, entonces si debes incluir al 7.
3
Grafica una recta numérica. Lo primero que debes hacer cuando encuentres una inecuación dentro de un valor absoluto es graficar la recta numérica. Coloca los puntos correspondientes a los números con los que vas a trabajar.
- En el ejemplo anterior, la línea se vería así: El círculo abierto indica que el número está excluido del resultado final. Recuerda: si la inecuación dijera “mayor o igual a” o “menor o igual a”, entonces si debes incluir los números en la solución. En ese caso, los círculos deben ser sólidos.
4
Considera los números del lado izquierdo de la línea del número. Debido a que no sabes si tu variable es positiva o negativa, realmente estás viendo dos rangos de números posibles: aquellos en el lado izquierda de la recta numérica y aquellos al lado derecho. Primero, considera los números del lado izquierda. Haz que la variable sea negativa y convierte las barras de valores absolutos en paréntesis. Resuelve.
- En el ejemplo anterior, debes convertir las barras del valor absoluto para mostrar que (-X) es menor que 7. Multiplica ambos lados de la inecuación por -1. Debes saber que cuando multiplicas una inecuación por un número negativo, debes cambiar el signo de la inecuación (de “menor a” a “mayor a” o viceversa). La inecuación debe verse así: Ahora sabes que para el lado izquierdo de la recta numérica, X será mayor que -7. En la recta numérica, esto se vería así:
5
Considera los números en el lado derecho de la recta numérica. Ahora puedes ver los números del otro rango, aquellos que son positivos. Esto es incluso más simple: haz que la variable sea positiva convirtiendo las barras de valor absoluto en paréntesis.
- En el ejemplo anterior, lo que harías es convertir las barras de valor absoluto en paréntesis para mostrar que (X) es menor que 7. No necesitas hacer nada más en este paso. En la recta numérica, esto se ve así:
6
Busca la intersección de los dos intervalos. Una vez que has considerado ambos lados, debes determinar dónde se interponen las soluciones. Dibuja ambos intervalos en la misma recta numérica para obtener el resultado.
- En el ejemplo anterior, lo que harías es resaltar los valores mayores a -7 y menores a 7 (a excepción del -7 y 7). Estas son las soluciones.

Consejos

Recuerda que las barras de valor absoluto son diferentes a los paréntesis o corchetes. Puedes convertirlas en paréntesis en el paso apropiado pero no necesariamente significan lo mismo.