Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
En este artículo, hay 7 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 91 676 veces.
El sistema de números binarios funciona de forma similar al sistema decimal que se utiliza habitualmente, con la excepción de que se trata de un sistema de base 2, es decir, se compone de solo dos dígitos: 1 y 0.[1] Este sistema es la base del funcionamiento de las computadoras.[2] Básicamente, el código binario emplea 1 y 0 para activar o desactivar determinados procesos.[3] Es posible sumar los números binarios tal como se hace con los números decimales y, si bien el proceso es algo familiar, acostumbrarte al sistema de base 2 puede ser una tarea confusa. Por ende, te será de utilidad saber muy bien la forma en que el valor posicional funciona en el sistema binario antes de sumar estos números.
Pasos
Parte 1
Parte 1 de 3:Entender el sistema binario
-
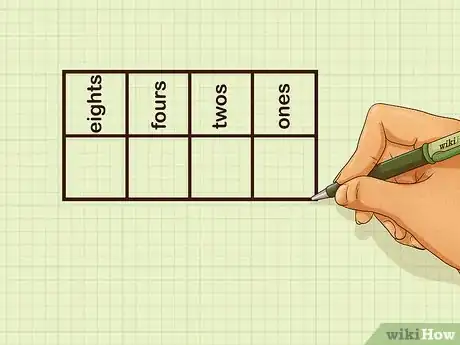
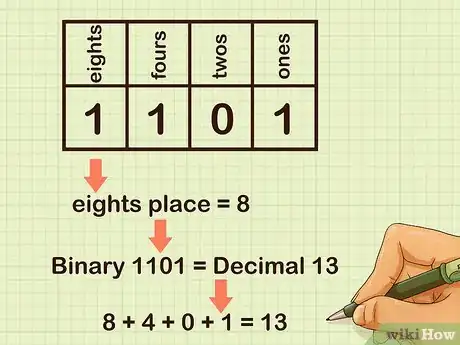
1Dibuja un cuadro de valores posicionales con dos filas y cuatro columnas. Etiqueta a cada columna con un valor posicional. El sistema binario solo emplea dos números, de modo que en lugar de usar unidades, decenas, centenas y milésimas como en el sistema decimal, este emplea unos, dos, cuatros y ochos.[4] El lugar de los unos se ubica en la columna del extremo derecho mientras que el de los ochos se encuentra en la del izquierdo.
- Continúa con el cuadro de valores posicionales. Cada valor posicional se determina con un exponente de base 2.[5]
Por ejemplo:
- Continúa con el cuadro de valores posicionales. Cada valor posicional se determina con un exponente de base 2.[5]
Por ejemplo:
-
2Escribe un número binario al azar en la fila inferior del cuadro. En el sistema binario, los únicos dígitos que se utilizan son y .[6]
- Por ejemplo, puedes escribir un 1 en el lugar de los ochos, otro en el de los cuatros, un 0 en el de los dos, y otro 1 en el de los unos: 1101.
-
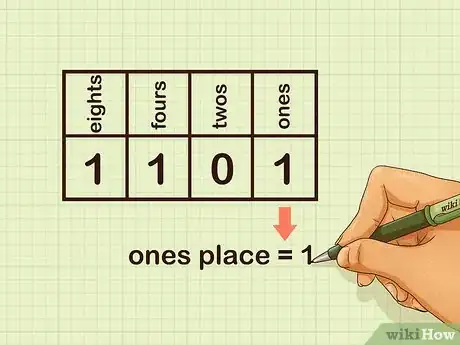
3Interpreta el lugar de los unos. Si hay un 0 en el lugar de los unos, significa que el valor es 0. Si hay un uno, el valor será 1.
- Por ejemplo, en el caso del número binario 1101, hay un 1 en el lugar de los unos, de modo que el valor es 1. Por consiguiente, el número binario 1 es equivalente al número decimal 1.
-
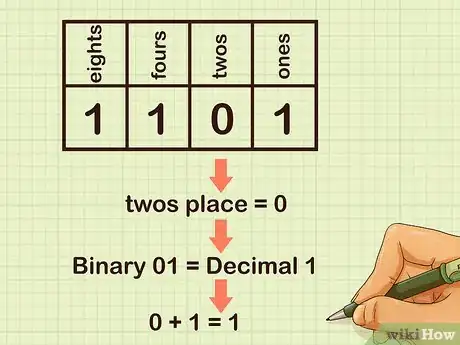
4Interpreta el lugar de los dos. Si hay un 0 en el lugar de los dos, significa que el valor es 0. Si hay un uno, el valor será 2.
- Por ejemplo, en el caso del número binario 1101, hay un 0 en el lugar de los dos, de modo que el valor es 0. Por consiguiente, el número binario 01 es equivalente al número decimal 1, pues hay 0 dos y solo 1 uno: 0 + 1 = 1.
-
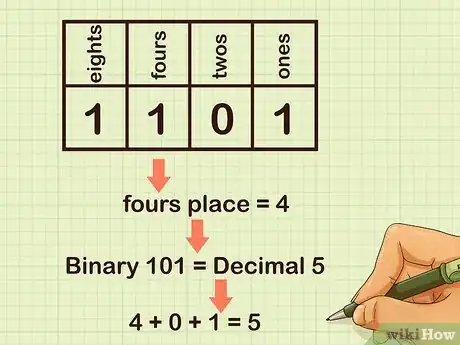
5Interpreta el lugar de los cuatros. Si hay un 0 en el lugar de los cuatros, el valor será 0. Por el contrario, si hay un 1 en este lugar, el valor será 4.
- Por ejemplo, en el caso del número binario 1101, hay un 1 en el lugar de los cuatros, de modo que el valor es 4. Por consiguiente, el número binario 101 es equivalente al número decimal 5, pues hay 1 cuatro, 0 dos y 1 uno: 4 + 0 + 1 = 5.
-
6Interpreta el lugar de los ochos. Si hay un 0 en el lugar de los ochos, entonces el valor será 0. Por el contrario, si hay un 1, el valor será 8.
- Por ejemplo, en el caso del número binario 1101, hay un 1 en el lugar de los ochos, de modo que el valor es 8. Por consiguiente, el número binario 101 es equivalente al número decimal 13, pues hay 1 ocho, 1 cuatro, 0 dos y 1 uno: 8 + 4 + 0 + 1 = 13.
Parte 2
Parte 2 de 3:Sumar números binarios utilizando el valor posicional
-
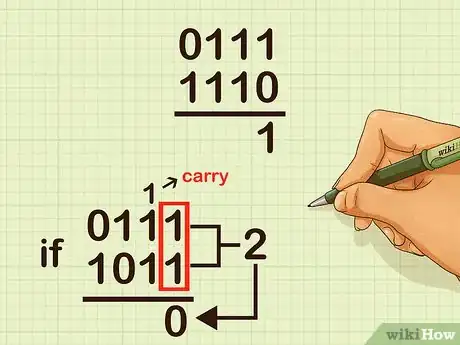
1Organiza el problema en vertical y luego suma los dígitos en el lugar de las unidades. Debido a que solo sumarás dos dígitos, la posible suma será 0, 1 o 2. Si la suma da como resultado 0, escribe 0 en el lugar de los unos. Si la suma da como resultado 1, escríbelo en el lugar de los unos. Si la suma es 2, escribe un 0 en el lugar de los unos y lleva un 1 a la columna de los dos.[7]
- Por ejemplo, si vas a sumar los números 0111 y 1110, en la columna de los unos sumarías 1 uno más 0 unos, lo que da como resultado 1. Por lo tanto, deberás colocar un 1 en la columna de los unos.
-
2Suma los dígitos en el lugar de los dos. La posible suma es 0, 1, 2 o 3 (si llevaste un número del lugar de los unos). Si la suma da como resultado 0, escríbelo en el lugar de los dos. Si la suma es un 1, escríbelo en dicho lugar. Asimismo, si la suma es 2, escribe un 0 en el lugar de los dos y lleva un 1 hacia la columna de los cuatros. Si la suma es 3, escribe un 1 en el lugar de los dos, y luego lleva un 1 a la columna de los cuatros (3 dos = 6 = 1 dos y 1 cuatro).
- Por ejemplo, si vas a sumar los números 0111 y 1110, en la columna de los dos deberías sumar 1 dos más 1 dos = 2 dos = 4. Por lo tanto, debes colocar un 0 en la columna de los dos y llevar un 1 hacia la columna de los cuatro.
-
3Suma los dígitos en el lugar de los cuatros. La posible suma es 0, 1, 2 o 3 (si llevaste un número del lugar de los dos). Si la suma da como resultado 0, escríbelo en el lugar de los cuatros. Si la suma es 1, escríbelo en dicho lugar. Si la suma es 2, escribe un 0 en el lugar de los cuatros y lleva un 1 hacia la columna de los ochos. Si la suma es 3, escribe un 1 en el lugar de los cuatros y lleva un 1 hacia la columna de los ochos (3 cuatros = 12 = 1 cuatro y 1 ocho).
- Por ejemplo, si vas a sumar los números 0111 y 1110, en la columna de los cuatros deberías sumar 1 cuatro más 1 cuatro más 1 cuatro = 3 cuatros = 12. Por lo tanto, debes colocar un 1 en la columna de los cuatros y llevar un 1 hacia la columna de los ochos.
-
4Sigue sumando los dígitos en cada valor posicional del número hasta que obtengas la respuesta final. Para hacer las cosas más sencillas, recuerda que 0 = 0, 1 = 1, 2 = 10 y 3 = 11.
- Por ejemplo, si vas a sumar los números 0111 y 1110, sumarías 2 ochos en la columna de los ochos debido a que llevaste un número desde la columna de los cuatros. En el caso de una suma de 2, coloca un 0 en la columna de los ochos y lleva un 1 hacia la columna de los dieciséis. Como ya no hay más números en esta última columna, solo baja ese 1 hacia la respuesta final. Por lo tanto, 0111 + 1110 = 10101.
Parte 3
Parte 3 de 3:Sumar varios números binarios al emparejar los 1
-
1Organiza el problema de manera vertical. Encierra en un círculo los pares de 1 (dígitos) en la columna de los unos. Recuerda que, en el sistema binario, esta columna se ubica en el extremo derecho.
- Por ejemplo, si vas a sumar 1010 + 1111 + 1011 + 1110, debes encerrar en un círculo un par de 1.
-
2Interpreta la columna de los unos. Por cada par de 1, lleva uno hacia la columna de los dos. SI solo hay un 1 o si solo queda uno después de haber encerrado en un círculo otros pares, escríbelo como respuesta en el lugar de los unos. Si no hay ningún 1, coloca un 0 en el lugar de los unos.[8]
- Por ejemplo, como encerraste en un círculo a un par de 1, debes llevar un 1 hacia la columna de los dos y dejar un 0 en la columna de los unos a modo de repuesta.
-
3Encierra en un círculo los pares de 1 en la columna de los dos. No olvides incluir los dígitos que llevaste de la columna de los unos.
- Por ejemplo, si vas a sumar 1010 + 1111 + 1011 + 1110, debes encerrar en un círculo dos pares de 1 y dejar uno suelto.
-
4Interpreta la columna de los dos. Por cada par de 1, lleva uno hacia la columna de los cuatros y deja un 0 en el lugar de los dos. Si solo hay un 1 o si hay un 1 sobrante después de haber encerrado en un círculo los pares de 1, coloca un 1 en la columna de los dos a modo de respuesta. Si no queda ningún 1, coloca un 0 en la columna de los unos.
- Por ejemplo, como encerraste en un círculo 2 pares de 1 y queda un 1 suelto, debes llevar un 1 hacia la columna de los cuatros dos veces y deja un 1 en la columna de los dos como respuesta.
-
5Encierra en un círculo los pares de 1 en la columna de los cuatros. Recuerda incluir los dígitos que llevaste hacia la columna de los dos.
- Por ejemplo, si vas a sumar 1010 + 1111 + 1011 + 1110, debes encerrar en un círculo dos pares de 1, debido a que llevaste el 1 dos veces hacia la columna de los dos.
-
6Interpreta la columna de los cuatros. Por cada par de 1, lleva uno hacia la columna de los ochos. Si queda un 1 sobrante, no olvides ponerlo en el lugar de los cuatros. Por otra parte, si no queda ningún 1, coloca un 0 en dicho lugar.
- Por ejemplo, como encerraste en un círculo a dos pares de 1 sin que quede alguno suelto, debes llevar un 1 hacia la columna de los ochos dos veces y colocar un 0 en la columna de los cuatros.
-
7Sigue encerrando en círculos los pares de 1 por cada valor posicional. Recuerda llevar un 1 hacia la siguiente columna por cada par que hayas encerrado en un círculo, colocar un 1 en la respuesta (si queda algún 1 suelto) y un 0 si no queda ningún 1 en la columna.
- Por ejemplo, si vas a sumar 1010 + 1111 + 1011 + 1110, deberás encerar en círculos 3 pares de 1 en el lugar de los ochos debido a que llévate un 1 dos veces desde la columna de los cuatros. Por consiguiente, deberás colocar un 0 en el lugar de los ochos a modo de respuesta y llevar tres 1 hacia la columna de los dieciséis. En esta columna, tienes un par de 1 y uno suelto, por lo que deberás colocar un 1 en la respuesta y otro en la columna de los treintaidós a modo de respuesta. Por lo tanto, 1010 + 1111 + 1011 + 1110 = 110010.
-
8Verifica tu respuesta. Existen varias calculadoras en línea que podrán ayudarte a sumar números binarios.[9]
Referencias
- ↑ http://www.math.grin.edu/~rebelsky/Courses/152/97F/Readings/student-binary
- ↑ http://csunplugged.org/binary-numbers/
- ↑ http://mtl.math.uiuc.edu/non-credit/compconn/bits/sample.html
- ↑ https://www.khanacademy.org/math/algebra-home/alg-intro-to-algebra/algebra-alternate-number-bases/v/number-systems-introduction
- ↑ http://www.math.grin.edu/~rebelsky/Courses/152/97F/Readings/student-binary
- ↑ https://www.mathsisfun.com/binary-digits.html
- ↑ http://www.math.grin.edu/~rebelsky/Courses/152/97F/Readings/student-binary
- ↑ https://courses.cs.vt.edu/csonline/NumberSystems/Lessons/AddingMultipleBinaryNumbers/index.html
- ↑ http://planetcalc.com/911/













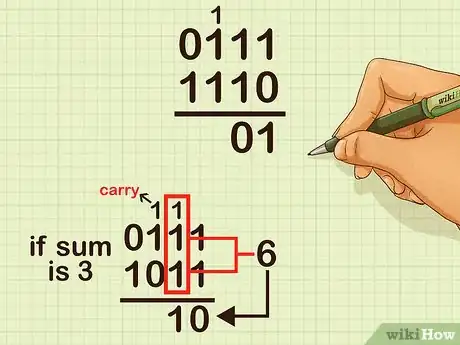





























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 91 676 veces.