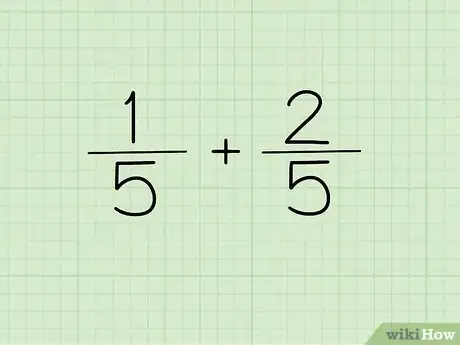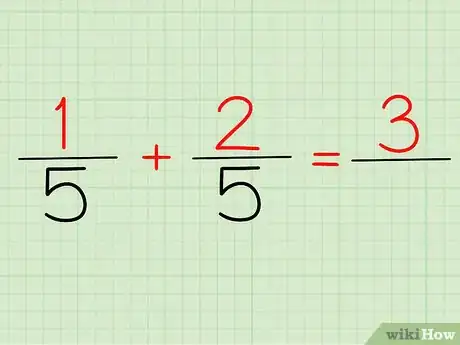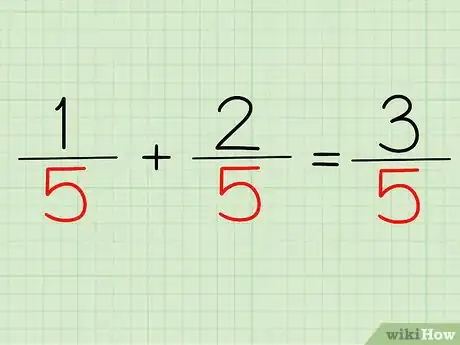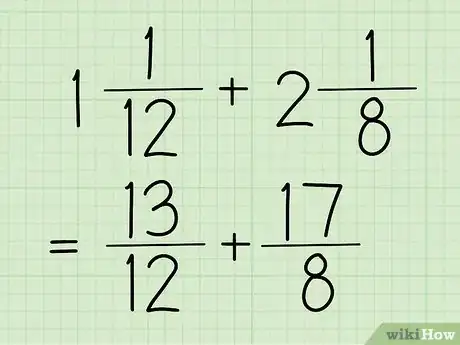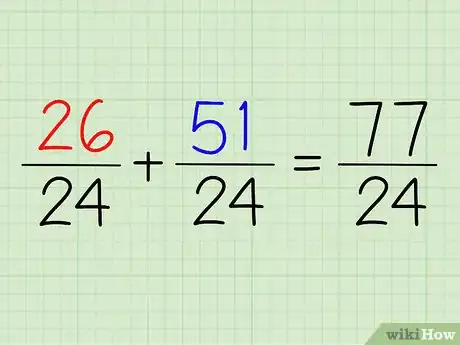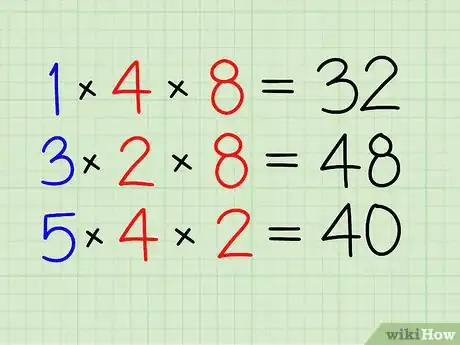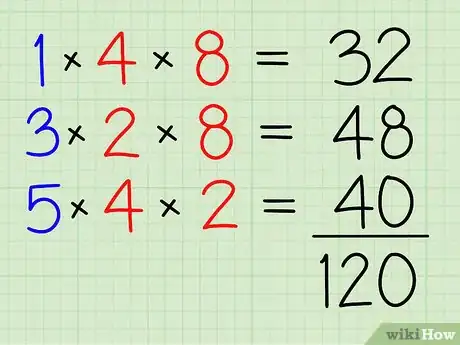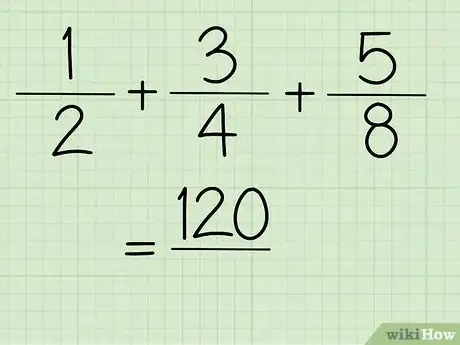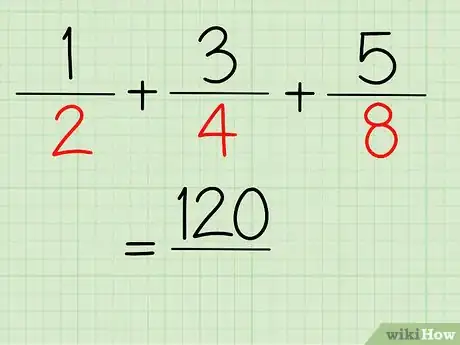wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 12 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 58 147 veces.
Sumar y restar fracciones es una habilidad esencial. Las fracciones son parte de la vida diaria, sobre todo en las clases de matemáticas, desde la escuela primaria hasta los estudios superiores. Sigue los pasos indicados a continuación para aprender a sumarlas y restarlas, ya sea que se trate de fracciones semejantes, no semejantes, mixtas o impropias. Una vez que entiendas el primer método, los demás serán bastante sencillos.
Pasos
Método 1
Método 1 de 4:Sumar y restar fracciones con el mismo denominador
-
1Escribe la ecuación. Si el denominador de las fracciones que debes sumar o restar es el mismo, colócalo también una sola vez como denominador en la respuesta.
- En otras palabras, 1/5 y 2/5 no tiene que escribirse como 1/5 + 2/5 = ?, sino que puede colocarse como (1+2)/5 = ?. Dado que el denominador es el mismo, puedes escribirlo solo una vez. Ambos numeradores van arriba.
-
2Suma los numeradores. El “numerador” es el número que se encuentra en la parte superior de una fracción. En el ejemplo, 1/5 y 2/5, los numeradores son 1 y 2.
- Ya sea que escribas la expresión como 1/5 + 2/5 o (1+2)/5, la respuesta deberá ser la misma: 3, ya que 1 + 2 = 3.
-
3No cambies el denominador. Dado que trabajarás con un denominador constante, no tienes que hacer nada con él. No lo sumes, restes, multipliques o dividas. Simplemente déjalo tal como está.
- En el ejemplo, el denominador es 5. Y eso es todo. Ese es el número que va en la parte inferior de la fracción final. Es la mitad de la respuesta.
-
4Halla la respuesta. Ahora, lo único que tienes que hacer es anotar el numerador y el denominador. En el ejemplo antes mencionado, la respuesta es 3/5.
- ¿Cuál era el numerador? 3. ¿Y el denominador? 5. Por lo tanto, 1/5 + 2/5, o (1 + 2)/5, es igual a 3/5.
Método 2
Método 2 de 4:Sumar y restar fracciones con denominadores distintos
-
1Halla el mínimo común denominador. Este es el menor número que tienen en común ambos denominadores. Toma como ejemplo las fracciones 2/3 y ¾. ¿Cuáles son los denominadores? 3 y 4. Puedes hallar el mínimo común denominador de ambos de tres formas.
- Escribe los múltiplos. Los múltiplos de 3 son 3, 6, 9, 12, 15, 18 y así sucesivamente. Los múltiplos de 4 son 4, 8, 12, 16, 20, etc. ¿Cuál es el menor número que se repite en ambas series? 12. Por lo tanto, este es el mínimo común denominador, o MCD.
-
Factoriza el número en sus componentes primos. Si sabes qué son los factores, puedes hacer la factorización prima. Esto es, hallar qué números pueden dar como resultado a los denominadores. Para el número 3, los factores son 3 y 1. Para el 4, los factores son 2 y 2. Multiplícalos todos: 3 x 2 x 2 = 12. La respuesta es el MCD.
- Si son números pequeños, multiplícalos entre sí. En algunos casos, como este ejemplo, puedes simplemente multiplicar los denominadores uno por el otro: 3 x 4 = 12. Sin embargo, si son números grandes, es mejor no hacerlo. No querrás multiplicar 56 x 44 y tener que trabajar con el número 2464 como parte de tu respuesta.
-
2Multiplica el denominador por el número que necesitas para hallar el MCD. En otras palabras, la idea es que los denominadores sean el mismo número; el MCD. En el ejemplo, el denominador debe ser 12. Para convertir 3 en 12, tienes que multiplicar 3 x 4. Para convertir 4 en 12, tienes que multiplicar 4 x 3. El número resultante será el denominador de la respuesta.
- Entonces, 2/3 se convierte en 2/3 x 4 y ¾ en ¾ x 3. Esto significa que las fracciones se transforman en 2/12 y 3/12. Pero aún no termina el proceso.
- Quizá notes que los denominadores, en este caso, se multiplican uno por el otro. Esta situación es particular en este caso, pero no se aplica para todos. A veces, en lugar de multiplicarlos entre sí, es necesario multiplicar cada uno por números distintos para hallar la respuesta.
- En otros casos, a veces solo tienes que multiplicar uno de los denominadores para igualarlo al denominador de la otra fracción de la ecuación.
- Entonces, 2/3 se convierte en 2/3 x 4 y ¾ en ¾ x 3. Esto significa que las fracciones se transforman en 2/12 y 3/12. Pero aún no termina el proceso.
-
3Multiplica el numerador por ese número también. Cuando multiplicas el denominador por un número, también tienes que multiplicar el numerador por el mismo número. Lo que se hizo en el paso anterior es solo la mitad de la multiplicación.
- El primer paso era 2/3 x 4 y 2/4 x 3. En el segundo paso se completan las expresiones de la siguiente manera: 2 x 4/3 x 4 y 3 x 3/ 4 x 3. Esto significa que las nuevas fracciones son 8/12 y 9/12.
-
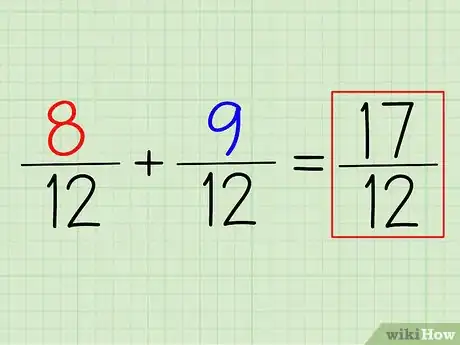
4Suma (o resta) los numeradores para hallar la respuesta. Para sumar 8/12 + 9/12, lo único que debes hacer es sumar los numeradores. Recuerda que ahora debes dejar el denominador tal cual está. El número que hallaste como MCD es el denominador final.
- Para este ejemplo, la resolución sería (8+9)/12 = 17/12. Para convertir la respuesta en una fracción mixta, simplemente resta el denominador del numerador para ver qué queda. En este caso, sería 17/12 = 1 5/12.
Método 3
Método 3 de 4:Sumar y restar fracciones mixtas e impropias
-
1Convierte una fracción mixta en una fracción impropia. Se llama fracciones mixtas a las fracciones compuestas por un número entero y una fracción, como en el ejemplo anterior (1 5/12). Por otro lado, una fracción impropia es aquella donde el numerador (el número de arriba) es mayor que el denominador (el número de abajo). Esto también se puede observar en el ejemplo anterior: 17/12.
- El ejemplo para esta sección será 13/12 y 17/8.
-
2Halla el denominador común. Recuerda que hay tres maneras de calcularlo: anotar los múltiplos, utilizar la factorización prima o multiplicar los denominadores entre sí.
- Primero, halla los múltiplos de los denominadores de este ejemplo, 12 y 8. ¿Cuál es el número menor que comparten? 24. Sus múltiplos son 8, 16 y 24, y 12 y 24. No tienes que ir muy lejos para hallarlo.
-
3Multiplica los numeradores y denominadores para conseguir fracciones semejantes. Ambos denominadores deben convertirse en 24. ¿Entonces cómo conviertes 12 en 24? Lo multiplicas por 2. ¿Y para convertir 8 en 24? Lo multiplicas por 3. No olvides que debes multiplicar los numeradores también.
- Por lo tanto, 13 x 2/12 x 2 = 26/24 y 17 x 3/8 x 3 = 51/24. Con esto, estarás en buen camino para resolver el problema.
-
4Suma o resta las fracciones. Una vez que tus fracciones tengan el mismo denominador, simplemente puedes sumar los numeradores. Recuerda que debes dejar el denominador tal cual está.
- Por ejemplo, 26/24 + 51/24 = 77/24. Ahí está la respuesta. Pero el numerador es bastante grande.
-
5Vuelve a convertir la respuesta en una fracción mixta. Tener un número tan grande como numerador es un poco extraño, ya que no te permite apreciar bien la magnitud de la fracción. Lo único que tienes que hacer es restar el denominador del numerador hasta que ya no se pueda y así ver qué número queda.
- Por ejemplo, puedes restar 24 de 77 tres veces. Si calculamos 24 x 3 =72; es decir, sobra 5. Por lo tanto, la respuesta final es 3 5/24. Y eso es todo.
Método 4
Método 4 de 4:Sumar y restar fracciones sin calcular el mínimo común denominador (MCD)
-
1Haz una lista de las fracciones.
- Por ejemplo, ½ + ¾ + ⅝.
-
2Primero halla el numerador.
- Multiplica 1 por los denominadores de las otras fracciones.
- Multiplica 1 por 4 y por 8. La respuesta es 32.
-
3Repite el proceso con los otros numeradores.
- Multiplica 3 por 2 y por 8. La respuesta es 48.
- Por último, multiplica 5 por 4 y por 2. La respuesta es 40.
-
4Suma todos los productos.
- Según el ejemplo, 32 + 48 + 40 = 120.
-
5De esta manera, habrás hallado el numerador final.
-
6Ahora, halla el denominador.
-
7Multiplica todos los denominadores.
- Según el ejemplo, 2 × 4 × 8 = 64.
-
8De esta manera obtendrás la respuesta final.
- Según el ejemplo, 120/64 = 1 56/64 = 1 ⅞.
Advertencias
- Tal vez tengas que multiplicar números grandes con estos métodos.
- Quizá necesites una calculadora.