Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 27 901 veces.
La regla empírica, a la que también se le conoce como la regla 68,5-95-99,7, constituye una manera útil de analizar datos estadísticos. Sin embargo, solo funciona para una distribución normal (la campana de Gauss) y solo es posible producir estimaciones. Será necesario que conozcas la media y la desviación estándar de los datos, pero, en caso de que vayas a emplear la regla empírica para una clase o un examen, se te deberá brindar esta información. Luego podrás usar esta regla para fines como estimar cuántos de los datos se encuentran dentro de un rango determinado.
Pasos
Parte 1
Parte 1 de 2:Disponer la curva
-
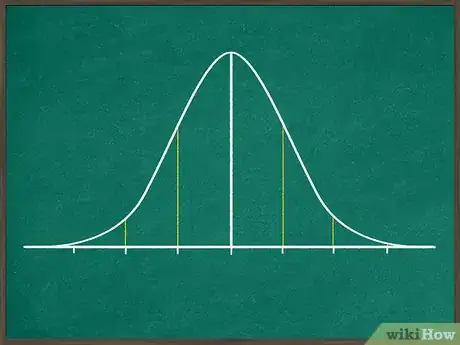
1Traza y divide una distribución normal. Haz un bosquejo de una curva normal cuyo punto más alto se encuentre en el centro y cuyos extremos se inclinen hacia abajo y vayan estrechándose de manera simétrica a la izquierda y la derecha. Luego traza varias líneas verticales que se intersequen con la curva de la siguiente manera:[1]
- Una línea debe dividir la curva por la mitad.
- Traza 3 líneas a la derecha de esta línea central y otras 3 a la izquierda. Estas líneas deben dividir cada una de las mitades de la curva en tres secciones espaciadas de manera uniforme y una sección pequeña en el extremo.
-
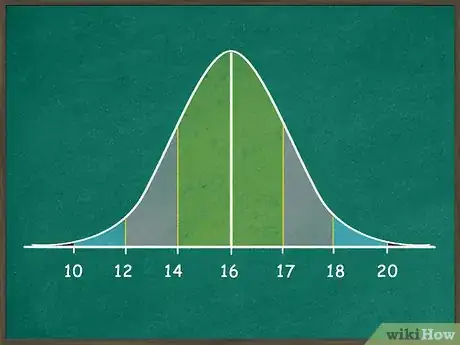
2Escribe los valores de la distribución normal en las líneas divisorias. Marca la línea que esté en el centro con la media de tus datos y luego suma las desviaciones estándar para obtener los valores correspondientes a las 3 líneas a la derecha. Resta las desviaciones estándar a la media y obtendrás los valores correspondientes a las 3 líneas a la izquierda. Por ejemplo:[2]
- Imagina que la media de los datos es 16 y la desviación estándar es 2. Marca la línea central con el número 16.
- Suma las desviaciones estándar para marcar la primera línea a la derecha del centro con el número 18, la siguiente de la derecha con el número 20 y la línea en el extremo derecho con el número 22.
- Resta las desviaciones estándar para marcar la primera línea a la izquierda del centro con el número 14, la siguiente de la izquierda con el número 12 y la línea en el extremo izquierdo con el número 10.
-
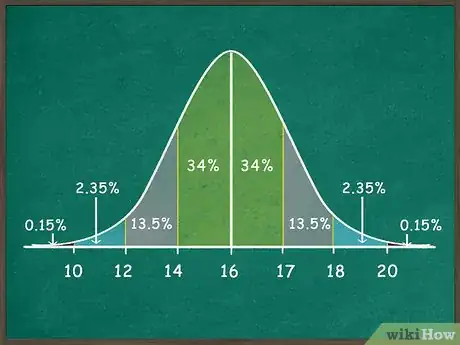
3Marca los porcentajes de cada sección. La regla empírica del punto base es fácil de comprender: el 68 % de los puntos de datos para una distribución normal se encontrarán dentro de una desviación estándar de la media, el 95 % dentro de dos desviaciones estándar y el 99,7 % dentro de tres desviaciones estándar. Puedes recordártelo marcando cada sección con un porcentaje de la siguiente forma:[3]
- Cada sección que se encuentre inmediatamente a la derecha y a la izquierda de la línea central contendrá el 34 %, sumando un total de 68.
- Las secciones siguientes a la derecha y la izquierda contendrán cada una el 13,5 %. Súmalas al 68 % y obtendrás el 95 % de los datos.
- Las secciones siguientes a cada lado contendrán cada una 2,35 % de los datos. Súmalos al 95 % y obtendrás el 99,7 % de los datos.
- Las puntas diminutas restantes de los datos a la izquierda y la derecha contienen cada una 0,15 % de los datos restantes, lo cual suma un total de 100 %.
Anuncio
Parte 2
Parte 2 de 2:Usar la curva para resolver problemas
-
1Encuentra las distribuciones de tus datos. Utiliza la media y la regla empírica para encontrar las distribuciones de los datos a 1, 2 y 3 desviaciones estándar de la media. Toma nota de ellos en la curva como referencia. Por ejemplo, imagina que vas a analizar el peso de una población de gatos, siendo la media del peso 4 kg y la desviación estándar 0,5 kg. Ten en cuenta lo siguiente:[4]
- 1 desviación estándar por encima de la media sería 4,5 kg y una desviación estándar por debajo de la media sería 3,5 kg.
- 2 desviaciones estándar por encima de la media sería 5 kg y 2 desviaciones estándar por debajo de la media sería 3 kg.
- 3 desviaciones estándar por encima de la media sería 5,5 kg y 3 desviaciones estándar por debajo de la media sería 2,5 kg.
-
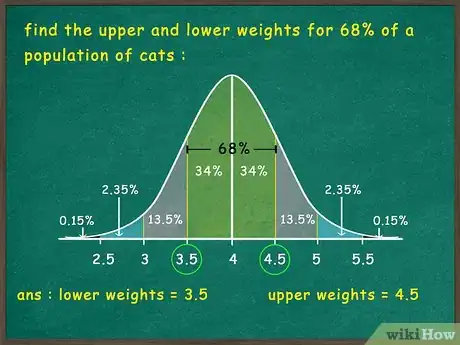
2Determina la sección de la curva que la pregunta te pida que analices. Cuando hayas dispuesto la curva, puedes resolver preguntas de análisis de datos mediante la regla empírica y la aritmética simple. Para empezar, lee con cuidado la pregunta para así determinar cuáles son las secciones con las que debas trabajar. Por ejemplo:[5]
- Imagina que se te pide que encuentres el peso superior y el inferior para el 68 % de una población de gatos. Será necesario que trabajes con las dos secciones más cercanas al centro, en donde se encontrará el 68 % de los datos.
- De forma similar, imagina que la media del peso es 4 kg y la desviación estándar es 0,5 kg. En caso de que se te pida encontrar la proporción de gatos cuyo peso supere los 5 kg, deberás trabajar con la sección en el extremo derecho (a 2 desviaciones estándar de la media).
-
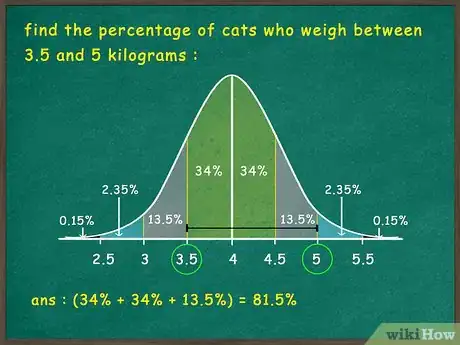
3Encuentra el porcentaje de los datos que estén dentro de un rango determinado. En caso de que se te pida encontrar el porcentaje de la población dentro de un rango determinado, lo único que debes hacer es sumar los porcentajes dentro de un conjunto dado de desviaciones estándar. Por ejemplo, si lo que se te pide es encontrar el porcentaje de gatos cuyo peso sea de entre 3,5 y 5 kg, siendo la media de 4 kg y la desviación estándar de 0,5 kg, deberás tener en cuenta lo siguiente:[6]
- 2 desviaciones estándar por encima de la media equivaldrán a 5 kg, mientras que 1 desviación estándar por debajo de la media equivaldrá a 3,5 kg.
- Esto quiere decir el 81,5 % (68 % + 13,5 %) de los gatos pesa entre 3,5 y 5 kg.
-
4Encuentra puntos y rangos de datos empleando los porcentajes de las secciones. Utiliza la información que te brinden las distribuciones de porcentajes y las desviaciones estándar para encontrar los límites superiores e inferiores para secciones de tus datos. Por ejemplo, una pregunta acerca de tus datos sobre el peso de los gatos podría ser “¿Cuál es el límite superior de peso del 2,5 % más bajo de los gatos?”.[7]
- El 2,5 % más bajo de los datos se encontraría 2 desviaciones estándar por debajo de la media.
- Si es que la media es 4 kg y la desviación estándar es 0,5 kg, el peso del 2,5 % más bajo de los gatos será 3 kg o menos (4 - 0,5 x 2).
Anuncio
Referencias
- ↑ http://www.stat119review.com/more-material/normal-distribution/empirical-rule/solving-empirical-rule-questions
- ↑ https://www.khanacademy.org/math/probability/normal-distributions-a2/normal-distributions-a2ii/v/ck12-org-normal-distribution-problems-empirical-rule
- ↑ http://www.stat119review.com/more-material/normal-distribution/empirical-rule/solving-empirical-rule-questions
- ↑ https://www.youtube.com/watch?v=T7-eeg6rhjY
- ↑ http://www.stat119review.com/more-material/normal-distribution/empirical-rule/solving-empirical-rule-questions
- ↑ https://www.khanacademy.org/math/probability/normal-distributions-a2/normal-distributions-a2ii/v/ck12-org-normal-distribution-problems-empirical-rule
- ↑ https://www.nku.edu/~statistics/212_Using_the_Empirical_Rule.htm

























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 27 901 veces.