Comment calculer la moyenne l’écart type et l’erreur type

Informations concernant l'auteur.e

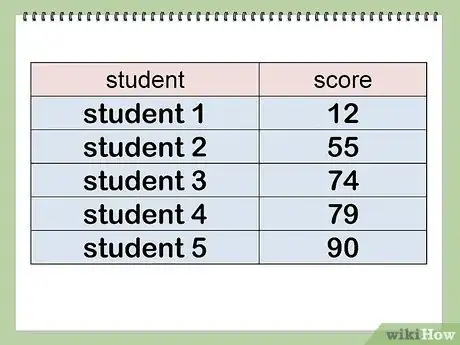
La collecte de données statistiques a souvent pour but d'analyser une situation afin d'en tirer des conclusions. Cette analyse repose en premier sur la détermination de certains indicateurs bien ciblée, ce peut, par exemple, être la moyenne, l'écart type et l'erreur type de ces données, il en existe d'autres.

Méthode 1

Méthode 1 sur 4:
Comprendre des données statistiques

1
Choisissez une série de valeurs à analyser. Si vous travaillez sur une population entière, vous obtenez une série (c'est le cas que nous prendrons), et si c'est seulement sur une partie de la population, c'est un échantillon. Le nombre de valeurs considérées est l'effectif.
- Par exemple, un test a été donné à 5 étudiants. Les notes obtenues sur 100 sont les suivantes : 12, 55, 74, 79 et 90.
Publicité

Méthode 2

Méthode 2 sur 4:
Calculer une moyenne

1
Calculez la moyenne arithmétique. Additionnez toutes les valeurs de la série, puis divisez cette somme par le nombre de valeurs (effectif) de la série.
- Mathématiquement, la moyenne ${\bar {x}}$ (parfois aussi $\mu$ ) s'écrit ainsi : ${\bar {x}}={\frac {\sum \limits _{i=1}^{n}x_{i}}{n}}$ , $\sum$ est le symbole de la sommation, $x_{i}$ chacune des valeurs de l'échantillon et $n$ l'effectif de l'échantillon.
- Dans le cas du test, ${\bar {x}}={\frac {12+55+74+79+90}{5}}={\frac {310}{5}}=62$ .

Méthode 3

Méthode 3 sur 4:
Calculer un écart type

1
Calculez l'écart type ( $\sigma$ ). Il représente une mesure de dispersion des données par rapport à la moyenne. La formule de calcul est la suivante :
$\sigma ={\sqrt {\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})}{n}}}$ $\sigma ={\sqrt {\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})}{n}}}$ .
- Dans notre exemple, l'écart type est : $\sigma ={\sqrt {\frac {(12-62)^{2}+(55-62)^{2}+(74-62)^{2}+(79-62)^{2}+(90-62)^{2})}{5}}}$
  $\sigma ={\sqrt {\frac {(-50)^{2}+(-7)^{2}+(12)^{2}+(17)^{2}+(28)^{2})}{5}}}=27,4$ .
  (Nota bene : si vous savez que vos données sont celles d'un échantillon représentatif, dont vous ne connaissez pas la moyenne, divisez par n - 1 : c'est ce qu'on appelle un écart type sans biais ( $s$ ).
Publicité

Méthode 4

Méthode 4 sur 4:
Calculer une erreur type de la moyenne

1
Calculez l'erreur type (de la moyenne). Elle représente le degré de fiabilité de la moyenne de l'échantillon par rapport à la moyenne de l'ensemble d'une population. Plus l'échantillon est grand, plus l'erreur type est faible et plus la moyenne de l'échantillon se rapproche de la moyenne de la population d'origine. Divisez l'écart type par la racine carrée de $n$ $n$ , l'effectif de l'échantillon : $\sigma _{\bar {x}}={\frac {\sigma }{\sqrt {n}}}$ $\sigma _{\bar {x}}={\frac {\sigma }{\sqrt {n}}}$ .
- Ainsi, pour l'exemple ci-dessus, s'il s'agissait d'un échantillon de 5 étudiants sur une classe de 50. Les 50 étudiants avaient un écart type de 17 ( $\sigma =21$ ), l'erreur type est : $\sigma _{\bar {x}}={\frac {17}{\sqrt {5}}}=7,6$ .

Conseils

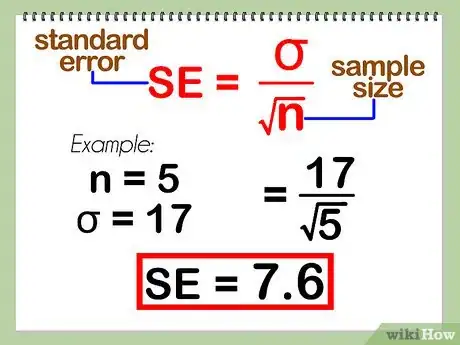
Les calculs de la moyenne, de l'écart type et de l’erreur type sont très utiles pour l'analyse de données normalement dispersées. L’intervalle de confiance à un écart type regroupe 68 % des données, celui à 2 écarts types regroupe 95 % des données et celui à 3 écarts types regroupe 99,7 % des données. L'erreur type devient de plus en plus petite au fur et à mesure de l’augmentation de la taille de l'échantillon
Calculis.net : un calculateur d'écarts types en ligne.