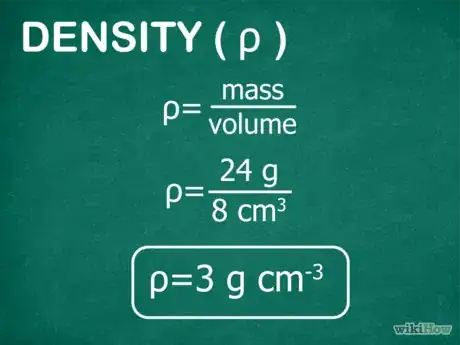Comment calculer le volume et la densité

Le volume est défini comme étant l'espace occupé par un objet, tandis que la densité est le rapport entre la masse de l'objet et le volume occupé par celui-ci ^{[1]
X
Source de recherche}. Pour connaitre la densité d'un objet donné, il est nécessaire de calculer son volume. Trouver le volume d'un solide régulier est plutôt simple, étant donné que vous pouvez simplement utiliser la formule pour le type d'objet en question. L'unité de volume du système international est le mètre cube (m³) et ses dérivés (dm³, cm³, mm³). Il existe cependant d'autres unités de volume, utilisées dans les pays anglo-saxons (le pouce cube, le pied cube). Une fois que vous connaissez le volume de votre objet, il vous sera plus facile de calculer la densité. Les unités de mesure couramment utilisées pour exprimer la densité sont les suivants : le gramme par centimètre cube (g/cm³) et le gramme par millilitre (g/ml).

Partie 1

Partie 1 sur 3:
Calculer le volume de plusieurs solides réguliers

1
Déterminez la forme de l'objet que vous étudiez. Connaitre la forme géométrique de l'objet que vous étudiez vous permet d'utiliser la formule appropriée et d'effectuer les mesures nécessaires pour calculer le volume.
- Une sphère : il s'agit d'un objet dans l'espace (en trois dimensions) parfaitement rond, dans lequel chaque point de la surface est à égale distance du centre. En d'autres termes, une sphère est un solide en forme de ballon ^{[2]
  X
  Source de recherche}.
- Un cône : il s'agit d'un solide en trois dimensions avec une base circulaire et un sommet unique (représenté par la pointe du cône). Autrement dit, c'est comme une pyramide dont la base est circulaire ^{[3]
  X
  Source de recherche}.
- Un cube : c'est une figure géométrique tridimensionnelle ayant six faces carrées identiques les unes aux autres ^{[4]
  X
  Source de recherche}.
- Un parallélépipède rectangle : cette figure est encore appelée un prisme rectangulaire. Elle ressemble à un cube en ce sens qu'elle a une forme en trois dimensions, sauf qu'ici les côtés sont rectangulaires et non carrés ^{[5]
  X
  Source de recherche}.
- Un cylindre : c'est un solide dans l'espace composé de deux faces planes de forme circulaire identiques reliées par un seul côté incurvé ^{[6]
  X
  Source de recherche}.
- Une pyramide : il s'agit d'un solide dans l'espace ayant un polygone comme base et des faces latérales qui convergent vers un seul sommet (la pointe de la pyramide ^{[7]
  X
  Source de recherche}). Une pyramide régulière est une pyramide ayant comme base un polygone régulier, qui n'est rien d'autre qu'une figure géométrique dont les côtés sont de même longueur et dont les angles sont égaux ^{[8]
  X
  Source de recherche}.
- Si la figure géométrique que vous étudiez a une forme irrégulière, vous pouvez déterminer son volume par la méthode du déplacement.
2
Choisissez correctement l'équation de votre solide. Chaque figure géométrique a sa propre formule pour calculer le volume. Voici les formules permettant de calculer les volumes de quelques solides. Consultez cet article pour plus d'informations à ce sujet.
- Pour une sphère : $V={\frac {4}{3}}\pi r^{3},$ où r est le rayon.
- Pour un cône : $V={\frac {1}{3}}\pi r^{2}h,$ où r est le rayon de la base circulaire, h la hauteur du cône.
- Pour un cube : $V=s^{3},$ où s est la longueur de n'importe quel côté.
- Pour un parallélépipède rectangle : $V=lwh,$ où l est la longueur d'un côté d'une face rectangulaire, w est la largeur d'une face rectangulaire et h la hauteur du prisme.
- Pour un cylindre : $\pi r^{2}h,$ où r est le rayon de la base circulaire et h la hauteur du cône.
- Pour une pyramide : $V={\frac {1}{3}}Bh,$ où B représente l'aire de la base de la pyramide et h la hauteur de la pyramide.
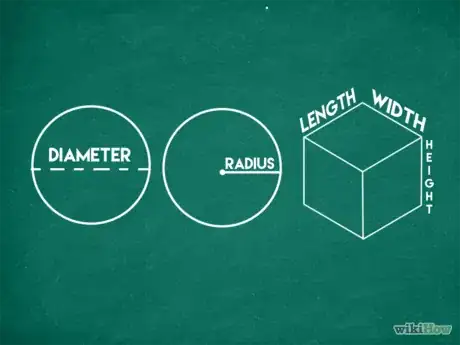
3
Effectuez les mesures nécessaires. Les mesures dont vous avez besoin pour vos calculs dépendent du type de solide que vous étudiez. Pour la plupart des figures géométriques, vous devez connaitre la hauteur. Vous aurez besoin de la longueur et de la largeur pour les figures à faces rectangulaires et si le solide que vous étudiez est de forme circulaire vous aurez besoin du rayon.
- Dans un cercle, le rayon est égal à la moitié du diamètre. Pour mesurer le diamètre, placez une règle le long du centre de la figure afin de lire la seconde extrémité de la règle. Maintenant, vous pouvez obtenir le rayon en divisant le diamètre par deux.
- Déterminez le rayon d'une sphère est légèrement plus complexe. Lisez cet article pour découvrir différentes façons de calculer le rayon d'un solide sphérique.
- Les grandeurs comme la longueur, la largeur et la hauteur d'un objet peuvent être simplement mesurées avec une règle. Il vous suffit de poser le zéro de la règle sur une des extrémités de l'objet et de lire l'autre bout de votre règle.
4
Calculez le volume. Après avoir déterminé la forme de l'objet, identifié la bonne formule à utiliser et effectué toutes les mesures possibles, vous pouvez maintenant calculer le volume. Entrez dans la formule les données dont vous disposez, puis effectuez les calculs nécessaires. Le résultat final représente le volume du solide en question.
- Souvenez-vous que le volume doit être exprimé en unités cubiques. Quel que soit le système de mesure que vous adoptez, le volume doit être cubique. À la fin de vos calculs, assurez-vous d'ajouter les unités de mesure appropriées pour exprimer le résultat obtenu.
Publicité

Partie 2

Partie 2 sur 3:
Calculer le volume d'un solide irrégulier

1
Calculez le volume d'un objet à l'aide de son déplacement. Mesurer les dimensions des objets de forme irrégulière peut être très complexe, ce qui peut conduire à des valeurs inexactes et des résultats erronés. Cela dit, en mesurant la quantité d'eau déplacée par un objet, vous pouvez facilement déterminer votre volume sans avoir recours à des formules complexes ^{[9]
X
Source de recherche}.
- Cette méthode peut également être utilisée pour calculer le volume d'un solide régulier.
2
Remplissez une éprouvette graduée avec de l'eau. Cet instrument de mesure est disponible dans tous les laboratoires. Il s'agit d'un récipient cylindrique ayant une échelle graduée à l'extérieur, permettant de mesurer le volume des liquides. Assurez-vous que votre éprouvette graduée est suffisamment grande pour contenir l'objet que vous étudiez. Maintenant, remplissez l'éprouvette avec de l'eau, de sorte que l'objet soit complètement submergé sans provoquer un débordement. Lisez et inscrivez quelque part le niveau initial de l'eau à l'intérieur du récipient.
- Au moment de lire cette mesure, assurez-vous de regarder l'eau au niveau des yeux et de lire la valeur au bas du ménisque. Le ménisque est la partie courbe de la surface d'un liquide qui se forme lorsque le liquide en question entre en contact avec une autre surface ^{[10]
  X
  Source de recherche}.
3
Mettez délicatement l'objet à l'intérieur du bécher. Veillez à ne pas le laisser tomber dans l'eau étant donné que cela pourrait entrainer des éclaboussures. En outre, vérifiez que l'objet est complètement immergé. Maintenant, lisez le nouveau niveau atteint par le liquide, une fois encore à hauteur des yeux tout en accordant une attention particulière au ménisque.
- Si une partie de l'eau déborde le bécher, essayez l'expérience à nouveau avec une grande éprouvette ou utilisez moins d'eau.
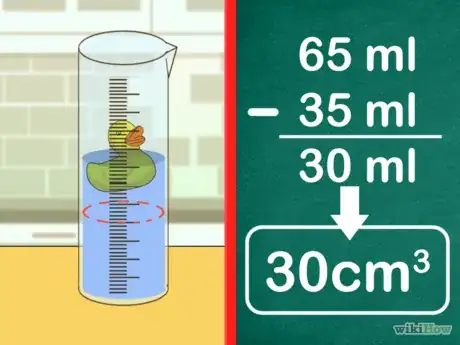
4
Soustrayez le nouveau niveau de l'eau de sa valeur initiale. La quantité d'eau déplacée par l'objet est égale au volume de ce dernier mesuré en centimètres cubes. Les liquides sont habituellement exprimés en millilitre, ce qui équivaut à un centimètre cube ^{[11]
X
Source de recherche}.
- Par exemple, si le niveau initial était de 35 ml et le niveau final est de 65 ml, cela signifie que le volume de l'objet étudié est égal à 65 - 35 = 30 ml ou 30 cm³
Publicité

Partie 3

Partie 3 sur 3:
Calculer la densité

1
Déterminez la masse d'un objet. La quantité de matière présente dans un objet détermine la masse de ce solide ^{[12]
X
Source de recherche}. La masse peut être mesurée directement, en pesant l'objet sur une balance et elle s'exprime en grammes.
- Trouvez une balance électronique précise, puis posez l'objet à peser. Notez la masse obtenue dans un carnet.
- Vous pouvez également utiliser une balance traditionnelle. Dans ce cas, vous aurez à placer l'objet sur un des plateaux de la balance et poser différents poids sur la seconde de sorte que les deux plateaux soient en parfait équilibre. La masse de l'objet en question sera égale à la masse totale des poids sur la balance.
- Il est très important de veiller à ce que l'objet dont vous mesurez la masse soit complètement sec. Cela permet de vous assurer que la quantité d'eau absorbée ne peut pas fausser la précision de la mesure du poids.
2
Calculez le volume de votre objet. Si l'objet en question est de forme régulière, vous pouvez calculer le volume en utilisant l'une des formules présentées dans les méthodes énumérées ci-dessus. S'il est par contre de forme irrégulière, vous devez utiliser la méthode de déplacement décrite précédemment.
3
Calculez la densité. La densité d'un objet est définie comme étant la masse du solide divisée par son volume. Pour calculer cette grandeur, divisez la valeur de la masse mesurée par le volume calculé. Le résultat obtenu est exprimé en g/cm³.
- Par exemple, calculons la densité $\rho$ d'une substance ayant un volume égal à 8 cm³ et une masse de 24 g.
- ${\begin{aligned}\rho &={\frac {M}{V}}\\&={\frac {24{\rm {\ g}}}{8{\rm {\ cm^{3}}}}}\\&=3{\rm {\ g\ cm^{-3}}}\end{aligned}}$
Publicité

Conseils

Les objets que vous rencontrerez dans les problèmes mathématiques seront souvent des combinaisons simples formées par d'autres solides géométriques connus. Vous devrez reconnaitre chacun d'eux et calculer le volume pour chaque figure, puis additionner tous les résultats partiels pour obtenir le volume total.
Vous pouvez vérifier vos calculs en utilisant la méthode de déplacement et en comparant vos résultats.