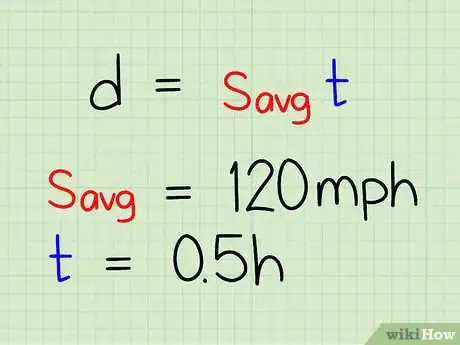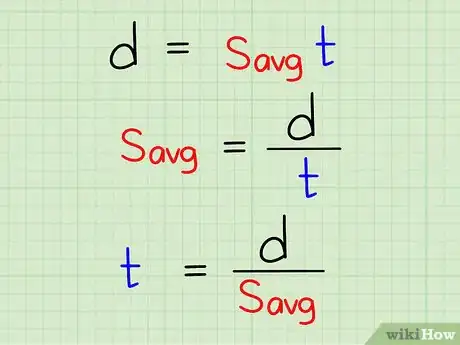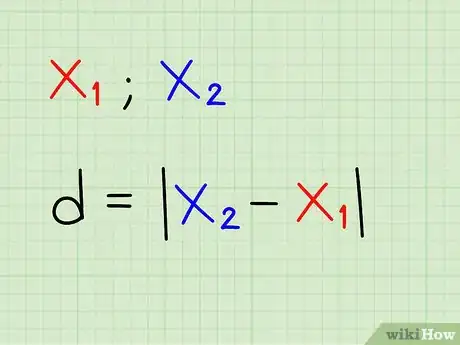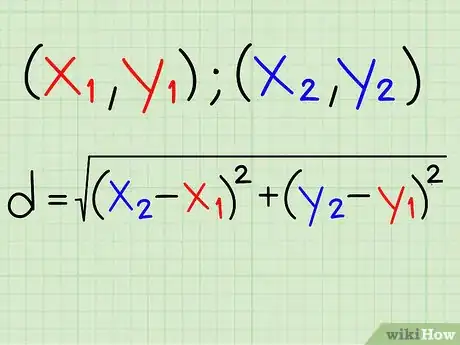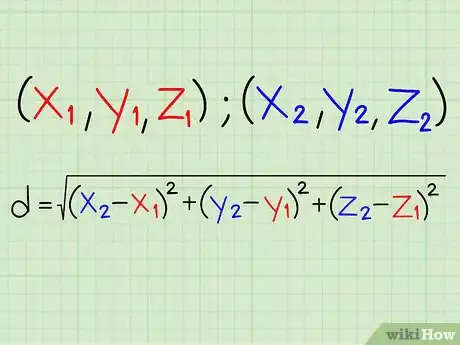wikiHow est un wiki, ce qui veut dire que de nombreux articles sont rédigés par plusieurs auteurs(es). Pour créer cet article, 10 personnes, certaines anonymes, ont participé à son édition et à son amélioration au fil du temps.
Cet article a été consulté 176 099 fois.
La distance, que l'on désigne le plus souvent par la lettre d, est la mesure entre deux points en ligne droite. Cette distance peut être calculée entre deux points fixes (par exemple, la distance chez une personne, qui va du haut de sa tête à sa plante des pieds, c'est la taille) ou entre un point fixe et un objet en déplacement. Dans ce dernier cas, on ne peut calculer la distance qu'à un temps T précis. La distance se calcule le plus souvent à l'aide de la formule suivante : d = v × t dans laquelle « d » est la distance, « v », la vitesse et « t » le temps de parcours. La distance peut aussi se calculer entre deux points d'un plan grâce à la formule : d = √((x2 - x1)2 + (y2 - y1)2, dans laquelle (x1, y1) et (x2, y2) sont les coordonnées de vos deux points. Entrons dans le détail de ces deux cas de figure.
Étapes
Méthode 1
Méthode 1 sur 2:Calculer une distance en connaissant la vitesse et le temps de parcours
-
1Il vous faut deux valeurs, la vitesse et le temps de parcours. Deux informations sont essentielles si vous voulez pouvoir calculer la distance (d) parcourue par un objet en mouvement : sa vitesse (v) et le temps de parcours (t). Alors, vous pourrez utiliser la formule suivante : d = v × t.
- Afin de mieux comprendre, prenons un exemple. Admettons que vous rouliez à une vitesse de 120 km/h et que vous vouliez savoir quelle distance sera parcourue en 30 minutes à cette vitesse. Votre vitesse est donc de 120 km/h et votre temps de parcours est de 0,5 heure. C'est l'exemple qui nous servira tout au long de cette partie.
-
2Multipliez la vitesse par le temps. Le calcul de la distance est d'une simplicité enfantine, puisqu'il suffit simplement de multiplier les deux données.
- Il faut cependant faire très attention aux unités de ces deux valeurs. Elles doivent être cohérentes. Ainsi, si la vitesse est en km/h et que le temps est en minutes, il faut transformer ces dernières en heures. Pour ce faire, divisez vos minutes par 60.
- Reprenons notre problème : 120 km/h x 0,5 heure = 60 kilomètres. Vous aurez remarqué que les deux données sont spécifiées en heures. Pourtant, les heures disparaissent de la réponse. C'est par ce qu'on a simplifié les unités. Des heures sont en dénominateur (vitesse) et des heures sont en numérateur (temps). On les annule purement et simplement, il ne reste plus que des kilomètres.
-
3Il est possible de manipuler la formule pour calculer une des autres variables. La formule de calcul est très simple et donc facile à modifier. Il suffit d'isoler la variable qui vous intéresse, la vitesse ou le temps, en respectant certaines règles d'algèbre. La formule dérivée pour le calcul de la vitesse en fonction de la distance et du temps est : v = d/t. La formule dérivée pour le calcul du temps en fonction de la distance et de la vitesse est : t = d/v.
- Admettons qu'une voiture ait couvert une distance de 60 kilomètres en 50 minutes, mais vous vous demandez qu'elle a bien pu être sa vitesse moyenne. On a la distance, le temps, on applique la formule : v = d/t. Il faut diviser la distance par le temps, soit 60 kilomètres / 50 minutes. La vitesse est de 1,2 km/min.
- Vous noterez que l'unité de la réponse n'est pas habituelle, des km/min ! On compte plutôt en km/h. Pour faire la conversion, il suffit de multiplier la réponse par 60, ce qui donne : 72 km/h.
-
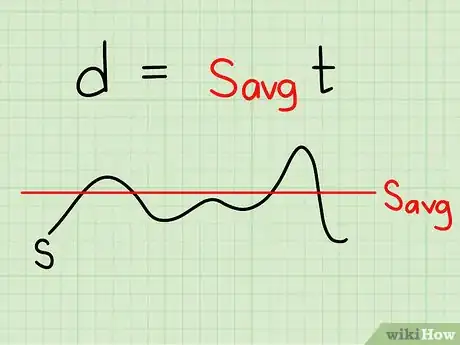
4Cela n'a pas été précisé avant, mais on suppose toujours que la vitesse « v » de l'objet en déplacement est constante. C'est pourquoi on parle de vitesse moyenne. Si l'objet en mouvement a des vitesses variables, on prend toujours la vitesse moyenne pour simplifier les calculs. C'est ce qu'on rencontre le plus souvent dans les exercices de mathématiques ou de physique. Dans la réalité, rares sont les objets à se déplacer à vitesse constante, ils peuvent ralentir, accélérer, s'arrêter…
- Dans notre exemple, nous avons trouvé qu'on roulait à une vitesse moyenne de 72 km/h, puisqu'il avait fait 60 kilomètres en 50 minutes. Admettons maintenant que nous ayons roulé à 80 km/h sur la moitié du parcours, puis à 64 km/h sur l'autre moitié. Vous avez également parcouru 60 kilomètres en 50 minutes — le premier tronçon a été parcouru en 22,5 minutes ((60 x 30) / 80) et le second, en 27,5 minutes ((60 x 30)/64).
- À un stade plus avancé en mathématiques, on doit utiliser, pour des objets ayant des vitesses variables, les dérivées. C'est nettement plus compliqué !
Publicité
Méthode 2
Méthode 2 sur 2:Calculer une distance en connaissant deux points (dans un espace mathématique)
-
1Trouvez deux points avec leurs coordonnées («x », « y » et éventuellement « z »). On a vu comment on calculait une distance avec un objet qui se déplaçait. On peut aussi calculer la distance entre deux objets ou deux points fixes. Vous le comprenez, ce qu'on a vu précédemment ne nous est d'aucune utilité, puisque les repères sont fixes. N'empêche qu'il y a bien une distance entre eux ! Il existe une formule qui permet de calculer la distance entre deux points fixes, il suffit de connaitre les coordonnées (à une, deux ou trois dimensions) de ces points. Si ces derniers sont dans un espace à une seule dimension (une droite), vous n'avez besoin que de deux coordonnées, les abscisses x1 et x2, par exemple. Dans un espace à deux dimensions (un plan), vous aurez besoin des coordonnées complètes des deux points (x1, y1) et (x2, y2). Enfin, dans un espace à trois dimensions, vous aurez besoin des coordonnées complètes des deux points (x1, y1, z1) et (x2, y2, z2).
-
2Dans un espace à une seule dimension, il suffit de faire la soustraction des deux points. C'est très simple, mais il y a juste une petite difficulté, la soustraction peut être négative, donc il faut prendre la valeur absolue du résultat : ce sera la distance entre les deux points. La formule littérale est donc la suivante : d =|x2 - x1|. Concrètement, avec cette formule, on fait la soustraction entre x1 et x2, puis on prend la valeur absolue.
- Notez au passage comment on figure la valeur absolue : c'est le symbole « || ». Prendre la valeur absolue d'une valeur, positive ou négative, consiste à enlever son signe, si bien que la valeur est toujours positive.
- Imaginez que vous vous soyez arrêté au bord de la route et que la prochaine ville devant vous soit à 5 km et la dernière ville que vous avez traversée soit à 1 km derrière vous. Question : quelle est la distance entre ces deux villes ? Posons que la première ville a comme coordonnées x1 = 5 et la seconde, x2 = -1. À l'aide de la formule, rien de plus simple que de trouver la distance. Voici comment il faut procéder :
- d =|x2 - x1|
- =|-1 - 5|
- =|-6|= 6 kilomètres
-
3Dans un espace à deux dimensions, la distance se calcule en passant par le célèbre (mais redoutable) théorème de Pythagore. C'est un peu plus compliqué qu'avec une seule dimension, mais c'est faisable. La formule de la distance est alors la suivante : d = √((x2 - x1)2 + (y2 - y1)2). En clair, on soustrait les abscisses («x ») et l'on élève au carré. On fait de même avec les ordonnées («y »). On additionne ensuite les deux résultats et l'on prend la racine carrée. Vous avez votre distance ! Cela ne marche que dans un plan cartésien (orthonormé par exemple) avec les deux axes « x » et « y ».
- En deux dimensions, on utilise donc le théorème de Pythagore, qui stipule que l'hypoténuse d'un triangle rectangle est égale à la racine carrée de la somme des carrés des deux autres cotés. L'hypoténuse est le côté le plus long d'un triangle rectangle et représente en fait la distance entre nos deux points.
- Soit deux points dans un plan cartésien de coordonnées respectives : (3, -10) et (11, 7), le premier est le centre d'un cercle, tandis que le second est un point du cercle. Pour trouver la distance entre les deux, c'est-à-dire le rayon, on procède comme suit :
- d = √((x2 - x1)2 + (y2 - y1)2)
- d = √((11 - 3)2 + (7 -(-10))2) = √((8)2 + (17)2)
- d = √(64 + 289)
- d = √(353) = 18,79
-
4Dans un espace à trois dimensions, il faut modifier légèrement la formule précédente. Dans ce genre d'espace, les points ont une troisième dimension « z », en plus de « x » et « y ». La formule de la distance est alors la suivante : d = √((x2 - x1)2 + (y2 - y1)2 + (z2 - z1)2). Vous le voyez la formule est quasiment la même, on a juste rajouté la dimension « z ». Comme pour « x » et « y" », on fait la différence des deux coordonnées « z », on élève au carré le résultat et ajoute aux autres carrés. Au final, on prend la racine carrée de la somme des « x », des « y » et des « z ».
- Imaginons que vous soyez un astronaute sorti dans l'espace et que vous soyez à proximité deux astéroïdes. Le premier d'entre eux est à 8 km devant, à 2 km sur votre droite et à 5 kilomètres en dessous. Le second est à 3 km derrière vous, à 3 km sur votre gauche et à 4 km au-dessus de vous. On est bien dans un espace à trois dimensions et vos astéroïdes ont alors comme coordonnées respectives : (8, 2, -5) et (-3, -3, 4). Le calcul de la distance entre les deux corps célestes s'opère de la façon suivante :
- d = √((-3 - 8)2 + (-3 - 2)2 + (4 - -5)2)
- d = √((-11)2 + (-5)2 + (9)2)
- d = √(121 + 25 + 81)
- d = √(227) = 15,07 km
Publicité