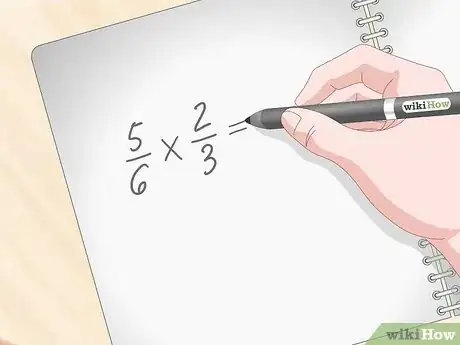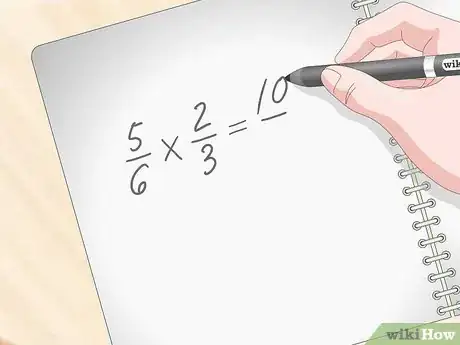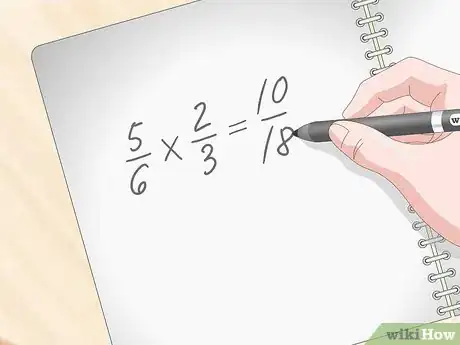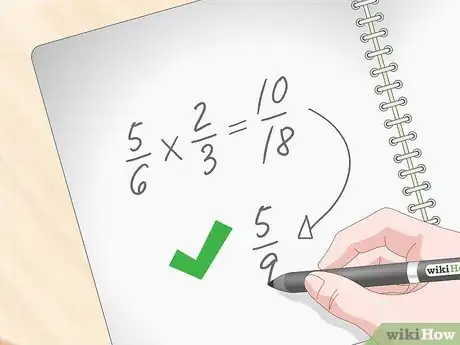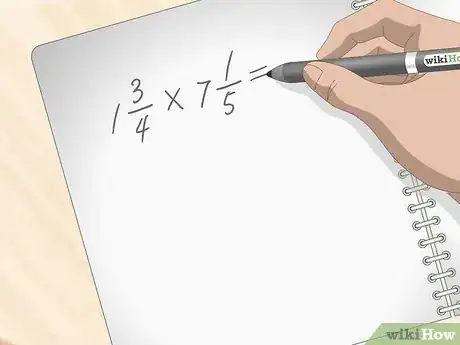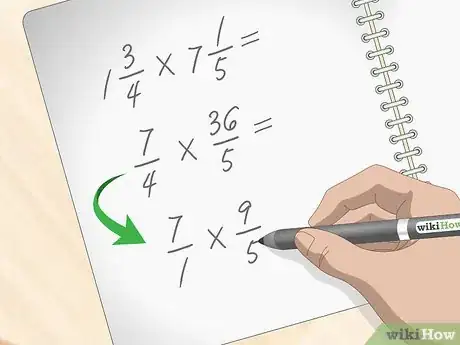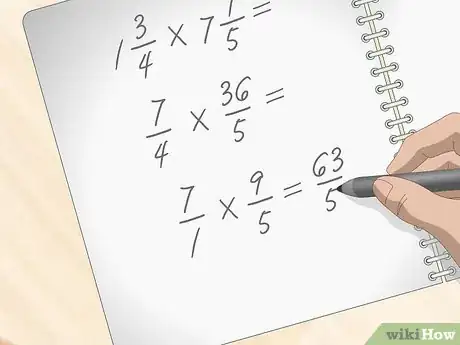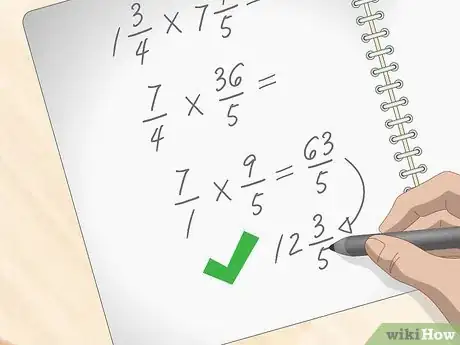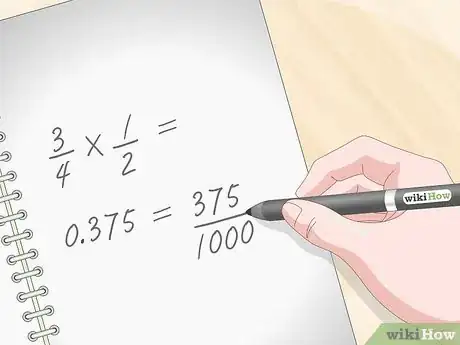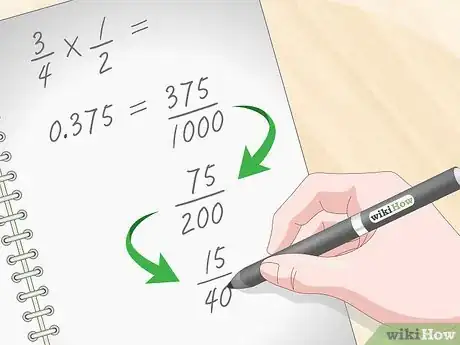Comment multiplier des fractions

Multiplier des fractions et des nombres fractionnaires peut sembler complexe à quelqu'un d'inexpérimenté, mais en fait c'est beaucoup plus simple que de les additionner. Les nombres fractionnaires doivent être transformés dans un premier temps en fractions impropres, il faut ensuite multiplier les numérateurs, puis les dénominateurs. Pour terminer, si cela est possible, il faut simplifier le résultat qui est une fraction. Ce n'est donc pas compliqué, il faut juste être attentif lors de ces différentes étapes.

Méthode 1

Méthode 1 sur 3:
Multiplier des fractions simples

1
Inscrivez l'opération sur une feuille de papier. Écrire les différentes étapes de cette multiplication vous aidera à mieux comprendre. C'est aussi intéressant, car en cas d'erreur, vous allez pouvoir l'identifier rapidement. Toute fraction est composée d'un numérateur (nombre du haut) et d'un dénominateur (nombre du bas). Entre les deux, il y a un trait horizontal, dit « trait de fraction ».
- Écrivez toujours vos fractions en alignant sur une même horizontale les traits de fraction. Vous éviterez ainsi bien des erreurs !
CONSEIL D'EXPERT(E)

Simplifiez la fraction le plus possible avant de faire la multiplication, ainsi les nombres sont plus courts.

Grace Imson, MA
Professeure de mathématiques au City College of San Francisco
Grace Imson est une professeure de mathématiques ayant plus de 40 ans d'expérience dans l’enseignement. Grace exerce actuellement au City College de San Francisco. Auparavant, elle était professeure au département de mathématiques de l'université Saint-Louis. Elle a enseigné cette discipline aux niveaux primaire, intermédiaire, secondaire et universitaire. Elle est titulaire d'un master en éducation avec une spécialisation en administration et supervision, délivré par l'université Saint-Louis.

Grace Imson, MA
Professeure de mathématiques au City College of San Francisco
2
Multipliez dans un premier temps les numérateurs. Ainsi, si vous devez trouver le résultat de ${\frac {5}{6}}\times {\frac {2}{3}}$ ${\frac {5}{6}}\times {\frac {2}{3}}$ , faites dans un premier temps $5\times 2$ $5\times 2$ , soit $10$ $10$ . Ce résultat sera le numérateur de la réponse définitive ^{[1]
X
Source de recherche}.
- Autre exemple : trouvez le numérateur du produit ${\frac {3}{4}}\times {\frac {1}{3}}$ . Tout nombre multiplié par $1$ laisse ce nombre inchangé : le nouveau numérateur est donc $3$ ( $3\times 1$ ).
CONSEIL D'EXPERT(E)

Grace Imson, MA
Professeure de mathématiques au City College of San Francisco
Grace Imson est une professeure de mathématiques ayant plus de 40 ans d'expérience dans l’enseignement. Grace exerce actuellement au City College de San Francisco. Auparavant, elle était professeure au département de mathématiques de l'université Saint-Louis. Elle a enseigné cette discipline aux niveaux primaire, intermédiaire, secondaire et universitaire. Elle est titulaire d'un master en éducation avec une spécialisation en administration et supervision, délivré par l'université Saint-Louis.

Grace Imson, MA
Professeure de mathématiques au City College of San Francisco

Lorsque vous multipliez des fractions, multipliez toujours les nombres qui se font face. Multipliez les numérateurs de la première fraction et ceux de la seconde et écrivez les numérateurs des solutions. Faites ensuite la même chose avec les dénominateurs de vos fractions.
3
Calculez le dénominateur de la réponse. Comme précédemment, vous devez multiplier les dénominateurs des deux fractions. Dans l'exemple étudié, ${\frac {5}{6}}\times {\frac {2}{3}}$ ${\frac {5}{6}}\times {\frac {2}{3}}$ multipliez $6$ $6$ par $3$ $3$ , ce qui donne $18$ $18$ . C'est le dénominateur de la réponse définitive ^{[2]
X
Source de recherche}.
- Avec ${\frac {3}{4}}\times {\frac {1}{3}}$ , faites $4\times 3$ , ce qui donne $12$ , le dénominateur de la réponse définitive. La réponse est donc : ${\frac {3}{4}}\times {\frac {1}{3}}={\frac {3}{12}}$ .
4
Simplifiez la fraction trouvée. Vous devez donner comme réponse une fraction réduite à sa plus simple expression. Si le numérateur et le dénominateur ont un facteur commun, ils peuvent alors être divisés exactement par ce facteur et vous devez faire cette simplification. Le produit ${\frac {5}{6}}\times {\frac {2}{3}}$ ${\frac {5}{6}}\times {\frac {2}{3}}$ donne comme réponse : ${\frac {10}{18}}$ ${\frac {10}{18}}$ . $10$ $10$ et $18$ $18$ étant tous deux pairs, ils sont divisibles par $2$ $2$ . La réponse simplifiée est donc : ${\frac {5}{6}}\times {\frac {2}{3}}={\frac {5}{9}}$ ${\frac {5}{6}}\times {\frac {2}{3}}={\frac {5}{9}}$ ^{[3]
X
Source de recherche}.
- Simplifiez la fraction ${\frac {3}{12}}$ . Le numérateur et le dénominateur sont divisibles par $3$ , il est donc possible de simplifier et la réponse définitive est : ${\frac {1}{4}}$ .
Publicité

Méthode 2

Méthode 2 sur 3:
Multiplier des nombres fractionnaires

1
Inscrivez sur le papier toutes les étapes du calcul. Bien sûr, plus tard, vous pourrez faire les calculs de tête, mais au début, il vaut mieux tout écrire. Ainsi, si vous vous trompez, vous pourrez reprendre les différentes étapes, voir où vous avez commis une erreur et faire les corrections nécessaires.
- Les fractions présentent deux valeurs : le numérateur (le nombre du haut) et le dénominateur (le nombre du bas), séparés par un trait de fraction horizontal. Un nombre fractionnaire est composé d'une partie entière à gauche et d'une fraction à droite.
2
Transformez le nombre fractionnaire en une fraction impropre. Supposons que vous ayez à faire le produit $1\ {\frac {3}{4}}\times 7\ {\frac {1}{5}}$ $1\ {\frac {3}{4}}\times 7\ {\frac {1}{5}}$ . La première chose à faire est donc de transformer les deux nombres fractionnaires en fractions impropres, leurs numérateurs seront alors supérieurs à leurs dénominateurs ^{[4]
X
Source de recherche}.
- $1\ {\frac {3}{4}}$ est équivalent à ${\frac {7}{4}}$ . Lors de la transformation, le dénominateur reste le même, la partie entière se doit d'être multipliée par ce dénominateur ( $1\times 4$ ) et ramenée sur celui-ci ( ${\frac {4}{4}}$ ), puis vous additionnez les deux fractions :
  ${\frac {4}{4}}+{\frac {3}{4}}={\frac {7}{4}}$ .
- Pour le nombre $7\ {\frac {1}{5}}$ , multipliez la partie entière par le dénominateur de la partie fractionnaire ( $7\times 5$ ) et ramenez le tout sur le dénominateur, ce qui donne la fraction impropre ${\frac {35}{5}}$ à laquelle vous ajoutez ${\frac {1}{5}}$ pour obtenir ${\frac {36}{5}}$ .
3
Si c'est possible, simplifiez les fractions impropres. Reprenons l'exemple étudié, à savoir ${\frac {7}{4}}\times {\frac {36}{5}}$ ${\frac {7}{4}}\times {\frac {36}{5}}$ . Bien sûr, il est possible de multiplier les numérateurs et les dénominateurs, mais avant d'y procéder, voyez si une simplification est possible. Pour cela, voyez s'il n'existe pas un facteur commun aux numérateurs et aux dénominateurs, tous confondus. Ici, $7$ $7$ et $45$ $45$ ne peuvent être simplifiés, mais $36$ $36$ est multiple de $4$ $4$ , ce qui permet de simplifier par cette valeur ^{[5]
X
Source de recherche}.
- Divisez le dénominateur de ${\frac {7}{4}}$ par $4$ , ce qui donne $1$ , et vous obtenez la fraction simplifiée ${\frac {7}{1}}$ .
- Divisez le numérateur de ${\frac {36}{5}}$ par $4$ ce qui donne $9$ , et vous obtenez la fraction simplifiée ${\frac {9}{5}}$ .
- Une fraction est simplifiable s'il y a un facteur commun au numérateur et au dénominateur. Ainsi, si au lieu d'avoir ${\frac {7}{4}}$ , nous avions eu ${\frac {8}{4}}$ , cette fraction pouvait se simplifier par $4$ sous la forme ${\frac {2}{1}}$ .
4
Poursuivez les calculs. Vous devez à présent multiplier les numérateurs, puis les dénominateurs. Dans notre exemple, faites $7\times 9$ avec les numérateurs, soit $63$ , le numérateur de la réponse. Multipliez $1$ par $5$ et vous obtenez le dénominateur de la même réponse, soit $5$ . La réponse est donc : ${\frac {63}{5}}$ , laquelle est une fraction impropre ^{[6]
X
Source de recherche}.

Conseil : indiquez clairement les étapes du calcul afin de pouvoir vous y retrouver le cas échéant. Les nombres fractionnaires et les fractions impropres sont toujours un peu délicats à manipuler, et surtout la conversion entre les deux.
5
Transformez la réponse en un nombre fractionnaire. Le résultat est une fraction impropre qu'il faut transformer en nombre fractionnaire, et pour cela, il faut commencer par diviser le numérateur par le dénominateur. Dans l'exemple, divisez $63$ $63$ par $5$ $5$ , ce qui vous donne $12$ $12$ et un reste de $3$ $3$ . Ce $12$ $12$ sera la partie entière du nombre fractionnaire et le $3$ $3$ sera le numérateur de la partie fractionnaire. Quant au dénominateur, il est le même, à savoir $5$ $5$ . Le produit est le suivant :
$1\ {\frac {3}{4}}\times 7\ {\frac {1}{5}}=12\ {\frac {3}{5}}$ $1\ {\frac {3}{4}}\times 7\ {\frac {1}{5}}=12\ {\frac {3}{5}}$ ^{[7]
X
Source de recherche}.
- Si vous n'arrivez pas à faire la division de tête pour trouver la partie entière, faites-la par écrit.
Publicité

Méthode 3

Méthode 3 sur 3:
Multiplier des fractions avec une calculatrice

1
Transformez les fractions en nombres décimaux. Tapez vos fractions l'une après l'autre pour obtenir leurs équivalents en valeurs décimales. Pour calculer
$1\ {\frac {3}{4}}\times 7\ {\frac {1}{2}}$ $1\ {\frac {3}{4}}\times 7\ {\frac {1}{2}}$ , tapez sur la calculatrice la première fraction 3 ÷ 4 , ce qui donne
$0,75$ $0,75$ . Calculez ensuite la seconde fraction en tapant 1 ÷ 2, le résultat est $0,5$ $0,5$ ^{[8]
X
Source de recherche}.
- Certaines calculatrices permettent de rentrer sans difficulté les fractions sous la forme classique. Pour savoir si votre calculatrice accepte cette façon de présenter les fractions, consultez sa notice.
2
Transformez les nombres fractionnaires en nombres décimaux. La chose est très simple, quand bien même votre calculatrice n'aurait pas une fonction « fraction » spécifique. Commencez par calculer la valeur de la partie fractionnaire de votre nombre, comme dans l'étape précédente, puis ajoutez la partie entière ^{[9]
X
Source de recherche}.
- Pour avoir la valeur du nombre fractionnaire $3\ {\frac {3}{4}}$ , tapez sur votre calculatrice 3 ÷ 4 : $0,75$ s'affiche à l'écran. Ajoutez ensuite $3$ (+ 3), ce qui donne $3,75$ : votre nombre fractionnaire est désormais un nombre décimal.
3
Multipliez les valeurs décimales correspondantes. Vous avez noté sur le papier les deux valeurs décimales, multipliez-les à l'aide de la calculatrice. Reprenons l'exemple ${\frac {3}{4}}\times {\frac {1}{2}}$ ${\frac {3}{4}}\times {\frac {1}{2}}$ . Faites $0,75\times 0,5$ $0,75\times 0,5$ . Vous obtenez comme réponse $0,375$ $0,375$ . Toutes les étapes du calcul doivent être notées, Ainsi, en cas d'erreur ou de dysfonctionnement de la machine, vous n'aurez pas tout perdu ^{[10]
X
Source de recherche}.
- Si votre calculatrice gère les parenthèses, vous pouvez entrer toute l'opération d'une seule traite en tapant : (3/4)*(1/2). La touche / est celle de la division.
4
Convertissez les valeurs décimales en fractions. Sur votre feuille, notez une fraction qui aura pour numérateur le résultat et en dénominateur $1$ $1$ . Ici, vous écrirez ${\frac {0,375}{1}}$ ${\frac {0,375}{1}}$ . Multipliez le numérateur et le dénominateur par la puissance de 10 qui a autant de zéros que la réponse a de décimales, $0,375$ $0,375$ a trois chiffres après la virgule, vous devez donc multiplier la fraction par ${\frac {1\ 000}{1\ 000}}$ ${\frac {1\ 000}{1\ 000}}$ , la réponse définitive est la fraction : ${\frac {375}{1\ 000}}$ ${\frac {375}{1\ 000}}$ ^{[11]
X
Source de recherche}.
- Si votre calculatrice est dotée d'une fonction « fraction », utilisez-la pour convertir vos fractions. Consultez la notice de la machine.
5
Simplifiez la fraction finale. Face à une fraction obtenue par calcul, il faut toujours penser à la simplifier. Si les nombres de la fraction sont élevés, il faut songer que leur facteur commun est lui aussi élevé. Notre réponse est ${\frac {375}{1\ 000}}$ ${\frac {375}{1\ 000}}$ et à l'évidence, $5$ $5$ est un facteur commun. Simplification faite, ${\frac {375}{1\ 000}}={\frac {75}{200}}$ ${\frac {375}{1\ 000}}={\frac {75}{200}}$ . Cette fraction peut encore une fois être simplifiée par $5$ $5$ , ce qui donne : ${\frac {75}{200}}={\frac {15}{40}}$ ${\frac {75}{200}}={\frac {15}{40}}$ . Et elle se simplifie encore une fois par $5$ $5$ : ${\frac {15}{40}}={\frac {3}{8}}$ ${\frac {15}{40}}={\frac {3}{8}}$ ^{[12]
X
Source de recherche}.
- Au début, vous simplifierez ainsi, facteur après facteur, mais avec l'habitude, vous trouverez plus vite un plus grand facteur commun. Ici, il était de $125$ .
Publicité

Vidéo de wikiHow: Comment multiplier des fractions

Conseils

Quand, dans un exercice, vous avez des fractions qui sont additionnées, soustraites et multipliées, respectez bien l'ordre des opérations : parenthèses, multiplications et enfin, sommes. Si, par exemple, vous devez calculer ${\frac {7}{13}}+({\frac {5}{8}}\times {\frac {8}{9}})$ , faites d'abord le produit des parenthèses : ${\frac {5}{8}}\times {\frac {8}{9}}={\frac {40}{72}}$ , puis ajoutez ${\frac {7}{13}}$ .