Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 8 039 fois.
La résolution d'un polynôme de degré supérieur à 2 ressemble, dans le principe, à celle d'un polynôme du second degré dans la mesure où il faut dans un premier temps essayer de factoriser. Une fois le polynôme factorisé, il est alors simple d'en trouver les racines, valeurs pour lesquelles le polynôme s'annule. Il existe différentes méthodes pour résoudre ces polynômes du troisième degré () ou d'un degré supérieur. En fonction du polynôme proposé, une méthode est plus efficace qu'une autre : à vous de la deviner !
Étapes
Méthode 1
Méthode 1 sur 2:Savoir mettre en facteur un polynôme
-
1Si possible, factorisez le polynôme. Si les différents termes du polynôme ont en commun un facteur, faites la factorisation pour simplifier le problème. Ce ne sera pas toujours possible, mais il faut vérifier chaque fois.
-
1er exemple : trouvez les racines du polynôme .
Chaque terme étant divisible par , vous pouvez factoriser ainsi :
factorisez chaque terme, soit ,
mettez en facteur, soit .
À présent, résolvez l'équation entre parenthèses soit en factorisant à nouveau soit en utilisant le déterminant. Ici, on peut la factoriser sous la forme .
Les solutions sont : , et , soit , et .
-
1er exemple : trouvez les racines du polynôme .
-
2Identifiez les polynômes du second degré. Si vous savez résoudre les équations du second degré (), alors, vous savez résoudre toutes les équations qui se présentent sous la forme . Prenons quelques exemples.
-
2e exemple : résolvez .
Posez et vous obtenez : .
Trouvez en utilisant la méthode que vous voulez :
, ce qui donne ou .
Redonnez à sa valeur, soit : ou .
La première égalité () n'admet pas de solution, sauf si vous travaillez dans les complexes auquel cas x = ±i√2. Quant à la seconde égalité, elle donne deux solutions : x = ±√(2/3). - 3e exemple : l'équation ne peut être traitée de cette façon, mais vous remarquez qu'on peut mettre en facteur, ce qui donne : . Désormais, peut être transformée comme l'a été l'équation de l'exemple 2.
-
2e exemple : résolvez .
-
3Utilisez les identités remarquables des cubes. La somme ou la différence de cubes peut sembler étrange, mais en fait ils sont faciles à factoriser grâce aux identités remarquables.
- Somme des cubes : un polynôme de la forme se factorise sous la forme [1] .
- Différence des cubes : un polynôme de la forme se factorise sous la forme [2] .
- Notez que le polynôme entre parenthèses ne peut être factorisé [3] .
- Ces identités remarquables s'appliquent à tous les termes dont la puissance est multiple de 3, comme , …
-
4Voyez s'il y a moyen de factoriser le polynôme. La factorisation d'un polynôme est toujours loin d'aller de soi. Il faut se creuser la tête pour trouver un facteur commun. Pensez aussi à mettre en facteur des binômes, comme . Dans ces cas, il faut changer de place les différents termes pour trouver une factorisation partielle, puis globale [4] . Cette façon de faire n'est pas toujours possible. Essayez pendant quelques minutes, mais si rien ne ressort, abandonnez cette piste.
-
4e exemple : résolvez l'équation .
Au premier regard, on ne voit aucun facteur évident, mais si vous prenez en compte les deux premiers termes, vous voyez qu'on peut les factoriser :
.
Factorisez les derniers termes, soit , 2 étant le facteur commun :
.
Vous voyez que peut être mis en commun :
.
Publicité -
4e exemple : résolvez l'équation .
Méthode 2
Méthode 2 sur 2:Trouver une racine évidente et pratiquer la division synthétique
-
1Essayez de trouver une des racines du polynôme. La division synthétique ne peut être mise en œuvre que si vous arrivez à trouver une racine évidente. Dès lors, vous pourrez factoriser ce dernier. Cette racine peut être trouvée par tâtonnements ou par la méthode décrite précédemment. Si vous y arrivez, passez directement à la méthode de la division synthétique, sinon, il ne vous reste plus qu'à lire la méthode qui suit.
- La racine d'un polynôme est toute valeur de x pour laquelle le polynôme s'annule. Ainsi, si est une racine, vous pouvez mettre en facteur .
Essayer des racines évidentes
-
1Trouvez les facteurs de la constante du polynôme. Une racine évidente se trouve par tâtonnements successifs. Pour commencer, trouvez tous les facteurs de la constante [5] .
- Exemple : le polynôme a pour constante 9, dont les facteurs premiers sont : 1, 3 et 9.
-
2Faites la liste des facteurs du coefficient du premier terme. Ce coefficient est celui du terme qui est élevé à la plus forte puissance du polynôme. Listez ces facteurs sur une ligne différente de ceux trouvés précédemment.
- Exemple (suite) : le coefficient accolé au terme de plus forte puissance de est 2, dont les facteurs premiers sont : 1 et 2.
-
3Trouvez les racines éventuelles. Si le polynôme a une racine évidente, ce qui n'est pas forcément le cas, elle ne peut être que : ± (un des facteurs de la constante)/(un des facteurs du coefficient du terme de plus forte puissance). Si cette valeur satisfait l'équation à 0, nous l'appellerons c, vous pourrez mettre en facteur du polynôme de départ.
- Exemple (suite) : vous avez donc d'un côté trois facteurs pour la constante (1, 3 et 9) et de l'autre, deux facteurs pour le coefficient (1 ou 2). Selon ce principe, une des racines pourrait être un des nombres suivants : ±1/1, ±1/2, ±3/1, ±3/2, ±9/1 ou ±9/2. N'oubliez pas le signe « ± », puisque la solution est aussi bien positive que négative.
-
4Testez chacune de ces racines potentielles. Rien ne garantit qu'une valeur soit une racine, aussi devez-vous toutes les tester dans le polynôme de départ.
-
Exemple : 1 (1/1) est la première racine possible. Testez-la en remplaçant x par 1, ce qui vous donne le calcul suivant :
. Le résultat étant 0, la valeur 1 est alors considérée comme une racine du polynôme, ce qui signifie que vous pouvez factoriser le polynôme par . - Si aucune des racines potentielles ne convient, alors vous pourrez en conclure qu'il n'y a pas de racines évidentes et que vous ne pouvez pas factoriser pour l'instant.
Publicité -
Exemple : 1 (1/1) est la première racine possible. Testez-la en remplaçant x par 1, ce qui vous donne le calcul suivant :
Essayer la division synthétique
-
1Posez bien le problème. La division synthétique est une méthode pour trouver toutes les racines d'un polynôme, à condition que vous en connaissiez déjà une. Pour écrire la division, inscrivez la racine trouvée, puis tracez un petit trait vertical à droite. Inscrivez ensuite à droite les coefficients des différents termes, dans l'ordre décroissant des puissances. Seuls les coefficients nous intéressent ici, pas les termes entiers.
- Nota bene : si un terme venait à manquer (avec un coefficient nul), il faudrait le réintégrer. Ainsi, le polynôme devra être écrit ainsi : .
-
Exemple (suite) : suite au test effectué, vous avez trouvé que 1 était une des racines du polynôme .
Inscrivez alors 1 (la racine), puis un trait vertical, puis les coefficients du polynôme dans l'ordre :
-
2Abaissez le premier coefficient. Recopiez le premier coefficient à l'aplomb et deux lignes plus bas. Laissez une ligne entre les deux pour inscrire d'autres valeurs.
-
Exemple (suite) : inscrivez un autre 2 à l'aplomb du premier et deux lignes plus bas :
-
Exemple (suite) : inscrivez un autre 2 à l'aplomb du premier et deux lignes plus bas :
-
3Multipliez ce nombre par la racine trouvée. Notez la réponse sous le deuxième coefficient, mais sur la ligne intercalaire, laissée en blanc.
-
Exemple (suite) : multipliez le 2 du bas par la racine (1), ce qui fait 2. Notez 2 sous le deuxième coefficient (1), mais sur la ligne intercalaire :
-
Exemple (suite) : multipliez le 2 du bas par la racine (1), ce qui fait 2. Notez 2 sous le deuxième coefficient (1), mais sur la ligne intercalaire :
-
4Faites la somme de la colonne. Il s'agit de celle du deuxième coefficient qui contient à présent, calculs faits, deux chiffres l'un sous l'autre. Additionnez-les et inscrivez le résultat de l'opération sous ces chiffres, sur la ligne de la réponse.
-
Exemple (suite) : 1 + 2 = 3
-
Exemple (suite) : 1 + 2 = 3
-
5Multipliez ce résultat par la racine. Comme précédemment, multipliez le dernier résultat par la racine. Inscrivez votre réponse sous le coefficient suivant.
-
Exemple (suite) : 1 x 3 = 3
-
Exemple (suite) : 1 x 3 = 3
-
6Calculez la somme de colonne suivante. Comme précédemment, additionnez les deux nombres de la colonne suivante et inscrivez le résultat de l'opération sous ces nombres, sur la ligne de la réponse.
-
Exemple (suite) : -12 + 3 = -9
-
Exemple (suite) : -12 + 3 = -9
-
7Répétez le procédé. Répétez-le jusqu'à arriver à la dernière colonne. Le dernier nombre de la dernière colonne doit être 0. Si ce n'était pas le cas, ce serait parce que vous avez commis une erreur quelque part : vérifiez vos calculs.
-
Exemple (suite) : multipliez -9 par la racine (1), inscrivez le résultat au bas de la dernière colonne : celui-ci doit impérativement être 0 :
-
Exemple (suite) : multipliez -9 par la racine (1), inscrivez le résultat au bas de la dernière colonne : celui-ci doit impérativement être 0 :
-
8Utilisez la dernière ligne pour récrire le polynôme. Vous avez déjà une expression mise en facteur, à savoir le monôme , c étant une racine du polynôme. L'expression complémentaire est donnée par la dernière ligne de la fausse matrice : ce sont les nouveaux coefficients de x. Simplement, vous devrez abaisser les puissances d'un degré.
-
Exemple (suite) : la dernière ligne est la suivante : 2 3 -9 0, ce dernier zéro ne sera pas pris en compte.
Comme le premier terme du polynôme de départ était , le degré du premier terme de votre réponse est forcément inférieur de 1, soit . Votre premier terme est donc .
Abaissez d'une unité chaque puissance et vous obtenez : .
Le polynôme de départ () est factorisé sous la forme : .
-
Exemple (suite) : la dernière ligne est la suivante : 2 3 -9 0, ce dernier zéro ne sera pas pris en compte.
-
9Factorisez la dernière expression. Si le polynôme trouvé précédemment est du second degré et si c'est possible, factorisez ce polynôme, en utilisant une racine évidente ou le déterminant. Si le polynôme secondaire est d'un degré supérieur à 2 et si vous trouvez une nouvelle racine évidente, refaites une division synthétique.
- Souvenez-vous que la division synthétique ne peut être mise en œuvre que si vous avez déjà une racine du polynôme. Calculez les racines potentielles et testez-les. Si aucune ne satisfait le polynôme à 0, alors vous ne pouvez pas factoriser le polynôme.
-
Exemple (suite) : votre polynôme se présente désormais sous la forme . Essayez de lui trouver une racine évidente, la méthode de la division synthétique ou plus classiquement la méthode du déterminant.
Ici, une des racines est -3, le polynôme de départ devient : . Les racines du polynôme sont donc : , et .
Publicité
Conseils
- Les termes de racines, de zéros et de solutions font tous référence à la même chose : ce sont les valeurs pour lesquelles un polynôme s'annule.
- Il existe bien des formules pour trouver les racines d'un polynôme du troisième et du quatrième degré, mais elles sont très compliquées à mettre en œuvre, sauf si elles sont programmées sur une calculatrice ou un ordinateur. Quant aux polynômes d'un degré supérieur, il n'existe pas de formules toutes faites, vous devrez utiliser, par approches successives, une des méthodes exposées plus haut.
- La règle des signes de Descartes ne donne pas les racines, mais le nombre de racines positives possibles d'un polynôme à coefficients réels. La procédure doit se faire dans l'ordre [6]
.
- Classez le polynôme par ordre décroissant de puissance : .
- Ignorez les termes et n'inscrivez que les signes des coefficients (positifs ou négatifs). Ici, la séquence des signes est .
- Comptez le nombre de fois où le signe change ( laisse la place à et inversement) en allant de la gauche vers la droite : la séquence montre 2 changements de signe.
- Le nombre de racines peut être égal à ce résultat ou bien à ce résultat auquel on aurait retiré 2n, n étant un entier. Avec , il pourrait y avoir deux racines… ou aucune. Si avec un autre polynôme, vous aviez eu sept changements de signe, il aurait pu y avoir 7, 5, 3 racines ou encore une seule.
Avertissements
- Si vous obtenez une racine imaginaire, parce qu'on vous a demandé de résoudre le polynôme dans l'ensemble des complexes, n'oubliez pas que cette valeur est racine, mais également sa conjuguée. Si (x - 3i) est une racine, alors (x + 3i) en est aussi une.
Références
- ↑ https://www.khanacademy.org/math/algebra2/polynomial-functions/advanced-polynomial-factorization-methods/v/factoring-sum-of-cubes
- ↑ https://www.khanacademy.org/math/algebra2/polynomial-functions/advanced-polynomial-factorization-methods/v/difference-of-cubes-factoring
- ↑ http://www.purplemath.com/modules/specfact2.htm
- ↑ https://www.khanacademy.org/math/algebra2/polynomial-functions/advanced-polynomial-factorization-methods/v/factoring-5th-degree-polynomial-to-find-real-zeros
- ↑ http://www.purplemath.com/modules/rtnlroot.htm
- ↑ http://www.purplemath.com/modules/drofsign.htm

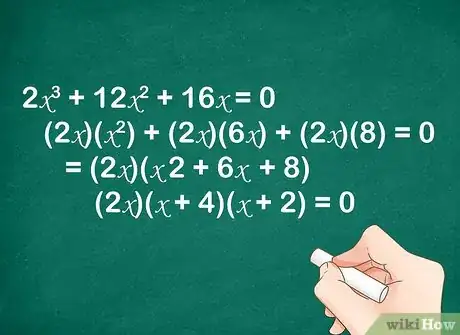











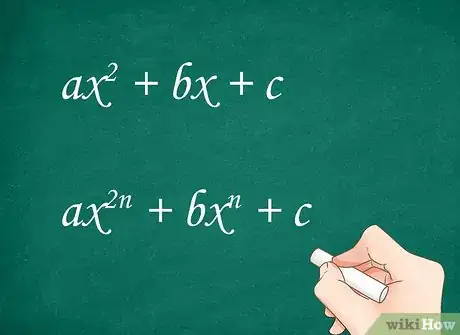























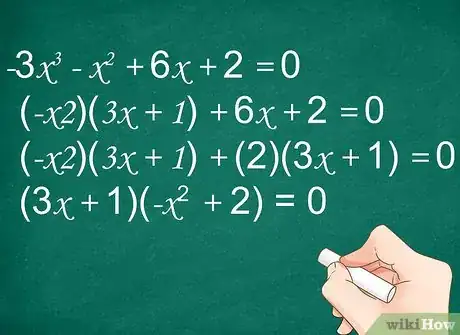







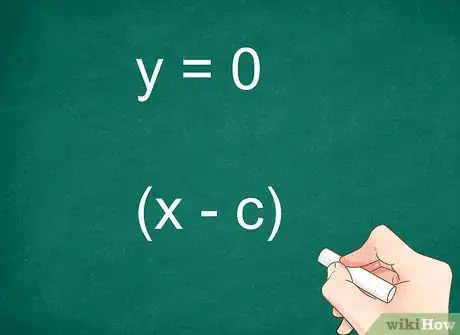









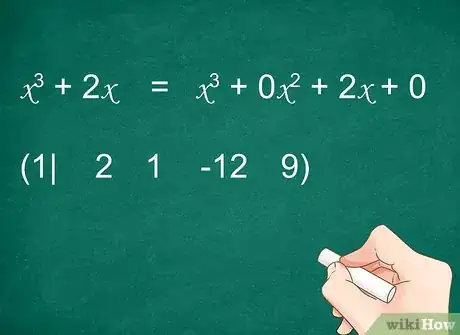





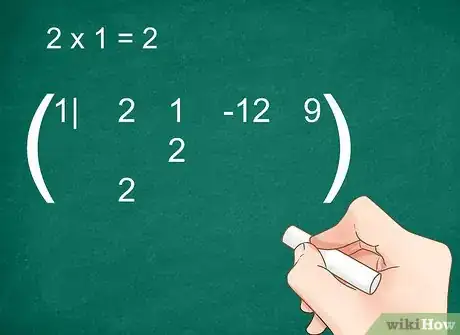

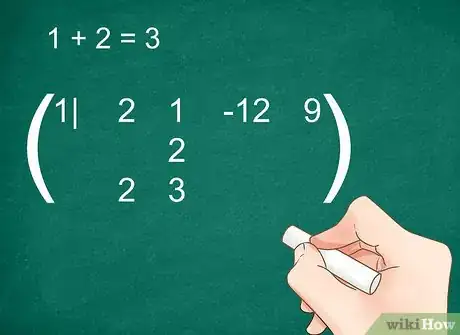





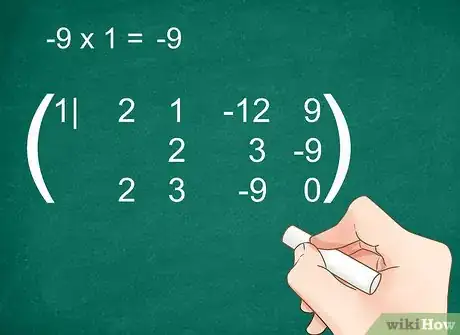

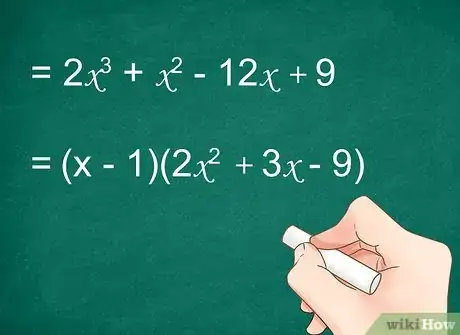



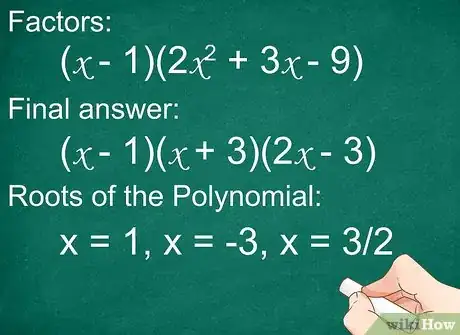




























L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 8 039 fois.