كوارك

الكوارك أو الرِكِّين هو جسيم أولي وأحد المكونين الأساسيين للمادة في نظرية النموذج القياسي لفيزياء الجسيمات (المكون الآخر حسب هذه النظرية هو الليبتونات) له كتلة ولكن أبعادها متناهية الصغر صفرية، تُرصَد عند حدوث تصادم شديد بين البروتون والإلكترون. أطلق موري جيلمان عليها الاسم كوارك ومنها ستة أنواع.

 كوارك

البروتون يتكون من كواركين علويين up وكوارك سفلي down.
التكوين جسيم أولي
العائلة فرميون
الجيل أول، ثاني، ثالث
التفاعل كهرومغناطيسية، جاذبية، قوي، ضعيف
جسيم مضاد مضاد الكوارك (
q
)
واضع النظرية موري جيلمان (1964)
جورج زفايج (1964)
المكتشف المختبر المسرّع الوطني (~1968)
الرمز
q
عدد الأنواع 6 (علوي، سفلي، ساحر، غريب، قمي، وقعري)
الشحنة الكهربائية +2⁄3 e, −1⁄3 e
شحنة لونية متواجدة
الدوران 1⁄2
رقم باريون 1⁄3

للكواركات جسيمات مضادة مثل بقية الجسيمات الأولية تدعى "كواركات مضادة"، حيث تتميز الكواركات والكواركات المضادة بأنها الجسيمات الوحيدة التي تتآثر مع بعضها باستخدام القوى الأربع الرئيسة الموجودة في الطبيعة. تشكل الكواركات معظم الجزء الداخلي للمادة، فالبروتون يتكون من ثلاث كواركات : u u d (أنظر الشكل للبروتون) ; و النيوترون مكون من ثلاث كواركات: d d u ، وهي مترابطة مع بعضها بقوى شديدة ويصعب فكها إلا في معجلات الجسيمات حيث تـُجرى تصادمات شديدة لفصلها عن بعض. هذه القوى التي تربط الكواركات مع بعضها البعض تدرس في فرع من الفيزياء يدعى ديناميكا لونية كمية (بالإنجليزية: Quantum-chromodynamic QCD)‏.

تجتمع الكواركات معا لتشكل جسيمات مركبة تسمى هادرونات، الأكثر استقرارا التي هي البروتونات والنيوترونات، وهي مكونات نواة الذرة.[1] لا يمكن أن تظهر الكواركات بشكل مفرد حر فهي دائمًا محتجزة ضمن هادرونات ثنائية (ميزونات) أو ثلاثية (باريونات) مثل البروتونات والنيوترونات،[2][3] وتسمى هذه الظاهرة بالحبس اللوني (بالإنجليزية: Color confinement)‏، لهذا السبب فمعظم المعلومات عن الكواركات تم استخلاصها من تجارب ومشاهدات على الهادرونات.

للكوارك ست أنواع وتسمى بالنكهات وهي: العلوي up، السفليdown، الساحر charm، الغريبstrange، القمي top، والقعريbottom.[4] كل من الكوارك العلوي والسفلي له كتلة أقل من باقي الكواركات الأخرى. فالكواركات الأثقل تتحول إلى علوية وسفلية بسرعة خلال عملية تسمى اضمحلال الجسيم: حيث تتحول حالة الكتلة الأثقل إلى حالة كتلة أخف. لهذا فالكوارك العلوي والسفلي هما الأكثر استقرارا ووجودا في الكون، في حين أن الكواركات المسماة بالساحر والغريب والقمي والقعري يتم إنتاجها فقط من خلال اصطدامات عالية الطاقة (مثل المستخدمة في معجلات الجسيمات أو ناتجة من الأشعة الكونية ).

لدى الكوارك خصائص أساسية مثل الشحنة الكهربائية والشحنة اللونية والدوران المغزلي والكتلة. فالكواركات هي الجسيمات الأولية الوحيدة في النموذج القياسي لفيزياء الجسيمات التي تُظهِر جميع القوى الأساسية الأربع المسماة بالتفاعلات الأساسية وهي الكهرومغناطيسية والجاذبية والقوة النووية القوية والضعيفة، بالإضافة إلى أنها الجسيمات الوحيدة التي لا تعد شحنتها الكهربائية مضاعفات صحيحة للشحنة الأولية. ولكل كوارك جسيم مضاد، وهو نظير مطابق له، لديه نفس قدر شحنة الكوارك ولكن بشحنة معاكسة.

كان ظهور نموذج الكوارك سنة 1964 بواسطة فرضية موري جيلمان وجورج سويج لشرح نماذج الهادرونات،[5] وقد كان هناك دليل ضعيف على وجودها المادي حتى سنة 1968.[6][7] تمت ملاحظة جميع نكهات الكوارك الست في تجارب المعجلات؛ وقد كان الكوارك القمي هو آخر ما تم اكتشافه من الكواركات وذلك سنة 1995 عندما تمت مشاهدته لأول مرة في معهد فيرميلاب.[5]

البداية
موري جيلمان في إحدى المؤتمرات سنة 2007. وهو الذي اقترح نموذج الكوارك مع جورج سويج سنة 1964.

قدم العالم الفيزيائي موري جيلمان مقترح نموذج الكوارك بشكل منفصل[8] إلى جانب جورج سويج[9][10] سنة 1964.[5] جاء المقترح بعد ظهور صيغة جيلمان الرياضية عن نظام تصنيف الجسيمات المسمى طريق الثمان لفات أو بمصطلح علمي أكثر، تناظر النكهة أس يو 3.[11] وقد قدم ايفال نعمان مشروع مشابه أكثر تطورا بقليل في نفس السنة.[12][13]

عندما اكتشفت الهادرونات، كان ينظر إليها على أنها مثل البروتونات ونيوترونات البيون، أي جسيمات أولية، لكن تم اكتشاف هادرونات جديدة فأصبحت من الكثرة أشبه بحديقة حيوان الجسيمات، فبعدما كانت عدة هدرونات خلال عقديّ الثلاثينات والأربعينات من القرن العشرين، صارت عدة عشرات في الخمسينات من ذات القرن، وكانت الروابط فيما بينها غير واضحة حتى سنة 1961 عندما افترض كلا من موري جيلمان وجورج سويج بأنهما ليست جسيمات أولية، ولكن بدلا من ذلك كانت تتألف من مزيج من الكواركات وضديدها. يشترك في نموذجهما ثلاث أنواع من الكواركات -كوارك علوي وسفلي وغريب- والتي نسباها إلى خصائص مثل اللف والشحنة الكهربائية.[8][9][10] وقد تباينت ردود الفعل للمقترح عند المجتمع الفيزيائي. كان هناك نوع من الخلاف حول ما إذا كان كوارك كيان مادي أو مجرد فكرة تستخدم لشرح مفاهيم لم تفهم بشكل جيد في ذاك الوقت.[14]

وفي أقل من سنة، ظهرت اقتراحات جديدة أضيفت لنموذج جيلمان-سويج. فافترض كل من جيمس بيوركن وشيلدون جلاشو بوجود نكهة لكوارك رابع، وسمي بالساحر. أضيف الاقتراح لأنه يسمح بالحصول على وصف أفضل للتفاعل الضعيف (وهي الآلية التي تسمح للكواركات بالتحلل)، فتساوي عدد كواركات مع عدد من اليبتونات، وهي لها صفة الكتلة فهي تنتج وبشكل صحيح كتل الميزونات.[15]

لم يظهر دليل مباشر على وجود الكواركات حتى تم اكتشافها سنة 1968 في مركز المعجل الخطي ستانفورد (بالإنجليزية: SLAC )‏. فتجربة التصادم غير المرن العميق (بالإنجليزية: Deep inelastic scattering)‏ أشارت إلى أن للبروتون بنية داخلية ، وأن البروتون مكون من نقاط صغيرة شبيهة بالأجسام، مما يعني بأنه ليس جسيم أولي (وهذا ما يشرحه نموذج الكواركات).[6][7][16] وأحجم الناس عن التعرف على تلك الأجسام ككواركات، مفضلين تسمية ريتشارد فاينمان لها بالبارتون وكان ذلك في بداية الأمر.[17][18][19] أمكن لاحقا تعريف تلك الجسيمات التي لوحظت في المختبر بأنها كواركات علوية وسفلية عندما تم اكتشاف نكهات أخرى معها.[20] ومع هذا فإن البارتون ظل مستخدما كمصطلح جماعي للجسيمات الأساسية للهادرون (الكواركات وضدائدها والغلوونات).

امكن تثبيت ظهور الكواركات الغريبة بطريقة غير مباشرة في المختبر المسرّع الوطني في تجربة التصادم غير المرن العميق: فهي لم تكن فقط العنصر الأساسي لنموذج الكواركات الثلاث لجيلمان وسويج، ولكنها أعطت تفسيرا للهادرونات المكتشفة في الأشعة الكونية سنة 1947 وهي كاون (
K
) والبيون (
π
).‏[21]

في سنة 1970 قدم كلا من جون ايليوبولوس وشيلدون جلاشو وماياني ورقة عرضت الكثير من الاستنتاجات في وجود كوارك لم يكتشف بعد ويسمى بالكوارك الساحر.[22][23] ثم ارتفع عدد الكواركات الافتراضية إلى ستة في سنة 1973، عندما لاحظ كلا من ماكوتو كوباياشي وتوشيهيده ماساكاوا في رصد لتجربة خرق تناظرالشحنة السوية[nb 1][24] بأنه يمكن تفسيرها إذا كان هناك زوجا إضافيا من الكواركات. وقد سمي هذا الزوج بكوارك قمي وقعري

تم إنتاج الكواركات الساحرة في نفس الوقت بشهر نوفمبر سنة 1974 — إحداهما عن طريق المختبر سالف الذكر على يد بورتون ريختر، والآخر في مختبر "BNL" على يد صموئيل تينج. للكواركات الساحرة المكتشفة حدود مع ضديد الكواركات الساحرة في داخل الميزون. فكلا الطرفين كان له ميزونات محددة برموز مختلفة، J وψ; وبذا فالميزون المشكل أصبحت تسميته بميزون
J/ψ
. وعندها فقط أقتنع مجتمع الفيزيائيين بصحة نظرية نموذج الكوارك.[19]

تمت ملاحظة الكوارك القعري في سنة 1977 بمختبر فيرميلاب عن طريق فريق بقيادة ليون ليدرمان.[25] وكانت تلك علامة قوية على وجود كوارك القمة: فعدم وجود كوارك القمة يعني بأن الكوارك القعري لن يكون له شريك. لكن لم يتم اكتشاف الكوارك القمي إلا سنة 1995 بواسطة فريق من مختبر فيرميلاب أيضا[5] حيث تبين أن له كتلة كبيرة جدا لم تكن متوقعة من قبل[26]— وهو تقريبا بحجم ذرة الذهب.[27]

التسمية

سمّى جيل مان الكوارك بهذا الاسم بعيد سماعه لصوت البط.[28] وقد استغرق بعض الوقت لصياغة التهجئة الصحيحة للمصطلح الجديد، حتى وجد كلمة كوارك "Quark" في كتاب جيمز جويس المسمى "استيقاظ فينغانز" (1939):

«Three quarks for Muster Mark

Sure he has not got much of a bark
And sure any he has it's all beside the mark.

»، جيمز جويس، استيقاظ فينغانز[29]

وقد أسهب جيلمان بتفاصيل أكثر عن مصطلح الكوارك في كتابه، "الكوارك والياغوار" (بالإنجليزية: The Quark and the Jaguar)‏.[30] أما سويج فقد فضل كلمة "ace-الآس" كمصطلح للجسيم الذي افترضه، لكن مصطلح جيلمان أخذ حظه من الشهرة بمجرد ماتم القبول بنموذج الكوارك.[31]

أما في اللغة العربية, فيُدعى الكوارك الرِّكِّين وهي من كلمة رُكن كناية عن كونه أحد الجسيمات البانية الذي يرتكن إليها بناء الجسيمات الأكبر منه كالبروتون.

للكواركات ست نكهات. تتعدد أسباب تسمية نكهاتها بمسمياتها الحالية، فمصطلح ركّين علوي وسفلي كان بسبب عناصر حمل اللف النظائري العلوية والسفلية،[32] والركّين الغريب فقد أعطي اسمه بسبب أنه قد تم اكتشافه ليكون من عناصر الجسيمات الغريبة المكتشفة في الأشعة الكونية قبل ظهور نموذج الرِّكينات بسنوات؛ فقد اعتبرت تلك الجسيمات «غريبة» لأن عمرها غير عادي وطويل جدا.[33] أما الركّين الفاتن فقد جائت تسميته بعدما اقتبس العالم جلاشو -وهو الذي افترض وجود هذا الركّين بالتعاون مع بيوركن- قائلا: "سوف نعطي منظومتنا لقب 'ركّين فاتن' لأننا مفتونون ومعجبون من التناظر الذي جيئ به من عالم دون الذرة".[34]" أما القمي والقعري فقد تم اختيار أسمائهم لأنهم "منطقيا شركاء للكواركات العلوية والسفلية"[33] وقد كانت مسمياتهم بالسابق هي "الحقيقة" (بالإنجليزية: Truth)‏ و"الجمال"' (بالإنجليزية: Beauty)‏ على التوالي، ولكن تم إلغائها من معجم المصطلحات الفيزيائية المستخدمة عند اختيار المسميات الجديدة.[35]

التصنيف
طالع أيضًا: النموذج القياسي
ست من الجسيمات في النموذج القياسي هي كواركات (تظهر باللون البنفسجي) وكل عمود من الأعمدة الثلاثة المرقمة (I و II و III) يمثل جيل للمادة.

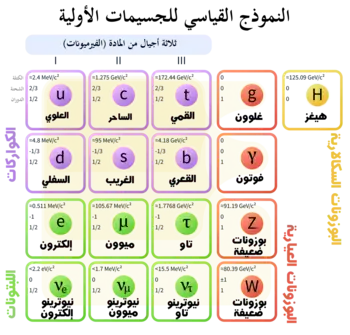
يعتبر النموذج القياسي الإطار النظري الذي يعطي وصفا لجميع الجسيمات الأولية المعروفة حاليا، فضلا عن بوزونات هيغز.[nb 2] المخفية[36] فهذا النموذج يحتوي على ست نكهات من الكواركات ورمزها: (
q
)، وهي الكوارك العلوي (
u
)، والسفلي (
d
)، والفاتن (
c
)، والغريب (
s
)، والقمي (
t
)، وأخيرا القعري[4] (
b
). تسمى الأجسام المضادة للكواركات بضديد الكوارك ويرمز لها بخط فوق رمز الكوارك المطابق، مثل
u
 لضديد الكوارك العلوي. وكما هو حال المادة المضادة بشكلها العام، فإن ضديد الكوارك له نفس الكتلة، ومتوسط العمر واللف الذي يوجد بالكوارك، ولكنه معاكس بالشحنة الكهربائية والشحنات الأخرى.[37]

الكوارك هو جسيم ذو دوران مغزلي -1⁄2، مما يعني ضمنا أنه فرميون حسب مبرهنة إحصاء اللف. وتلك تكون خاضعة لمبدأ استبعاد باولي، والتي تقول بأنه لايمكن لأكثر من فرميون أن يحتل حيزا في نفس الحالة الكمومية. وهو على النقيض من بوزونات (وهي جسيمات لها عدد صحيح باللف)، التي يمكن أن يكون أي كمية منها في نفس الحالة.[38] وخلافا للبتونات، فالكواركات تستحوذ على الشحنة اللونية، التي تجعلها تنخرط في التفاعل القوي. فبسبب التجاذب بين الكواركات المختلفة، تتشكل جسيمات مركبة تسمى بالهادرونات.

يحدد الكوارك الأرقام الكمية للهادرونات وتسمى بتلك الحالة كوارك مكافئ؛ وبصرف النظر عن هذا، فإن الهادرون قد يحتوي على عدد غير محدد من الكواركات الافتراضية (أو بحر) وضديدها الغلوونات التي لاتؤثر على أرقامها الكمية.[39] وهناك عائلتين من الهادرونات؛ الباريونات وبها ثلاث كواركات مكافئة، والميزونات وبها كوارك مكافئ مع ضديد الكوارك.[40] وأشهر الباريونات قاطبة البروتون والنيوترون، وهما أعمدة الأساس لنواة الذرة.[41] معظم الهادرونات معروفة، وأغلبها متباينة بما تحتوي من الكوارك والخصائص التي تضفيها كواركاتها الأساسية. أما وجود هادرونات شاذة مع مزيد من كواركات مكافئة، مثل التترا كواركات (
q

q

q

q
) والبنتا كواركات (
q

q

q

q

q
) فقد تم تخمينه،[42] ولم يتم اثبات وجوده حتى اليوم.[nb 3][42][43]

تنقسم الفرميونات الأولية إلى ثلاث أجيال فيزيائية، يحتوي كل جيل منها على اثنين من اللبتونات واثنين من الكواركات. والجيل الأول يحتوي على كواركات علوية وسفلية، والثاني يضم الكوارك الساحر والغريب، أما الجيل الثالث فيحتوي على الكوارك القمي والقعري. وقد فشلت جميع المحاولات والأبحاث لإيجاد جيل رابع من الكواركات أو فرميونات أولية،[44] وقد كانت هناك علامات غير مباشرة ولكن قوية للإيحاء بعدم وجود أكثر من ثلاث أجيال.[nb 4][45] تكون الأجيال الأعلى من الكواركات أكير كتلة وأقل ثباتا، مسببة بتحلل الكوارك إلى جسيمات الجيل الأدنى عن طريق تفاعلات ضعيفة. أما الذي يحدث بشكل عام في الطبيعة هو الجيل الأول (العلوي والسفلي). فالكواركات الثقيلة لا تنشأ إلا في تصادمات عالية الطاقة (مثل تلك المرتبطة بالأشعة الكونية)، ثم تضمحل بسرعة؛ مع ذلك فهناك اعتقاد سائد بأنها كانت موجودة بالجزء الأول من الثانية الأولى بعد حدوث الانفجار العظيم، عندما كان الكون في حالة حرارة وكثافة قصوى (ويسمى بعصر الكوارك). لذا فدراسة الكواركات الثقيلة تجري دائمًا في ظروف صناعية، مثل معجلات الجسيمات[46]

بما أن للكواركات شحنة كهربائية وشحنة لونية وكتلة ونكهة، لذا فهي الجسيمات الأولية الوحيدة المعروفة التي تتشارك في القوى الأساسية الأربع في الفيزياء المعاصرة: الكهرومغناطيسية، الثقالة أو الجاذبية، القوة النووية القوية، ثم القوة النووية الضعيفة.[41] وعلى الرغم من ذلك، فالجاذبية عادة لا علاقة لها مع المستويات دون الذرية، وليس لها وصف بالنموذج القياسي.

الخصائص

الشحنة الكهربائية
طالع أيضًا: شحنة كهربائية

قيم الشحنة الكهربائية الكسرية للكوارك تكون إما −1⁄3 أو +2⁄3 من قيمة الشحنة الأولية حسب النكهة. فالكواركات العلوية والساحرة وكواركات القمة (تعتبر كمجموعة كواركات العلوية) لها شحنة +2⁄3، بينما الكواركات السفلية والغريبة والقعريّة (كواركات المجموعة السفلية) لها −1⁄3. ضديد الكوارك لها الشحنة المعاكسة للكوارك المطابق لها؛ بمعنى شحنة ضديد كواركات المجموعة العلوية هي −2⁄3، وشحنة ضديد كواركات المجموعة السفلية تكون +1⁄3. بما أن الشحنة الكهربائية للهادرون هي مجموع شحنات الكواركات الأساسية، فعليه تكون شحنة الهادرونات عددا صحيحا: فشحنة تمازج ثلاث كواركات (باريون)، وثلاث ضديد كواركات (ضديد باريون)، أو كوارك وضديد كوارك (ميزون) تكون نتيجتها دائمًا عدد صحيح.[47] فعلى سبيل المثال، الهادرون عنصر أساسي في نواة الذرة، شحنة النيوترونات والبروتونات تكون 0 و+1 بالترتيب؛ يتكون النيوترون من كواركين سفليين وكوارك علوي واحد، والبروتون يحتوي كواركين علويين وكوارك سفلي واحد.[41]

لف مغزلي
طالع أيضًا: لف مغزلي (فيزياء)

اللف المغزلي هي خاصية جوهرية للجسيمات الأولية، واتجاهها هو درجة الحرية المهمة. وتُصور أحيانا كدوران الجسم حول محوره، وهذا المفهوم مضلل نوعا ما في جداول تحت الذرية لأنه يعتقد بأن الجسيم الأولي هو جسيم نقطي نوعا ما.[48]

يمثل اللف المغزلي بواسطة متجه ويقاس طوله بوحدة خفض ثابت بلانك ħ (تنطق خط هاء "h bar"). في الكوراكات قياس متجه عنصر اللف المغزلي حول أي محور لا يسفر إلا على القيم التالية +ħ/2 or −ħ/2; لهذا السبب فالكواركات تصنف كجسيمات لف مغزلي-1⁄2‏.[49] يرمز لعنصر اللف المغزلي حول محور معين -ويعرف بالمحور السيني- برمز سهم علوي ↑ للقيمة +1⁄2 وسهم سفلي ↓ للقيمة −1⁄2، ويوضع بعد شارة النكهة. فعلى سبيل المثال، يرمز لكوارك علوي بلف +1⁄2 حول المحور السيني بالرمز u↑‏.[50]

قوة نووية ضعيفة
المقالة الرئيسة: قوة نووية ضعيفة
مخطط فاينمان لتحلل بيتا مع اتجاه الزمن للأعلى. ترمز مصفوفة CKM إلى الاحتمالية لذلك وأيضا تحلل الكواركات الأخرى.

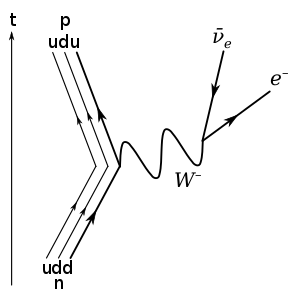
لا تتحول نكهة كوارك إلى نكهة آخرى إلا عن طريق القوة النووية الضعيفة، أحد القوى الأساسية في فيزياء الجسيمات، وذلك بواسطة امتصاص أو انبعاث بوزون و، حيث يصبح بالإمكان لكوارك من المجموعة العلوية (علوي، ساحر، قمي) الانتقال إلى كوارك المجموعة السفلية (سفلي، غريب، قعري) والعكس صحيح. فميكانيكية تحويل تلك النكهة تسبب عملية نشاط إشعاعي لتحلل البيتا، حيث ينشطر النيوترون (
n
) إلى بروتون (
p
) وإلكترون (
e−
) ونيوترينو إلكتروني مضاد (
ν
e). وتحدث تلك عندما يتحلل أحد الكواركات السفلية في النيوترون (
u

d

d
) إلى كوارك علوي بواسطة بعث بوزون
W−
 الافتراضي ومحولا النيوترون إلى بروتون (
u

u

d
). فيتحلل بعدها بوزون
W−
 إلى إلكترون و نيوترينو إلكتروني مضاد (
ν
e).[51]


n
←
p
 +
e−
 +
ν
e		(تحلل البيتا، رموز مجموعة الهادرون)

u

d

d
←
u

u

d
 +
e−
 +
ν
e		(تحلل البيتا، رموز مجموعة الكوارك)

ملحوظة: توجد صعوبة أحيانا في نقل المعادلات الإنجليزية إلى العربية ، فهنا اقترنت e مع p ولكنها تنتمي إلى
ν
e ، كذلك في المعادلة الثانية اقترنت الـ e مع uud , ولكنها تتبع النيوتربنو الإلكتروني المضاد
ν
e.

تستخدم كلا من عملية تحلل البيتا وعكسهاــ وهي عملية انعكاس تحلل بيتا ــ في المجالات الطبية مثل التصوير المقطعي بالإصدار البوزيتروني (PET) والتجارب عالية الطاقة مثل كشف النيوترينو.

قوة القوة النووية الضعيفة مابين الكواركات الست. تتحدد كثافة الخطوط بواسطة عناصر "مصفوفة CKM".‏

بما أن عملية انتقال النكهة هي نفسها لكل الكواركات، فكل كوارك له الأفضلية بالانتقال إلى كوارك آخر من نفس جيله. فالميول النسبية لجميع تحويلات النكهات مذكورة في جدول رياضي، يسمى مصفوفة كابيبو-كوباياشي-ماسكاوا (بالإنجليزية: Cabibbo–Kobayashi–Maskawa matrix)‏ ‏(CKM matrix). فالمقادير التقريبية لإدخالات "مصفوفة سي كي ام" هي كالتالي:[52]

حيث V'ij تظهر ميل كوارك النكهة i للتحول إلى كوارك النكهة j (والعكس صحيح).[nb 5]

يوجد مايعادل مصفوفة القوة النووية الضعيفة للبتونات (يمين بوزون و في الرسم البياني لتحلل البيتا)، وتسمى مصفوفة PMNS (بالإنجليزية: PMNS matrix ,Pontecorvo–Maki–Nakagawa–Sakata matrix)‏‏.[53] فكلا المصفوفتين (سي كي أم) و(بي أم أن أس) تشرحان جميع تحولات النكهات، ولكن لم تتضح الوصلات فيما بينهما حتى الآن.[54]

التآثر القوي والشحنة اللونية
طالع أيضًا: شحنة لونية وتآثر قوي
إجمالي الشحنة اللونية لكل الهادرونات يساوي صفر.

يمتلك الكوارك خاصية تسمى الشحنة اللونية. وتتكون تلك الشحنة من ثلاث أنواع، سميت عشوائيا بالأزرق والأخضر والأحمر.[nb 6] لكل نوع من تلك الأنواع مكمل من ضديد اللون - ضديد الأزرق، ضديد الأخضر، وضديد الأحمر. فإذا كان الكوارك يحمل لونا ما، فإن ضديد الكوارك يحمل ضديد اللون.[55]

يعبأ نظام التجاذب والتنافر فيما بين الكواركات بتركيبات مختلفة من الألوان الثلاثة ويسمى التفاعل القوي، وهو يتوسط قوة تحمل الجسيمات وتسمى بالغلوونات. فالنظرية التي تشرح التفاعلات القوية هي ديناميكا لونية كمومية (بالإنجليزية: QCD)‏ اختصارا. يشحن الكوارك بقيمة لونية واحدة يمكن أن تشكل نظام حاجز مع الكوارك المضاد له الحامل لضديد اللون المطابق؛ ثلاث من مضاد الكواركات كل منها له ضديد اللون، سيكون لها نظام حاجز مماثل. فعند جذب كواركين يكون الحاصل هو لون محايد: فمثلا كوارك له شحنة لون ξ مع ضديد كوارك له شحنة لون -ξ فالناتج هو شحنة لونية 0 (أو اللون الأبيض) فيتشكل الميزون بالتالي. فالمماثل لنموذج اللون الجمعي في علم البصريات، هو الجمع لكواركات ثلاث أو ضديد الكواركات كل منهم له شحنة لون مختلفة، ليكون الحاصل هو نفس شحنة اللون الأبيض مع تشكيل للباريون أو ضديد الباريون.[56]

في فيزياء الجسيمات الحديثة، فإن التناظر القياسي -هو أحد أنواع مجموعة التناظر- يصل ما بين تفاعلات الجسيمات. شحنة اللون (3)‏SU وهو تناظر قياسي يربط ما بين شحنة اللون في الكوارك والتناظر الظاهر في ديناميكا لونية كمومية.[57] كما أن قوانين الطبيعة تكون مستقلة عن الاتجاهات التي يتم تحديدها في فضاء س، ص، ع، ولا تتغير إذا استدارت محاور التنسيق إلى وجهة أخرى، ففيزياء ديناميكا لونية كمومية مستقلة عن اتجاه فضاء اللون ثلاثي الأبعاد والمعرف بالأحمر والأزرق والأخضر. يتطابق تحول اللون c‏(3)‏SU مع دوران في فضاء اللون (والتي تسمى رياضياتيا بالفضاء المركب (بالإنجليزية: complex space)‏. لكل نكهة كوارك f مطابق فرعي لألوان الكوارك fB، fG، fR‏،[58] تشكيل ثلاثي: ثلاثة عناصر مجال كمي والتي تتحول تحت تمثيل c‏(3)‏SU الأساسي.[59] فالشرط ليكون c‏(3)‏SU موضعي— أي؛ أن تسمح تحولاتها بالتغير حسب المساحة والزمن— يحدد خصائص التفاعل القوي، لا سيما في وجود ألوان غلوون الثمانية بصفتها حوامل القوة.[57][60]

الكتلة
طالع أيضًا: كتلة

يستخدم مصطلحين للإشارة إلى كتلة الكوارك: كتلة كوارك جاري وتشير إلى كتلة الكوارك ذاته، وكتلة كوارك أساسي وتشير إلى كتلة الكوارك مع كتلة مجال جسيم الغلوون المحيط بالكوارك.[61] وعادة ما يكون الاختلاف في قيم تلك الكتل كبيرا. فمعظم كتل الهادرونات تأتي من الغلوونات التي تربط الكواركات الأساسية ببعضها البعض، بدلا من الكواركات نفسها. وبما أن الغلوونات بطبيعتها تكون عديمة الكتلة، إلا أنها تمتلك طاقة أكبر—بشكل أدق طاقة ربط ديناميكا لونية كمومية (QCBE)—وهذا الذي يساهم إلى حد كبير في الكتلة الكلية للهادرون. فعلى سبيل المثال، كتلة البروتون تساوي 938 MeV/c2، من كتلة المتبقية حيث تسهم الكواركات الثلاث المكافئة بحوالي 11 MeV/c2 فقط؛ ويمكن أن يعزى الكثير من الكمية المتبقية إلى طاقة ربط الغلوونات QCBE‏.[62][63]

يفيد النموذج القياسي بأن كتلة الجسيمات الأولية تستمد من آلية هيغز، ذات الصلة ببوزون هيغز الافتراضي. ويأمل الفيزيائيون بأن مزيدا من الأبحاث عن أسباب ضخامة كتلة كوارك القمة، والتي وجد أنها تعادل نواة الذهب (~171 GeV/c2)‏،[62][64] قد تكشف عن مزيد من المعلومات عن نشأة كتل الكواركات وغيرها من الجسيمات الأولية.[65]

جدول الخصائص
طالع أيضًا: نكهة (فيزياء الجسيمات)

يلخص الجدول التالي خصائص للكواركات الست. نكهات أعداد الكم وهي: (اللف النظائري (I3)، السحر (C)، الغرابة (S)، القمة (T)، وأخيرا القعر (B‏′)) قد اسندت إلى بعض نكهات الكوارك، وللدلالة على جودة النظم القائمة على الكوارك والهادرونات. فرقم باريون (B) هو +1⁄3 لجميع الكواركات، لأن الباريون مكون من 3 كواركات. أما بالنسبة لضديد الكوارك فإن الشحنة الكهربائية (Q) وجميع نكهات أعداد الكم ("B" ،"I3" ،"C" ،"S" ،"T"، و"B‘") لديها الإشارة المعاكسة. الكتلة والزخم الزاوي الكلي ("J"؛ تساوي لف الجسيمات النقطية) لذا فإن إشارتها لا تتغير عند ضديد الكوارك.

خصائص نكهة الكوارك[62]
الاسم الرمز كتلة (إلكترون فولت)* J B Q I3 C S T B′ جسيم مضاد رمز الجسيم المضاد
الجيل الأول
علوي
u
 1.5 إلى 3.3 1⁄2 +1⁄3 +2⁄3 +1⁄2 0 0 0 0 ضديد علوي
u
سفلي
d
 3.5 إلى 6.0 1⁄2 +1⁄3 −1⁄3 −1⁄2 0 0 0 0 ضديد سفلي
d
الجيل الثاني
ساحر
c
 1270+70
−110		 1⁄2 +1⁄3 +2⁄3 0 +1 0 0 0 ضديد ساحر
c
غريب
s
 104+26
−34		 1⁄2 +1⁄3 −1⁄3 0 0 −1 0 0 ضديد غريب
s
الجيل الثالث
قمة
t
 171200±2100 1⁄2 +1⁄3 +2⁄3 0 0 0 +1 0 ضديد القمة
t
قعر
b
 4200+170
−70		 1⁄2 +1⁄3 −1⁄3 0 0 0 0 −1 ضديد القعر
b
J == زخم زاوي كلي، B = رقم باريون، Q = شحنة كهربائية، I3 = لف نظائري، C = السحر، S = الغرابة، T = القمة، B′ == القعر.
* الترميز مثل 4200+170
−70 تشير إلى قياسات غير متيقن بها.

كواركات متفاعلة
طالع أيضًا: حجز اللون وغلوون

كما في وصف الديناميكا اللونية الكمومية، فإن التآثر القوي يتوسط الكواركات بواسطة الغلوونات، وبوزونات قياسية ناقلة عديمة الوزن. كل غلوون يحمل شحنة لونية واحدة وشحنة ضديد اللون. ففي إطار العمل المقياسي لتفاعلات الجسيمات (وهو جزء من صياغة عامة تعرف بنظرية الاضطراب) فإن الغلوونات تنتقل باستمرار ما بين الكواركات خلال عملية انبعاث وامتصاص افتراضية. فعندما يتحول الغلوون ما بين الكواركات، فإنه يحدث تغير باللون في كلا الطرفين، فعلى سبيل المثال: عندما يبعث الكوارك الأحمر غلوون أحمر-ضديد أخضر، فإنه سيصبح أخضر، وأيضا عندما يمتص الكوارك الأخضر غلوون أحمر-ضديد أخضر، فإنه سيصبح كوارك أحمر. لذا بما أن كل لون كوارك يتغير بسرعة فإن التآثر القوي في ما بينهم لا يتأثر.[66][67][68]

وحيث أن الغلوونات تحمل شحنة لونية، فإن لها القدرة على بعث أو امتصاص الغلوونات الأخرى. وتسبب تلك ما يسمى بالحرية المتقاربة (بالإنجليزية: Asymptotic freedom)‏: وبما أن الكواركات تتقارب جدا من بعضها البعض فإن ذلك يضعف من قوة الربط للديناميكا اللونية بينها،[69] والعكس صحيح، فكلما تباعدت الكواركات عن بعضها فإن قوة الربط تزداد. فالمجال اللوني سيتعرض للإجهاد، اشبه بشريط مطاطي عند سحبه، فلتقوية هذا المجال ينشأ تلقائيا كمية غلوونات أكثر للألوان الملائمة. ويحدث إنتاج زوج كوارك وضديدها عند بداية حاجز الطاقة. فيتم فصل أزواج كواركات عن بعضها البعض متسببة بتشكيل هادرونات جديدة. وتعرف هذه الظاهرة باسم حجز اللون: فلا يمكن ظهور الكواركات بشكل منفرد.[70][71] تكون عملية تشكيل الهادرونات، التي تحدث قبل تشكيل الكواركات عند حالات الاصطدام عالية الطاقة، تكون قادرة على التفاعل بأي طريقة أخرى، ولكن يستثنى منها كوارك القمة، الذي يتحلل قبل أن يتهادرن.[72]

بحر الكواركات

تحتوي الهادرونات التي تساهم مع الكوارك المكافئ (
q
v) في أعداد الكم على أزواج كوارك-ضديد كوارك افتراضية (
q

q
) معروفة باسم "بحر الكواركات" (
q
s). ويتشكل بحر الكواركات من تصدع غلوونات مجال لون الهادرونات؛ ويمكن أن تتفاعل تلك العملية أيضا في الاتجاه المعاكس حيث أن إفناء اثنين من بحار الكواركات ينتج غلوون. فتكون النتيجة هي التدفق المستمر للغلوونات المجزأة المكونة لهذا "البحر".[73] يقل استقرار تلك البحار بكثير عن نظرائها المكافئة، وهي تفني بعضها البعض ضمن الأجزاء الداخلية للهادرون. لكن على الرغم من ذلك بإمكان بحر الكوارك أن تتهادرن إلى جزيئات باريونية أو ميزونية في ظروف معينة.[74]

مراحل أخرى لمسألة الكوارك
تقديم نوعي للرسم التخطيطي لمادة كوارك. والتفاصيل الدقيقة للمخطط موضوع البحوث الجارية.[75][76]

تتحرر الكواركات في الظروف القصوى وتظهر كجسيمات حرة. ففي سياق التقارب الحر فإن التآثر القوي يكون ضعيفا في درجات الحرارة العالية. وبالنهاية يختفي حجز اللون وتتشكل بلازما ذات حرارة عالية من الكواركات والغلوونات حرة الحركة. وتسمى تلك المرحلة النظرية للمادة باسم بلازما كوارك-غلوون.[77] ولا يعرف ماهية الظروف اللازمة التي تؤدي إلى إنشاء تلك الحالة، وإن كان موضوعا لقدر كبير من التخمينات والتجارب. فالتقييم الحالي قدر درجة الحرارة اللازمة بحوالي (1.90±0.02)×1012 كلفن.[78] لكن لم يتم الحصول على حالة كاملة من الكواركات أو الغلوونات الحرة (على الرغم من تعدد المحاولات في سيرن خلال عقد الثمانينات والتسعينات من القرن العشرين).[79] وقد أسفرت التجارب الحديثة في مصادم الأيون الثقيل النسبي مصادم ايونات ثقيلة بسرعات النسبية عن شواهد لحالة شبيه سائل الكوارك تكشف عن حركة سوائل شبه مثالية.[80]

تتميز بلازما كوارك-غلوون بزيادة كبيرة في عدد أزواج الكواركات الثقيلة مقارنة بعدد أزواج الكواركات العلوية والسفلية. وهناك اعتقاد أنه في الفترة التي سبقت 10−6 ثوان بعد الانفجار العظيم (حقبة الكوارك) بأن الكون امتلأ من بلازما كوارك-غلوون، حيث درجات الحرارة مرتفعة جدا للهادرونات كي تستقر.[81]

نظرا للكثافة الباريونية العالية ودرجات الحرارة المنخفضة نسبيا -مقارنة مع ما هو موجود بالنجوم النيوترونية- يُتوقع أن تتحلل حالة الكوارك إلى سائل فيرمي لكواركات التفاعل الضعيف. ويتميز هذا السائل بواسطة تكثيف الأزواج المساهمة للكوارك الملون، وبالتالي يكسر التناظر الداخلي SU(3)c. وبما أن الأزواج المساهمة للكوارك تأوي شحنة اللون، ففي تلك المرحلة لحالة الكوارك سيكون لديها توصيل فائق للون؛ لذا فإن شحنة اللون ستمر خلالها بدون أي عوائق.[82]

ملاحظات
  1. إن خرق تناظرالشحنة السوية هو عبارة عن ظاهرة تجعل التفاعلات الضعيفة تظهر بشكل مختلف عند حصول التكافؤ وتغيّر موضع الجزيئات وأضدادها.
  2. اعتبارًا من يوليو 2009.
  3. يزعم عدد من الباحثين أنه أثبت وجود التترا كواركات والبنتا كواركات خلال السنوات الأولى من القرن الحادي والعشرين. وعلى الرغم من أن وجود التترا كواركات ما زال موضع جدل بين العلماء، إلا أن جميع الجسيمات التي كان يُعتقد بأنها تشكل بنتا كواركات ثبت عدم وجودها.
  4. إن الدليل الأساسي الذي يدعم هذا القول يستند إلى عرض الصدى الخاص ببوزونات
    Z0
    ، التي لا تسمح لنوترينو الجيل الرابع أن يستحوذ على كتلة تفوق ~45 GeV/c2. وهذا الأمر يتناقض بشدة مع نوتريونات الأجيال الثالثة الأخرى، التي لا تستطيع كتلتها أن تزيد عن 2 MeV/c2.
  5. يعتبر الاحتمال الحقيقي لتحلل كوارك إلى إلى كوارك آخر مهمة معقدة (من بين المتغيرات الأخرى): تحلل كتلة الكوارك، كتل نواتج الإضمحلال، والعنصر المطابق لمصفوفة سي كي أم. تلك الاحتمالية تتناسب طرديا (لكن لا تساوي) مع مقدار مربع السي كي أم المطابقة.
  6. على الرغم من التسمية، إلا أن شحنة اللون لا علاقة لها بألوان الطيف الضوء المرئي.

اقرأ أيضا

المصادر
  1. "Quark (subatomic particle)"، موسوعة بريتانيكا، مؤرشف من الأصل في 7 مايو 2015، اطلع عليه بتاريخ 29 يونيو 2008.
  2. R. Nave، "Confinement of Quarks"، هايبرفيزيكس، جامعة ولاية جورجيا, Department of Physics and Astronomy، مؤرشف من الأصل في 16 مايو 2019، اطلع عليه بتاريخ 29 يونيو 2008.
  3. R. Nave، "Bag Model of Quark Confinement"، هايبرفيزيكس، جامعة ولاية جورجيا, Department of Physics and Astronomy، مؤرشف من الأصل في 1 مايو 2019، اطلع عليه بتاريخ 29 يونيو 2008.
  4. R. Nave، "Quarks"، هايبرفيزيكس، جامعة ولاية جورجيا, Department of Physics and Astronomy، مؤرشف من الأصل في 16 مايو 2019، اطلع عليه بتاريخ 29 يونيو 2008.
  5. B. Carithers, P. Grannis (1995)، "Discovery of the Top Quark" (PDF)، Beam Line، مركز المعجل الخطي ستانفورد، 25 (3): 4–16، مؤرشف من الأصل (PDF) في 3 ديسمبر 2016، اطلع عليه بتاريخ 23 سبتمبر 2008.
  6. E.D. Bloom (1969)، "High-Energy Inelastic e–p Scattering at 6° and 10°"، Physical Review Letters، 23 (16): 930–934، doi:10.1103/PhysRevLett.23.930.
  7. M. Breidenbach (1969)، "Observed Behavior of Highly Inelastic Electron–Proton Scattering"، Physical Review Letters، 23 (16): 935–939، doi:10.1103/PhysRevLett.23.935.
  8. M. Gell-Mann (1964)، "A Schematic Model of Baryons and Mesons"، Physics Letters، 8 (3): 214–215، doi:10.1016/S0031-9163(64)92001-3.
  9. G. Zweig (1964)، "An SU(3) Model for Strong Interaction Symmetry and its Breaking"، CERN Report No.8181/Th 8419.
  10. G. Zweig (1964)، "An SU(3) Model for Strong Interaction Symmetry and its Breaking: II"، CERN Report No.8419/Th 8412.
  11. M. Gell-Mann (2000) [1964]، "The Eightfold Way: A theory of strong interaction symmetry"، في M. Gell-Manm, Y. Ne'emann (المحرر)، The Eightfold Way، تايلور وفرانسيس، ص. 11، ISBN 0-7382-0299-1.
    Original: M. Gell-Mann (1961)، "The Eightfold Way: A theory of strong interaction symmetry"، Synchroton Laboratory Report CTSL-20، معهد كاليفورنيا للتقنية،
  12. Y. Ne'emann (2000) [1964]، "Derivation of strong interactions from gauge invariance"، في M. Gell-Manm, Y. Ne'emann (المحرر)، The Eightfold Way، تايلور وفرانسيس، ISBN 0-7382-0299-1.
    Original Y. Ne'emann (1961)، "Derivation of strong interactions from gauge invariance"، Nuclear Physics، 26: 222، doi:10.1016/0029-5582(61)90134-1.
  13. Companion to the History of Modern Science، تايلور وفرانسيس، 1996، ص. 673، ISBN 0415145783. {{استشهاد بكتاب}}: الوسيط |الأول= يفتقد |الأول= (مساعدة)
  14. A. Pickering (1984)، Constructing Quarks، دار نشر جامعة شيكاغو، ص. 114–125، ISBN 0226667995.
  15. B.J. Bjorken, S.L. Glashow (1964)، "Elementary Particles and SU(4)"، Physics Letters، 11 (3): 255–257، doi:10.1016/0031-9163(64)90433-0.
  16. J.I. Friedman، "The Road to the Nobel Prize"، Hue University، مؤرشف من الأصل في 23 يونيو 2016، اطلع عليه بتاريخ 29 سبتمبر 2008.
  17. R.P. Feynman (1969)، "Very High-Energy Collisions of Hadrons"، Physical Review Letters، 23 (24): 1415–1417، doi:10.1103/PhysRevLett.23.1415.
  18. S. Kretzer؛ وآخرون (2004)، "CTEQ6 Parton Distributions with Heavy Quark Mass Effects"، فيزيكال ريفيو، 69 (11): 114005، doi:10.1103/PhysRevD.69.114005، أرشيف خي:0307022v1}}. {{استشهاد بدورية محكمة}}: Explicit use of et al. in: |مؤلف= (مساعدة)
  19. D.J. Griffiths (1987)، Introduction to Elementary Particles، جون وايلي وأولاده ‏، ص. 42، ISBN 0-471-60386-4.{{استشهاد بكتاب}}: صيانة CS1: extra punctuation (link)
  20. M.E. Peskin, D.V. Schroeder (1995)، An introduction to quantum field theory، أديسون-ويسلي ‏، ص. 556، ISBN 0-201-50397-2.{{استشهاد بكتاب}}: صيانة CS1: extra punctuation (link)
  21. V.V. Ezhela (1996)، Particle physics، سبرنجر، ص. 2، ISBN 1563966425.
  22. S.L. Glashow, J. Iliopoulos, L. Maiani (1970)، "Weak Interactions with Lepton–Hadron Symmetry"، فيزيكال ريفيو، 2 (7): 1285–1292، doi:10.1103/PhysRevD.2.1285.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
  23. D.J. Griffiths (1987)، Introduction to Elementary Particles، جون وايلي وأولاده ‏، ص. 44، ISBN 0-471-60386-4.{{استشهاد بكتاب}}: صيانة CS1: extra punctuation (link)
  24. M. Kobayashi, T. Maskawa (1973)، "CP-Violation in the Renormalizable Theory of Weak Interaction"، Progress of Theoretical Physics، 49 (2): 652–657، doi:10.1143/PTP.49.652، مؤرشف من الأصل في 13 أكتوبر 2019.
  25. M. Bartusiak (1994)، A Positron named Priscilla، دار نشر الأكاديميات الوطنية، ص. 245، ISBN 0309048931، مؤرشف من الأصل في 7 أبريل 2022.
  26. K.W. Staley (2004)، The Evidence for the Top Quark، مطبعة جامعة كامبريدج، ص. 144، ISBN 0521827108.
  27. "New Precision Measurement of Top Quark Mass"، مختبر بروكهافن الوطني، مؤرشف من الأصل في 8 مايو 2012، اطلع عليه بتاريخ 24 سبتمبر 2008.
  28. J. Gribbin, M. Gribbin (1997)، Richard Feynman: A Life in Science، دار بنجوين للنشر، ص. 194، ISBN 0-452-27631-4.
  29. J. Joyce (1982) [1939]، Finnegans Wake، دار بنجوين للنشر، ص. 383، ISBN 0-14-00-6286-6، LCCN 59-354.
  30. M. Gell-Mann (1995)، The Quark and the Jaguar: Adventures in the Simple and the Complex، هنري هولت وشركاه، ص. 180، ISBN 978-0805072532.
  31. J. Gleick (1992)، Genius: Richard Feynman and modern physics، Little Brown and Company، ص. 390، ISBN 0-316-903167.
  32. J.J. Sakurai (1994)، S.F Tuan (المحرر)، Modern Quantum Mechanics (ط. Revised)، أديسون-ويسلي ‏، ص. 376، ISBN 0-201-53929-2.{{استشهاد بكتاب}}: صيانة CS1: extra punctuation (link)
  33. D.H. Perkins (2000)، Introduction to high energy physics، مطبعة جامعة كامبريدج، ص. 8، ISBN 0521621968.
  34. M. Riordan (1987)، The Hunting of the Quark: A True Story of Modern Physics، سايمون وشوستر، ص. 210، ISBN 9780671504663.
  35. F. Close (2006)، The New Cosmic Onion، سي آر سي بريس، ص. 133، ISBN 1584887982.
  36. C. Amsler et al. (Particle Data Group) (2008)، "Higgs Bosons: Theory and Searches" (PDF)، Physics Letters B، 667 (1): 1–1340، doi:10.1016/j.physletb.2008.07.018، مؤرشف من الأصل (PDF) في 1 فبراير 2017.
  37. S.S.M. Wong (1998)، Introductory Nuclear Physics (ط. 2nd)، جون وايلي وأولاده ‏، ص. 30، ISBN 0-471-23973-9.{{استشهاد بكتاب}}: صيانة CS1: extra punctuation (link)
  38. K.A. Peacock (2008)، The Quantum Revolution، Greenwood Publishing Group، ص. 125، ISBN 031333448X.
  39. B. Povh, C. Scholz, K. Rith, F. Zetsche (2008)، Particles and Nuclei، سبرنجر، ص. 98، ISBN 3540793674.{{استشهاد بكتاب}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
  40. Section 6.1. in P.C.W. Davies (1979)، The Forces of Nature، مطبعة جامعة كامبريدج، ISBN 052122523X.
  41. M. Munowitz (2005)، Knowing، مطبعة جامعة أكسفورد، ص. 35، ISBN 0195167376.
  42. W.-M. Yao et al. (Particle Data Group) (2006)، "Review of Particle Physics: Pentaquark Update" (PDF)، Journal of Physics G، 33 (1): 1–1232، doi:10.1088/0954-3899/33/1/001، مؤرشف من الأصل (PDF) في 21 ديسمبر 2018.
  43. C. Amsler et al. (Particle Data Group) (2008)، "Review of Particle Physics: Pentaquarks" (PDF)، Physics Letters B، 667 (1): 1–1340، doi:10.1016/j.physletb.2008.07.018، مؤرشف من الأصل (PDF) في 21 ديسمبر 2018.
    C. Amsler et al. (Particle Data Group) (2008)، "Review of Particle Physics: New Charmonium-Like States" (PDF)، Physics Letters B، 667 (1): 1–1340، doi:10.1016/j.physletb.2008.07.018، مؤرشف من الأصل (PDF) في 21 ديسمبر 2018.
    E.V. Shuryak (2004)، The QCD Vacuum, Hadrons and Superdense Matter، World Scientific، ص. 59، ISBN 9812385746. {{استشهاد بكتاب}}: الوسيط |archive-url= بحاجة لـ |url= (مساعدة)
  44. C. Amsler et al. (Particle Data Group) (2008)، "Review of Particle Physics: b′ (4th Generation) Quarks, Searches for" (PDF)، Physics Letters B، 667 (1): 1–1340، doi:10.1016/j.physletb.2008.07.018، مؤرشف من الأصل (PDF) في 21 ديسمبر 2018.
    C. Amsler et al. (Particle Data Group) (2008)، "Review of Particle Physics: t′ (4th Generation) Quarks, Searches for" (PDF)، Physics Letters B، 667 (1): 1–1340، doi:10.1016/j.physletb.2008.07.018، مؤرشف من الأصل (PDF) في 21 ديسمبر 2018.
  45. D. Decamp (1989)، "Determination of the number of light neutrino species"، Physics Letters B، 231 (4): 519، doi:10.1016/0370-2693(89)90704-1.
    A. Fisher (1991)، "Searching for the Beginning of Time: Cosmic Connection"، بوبيولار ساينس، 238 (4): 70، مؤرشف من الأصل في 14 أغسطس 2014.
    J.D. Barrow (1997) [1994]، "The Singularity and Other Problems"، The Origin of the Universe (ط. Reprint)، بيزيك بوكس ‏، ISBN 978-0465053148. {{استشهاد بكتاب}}: الوسيط |archive-url= بحاجة لـ |url= (مساعدة)صيانة CS1: extra punctuation (link)
  46. D.H. Perkins (2003)، Particle Astrophysics، مطبعة جامعة أكسفورد، ص. 4، ISBN 0198509529.
  47. G. Fraser (2006)، The New Physics for the Twenty-First Century، مطبعة جامعة كامبريدج، ص. 91، ISBN 0521816009، مؤرشف من الأصل في 23 أكتوبر 2021.
  48. "The Standard Model of Particle Physics"، بي بي سي، 2002، مؤرشف من الأصل في 21 يناير 2011، اطلع عليه بتاريخ 19 أبريل 2009.
  49. F. Close (2006)، The New Cosmic Onion، سي آر سي بريس، ص. 80–90، ISBN 1584887982.
  50. D. Lincoln (2004)، Understanding the Universe، World Scientific، ص. 116، ISBN 9812387056.
  51. "Weak Interactions"، Virtual Visitor Center، مركز المعجل الخطي ستانفورد، 2008، مؤرشف من الأصل في 23 نوفمبر 2011، اطلع عليه بتاريخ 28 سبتمبر 2008.
  52. C. Amsler؛ وآخرون (2008)، "Review of Particles Physics: The CKM Quark-Mixing Matrix" (PDF)، Physics Letters، B667 (1): 1–1340، مؤرشف من الأصل (PDF) في 21 ديسمبر 2018. {{استشهاد بدورية محكمة}}: Explicit use of et al. in: |مؤلف= (مساعدة)
  53. Z. Maki, M. Nakagawa, S. Sakata (1962)، "Remarks on the Unified Model of Elementary Particles"، Progress of Theoretical Physics، 28 (5): 870، doi:10.1143/PTP.28.870، مؤرشف من الأصل في 21 أبريل 2019.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
  54. B.C. Chauhan, M. Picariello, J. Pulido, E. Torrente-Lujan (2007)، "Quark–lepton complementarity, neutrino and standard model data predict
    θPMNS
    13     = 9°+1°
    −2°    "، European Physical Journal، C50 (3): 573–578، doi:10.1140/epjc/s10052-007-0212-z، أرشيف خي:hep-ph/0605032}}.    {{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
  55. R. Nave، "The Color Force"، هايبرفيزيكس، جامعة ولاية جورجيا, Department of Physics and Astronomy، مؤرشف من الأصل في 7 أكتوبر 2018، اطلع عليه بتاريخ 26 أبريل 2009.
  56. B.A. Schumm (2004)، Deep Down Things، مطبعة جامعة جونز هوبكينز، ص. 131–132، ISBN 080187971X، OCLC 55229065.
  57. Part III of M.E. Peskin, D.V. Schroeder (1995)، An Introduction to Quantum Field Theory، أديسون-ويسلي ‏، ISBN 0-201-50397-2، مؤرشف من الأصل في 14 أغسطس 2021.{{استشهاد بكتاب}}: صيانة CS1: extra punctuation (link)
  58. V. Icke (1995)، The force of symmetry، مطبعة جامعة كامبريدج، ص. 216، ISBN 052145591X، مؤرشف من الأصل في 17 فبراير 2022.
  59. M.Y. Han (2004)، A story of light، World Scientific، ص. 78، ISBN 9812560343.
  60. C. Sutton، "Quantum chromodynamics (physics)"، موسوعة بريتانيكا، مؤرشف من الأصل في 9 ديسمبر 2010، اطلع عليه بتاريخ 12 مايو 2009.
  61. A. Watson (2004)، The Quantum Quark، مطبعة جامعة كامبريدج، ص. 285–286، ISBN 0521829070.
  62. C. Amsler et al. (Particle Data Group) (2008)، "Review of Particle Physics: Quarks" (PDF)، Physics Letters B، 667 (1): 1–1340، doi:10.1016/j.physletb.2008.07.018، مؤرشف من الأصل (PDF) في 21 ديسمبر 2018.
  63. W. Weise, A.M. Green (1984)، Quarks and Nuclei، World Scientific، ص. 65–66، ISBN 9971966611.
  64. D. McMahon (2008)، Quantum Field Theory Demystified، مكغرو هيل، ص. 17، ISBN 0071543821.
  65. S.G. Roth (2007)، Precision electroweak physics at electron–positron colliders، سبرنجر، ص. VI، ISBN 3540351647.
  66. R.P. Feynman (1985)، QED: The Strange Theory of Light and Matter (ط. 1st)، دار نشر جامعة برنستون، ص. 136–137، ISBN 0-691-08388-6.
  67. M. Veltman (2003)، Facts and Mysteries in Elementary Particle Physics، World Scientific، ص. 45–47، ISBN 981238149X.
  68. F. Wilczek, B. Devine (2006)، Fantastic Realities، World Scientific، ص. 85، ISBN 981256649X، مؤرشف من الأصل في 18 مارس 2022.
  69. F. Wilczek, B. Devine (2006)، Fantastic Realities، World Scientific، ص. 400ff، ISBN 981256649X.
  70. M. Veltman (2003)، Facts and Mysteries in Elementary Particle Physics، World Scientific، ص. 295–297، ISBN 981238149X.
  71. T. Yulsman (2002)، Origin، سي آر سي بريس، ص. 55، ISBN 075030765X.
  72. F. Garberson (2008)، "Top Quark Mass and Cross Section Results from the Tevatron"، arXiv:0808.0273 [hep-ex].
  73. J. Steinberger (2005)، Learning about Particles، سبرنجر، ص. 130، ISBN 3540213295.
  74. C.-Y. Wong (1994)، Introduction to High-energy Heavy-ion Collisions، World Scientific، ص. 149، ISBN 9810202636.
  75. S.B. Rüester, V. Werth, M. Buballa, I.A. Shovkovy, D.H. Rischke (2005)، "The phase diagram of neutral quark matter: Self-consistent treatment of quark masses"، فيزيكال ريفيو، 72: 034003، doi:10.1103/PhysRevD.72.034004، أرشيف خي:hep-ph/0503184}}.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
  76. M.G. Alford, K. Rajagopal, T. Schaefer, A. Schmitt (2008)، "Color superconductivity in dense quark matter"، Reviews of Modern Physics، 80: 1455–1515، doi:10.1103/RevModPhys.80.1455، أرشيف خي:0709.4635}}.{{استشهاد بدورية محكمة}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)
  77. S. Mrowczynski (1998)، "Quark–Gluon Plasma"، Acta Physica Polonica B، 29: 3711، أرشيف خي:nucl-th/9905005}}، مؤرشف من الأصل (PDF) في 04 أغسطس 2009.
  78. Z. Fodor, S.D. Katz (2004)، "Critical point of QCD at finite T and μ, lattice results for physical quark masses"، Journal of High Energy Physics، 2004: 50، doi:10.1088/1126-6708/2004/04/050، أرشيف خي:hep-lat/0402006}}.
  79. U. Heinz, M. Jacob (2000)، "Evidence for a New State of Matter: An Assessment of the Results from the CERN Lead Beam Programme"، arXiv:nucl-th/0002042. {{استشهاد بأرخايف}}: الوسيط |class= تم تجاهله (مساعدة)
  80. "RHIC Scientists Serve Up "Perfect" Liquid"، مختبر بروكهافن الوطني، 2005، مؤرشف من الأصل في 16 يوليو 2012، اطلع عليه بتاريخ 22 مايو 2009.
  81. T. Yulsman (2002)، Origins: The Quest for Our Cosmic Roots، سي آر سي بريس، ص. 75، ISBN 075030765X.
  82. A. Sedrakian, J.W. Clark, M.G. Alford (2007)، Pairing in fermionic systems، World Scientific، ص. 2–3، ISBN 9812569073، مؤرشف من الأصل في 8 أبريل 2022.{{استشهاد بكتاب}}: صيانة CS1: أسماء متعددة: قائمة المؤلفون (link)

قراءات أخرى

وصلات خارجية
  • بوابة الفيزياء

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.