How to Graph Polar Equations

Learn to plot and graph polar equations using radians, angles, and tables

Last Updated: February 28, 2023 References

Polar functions are functions of the form r = f(θ). While you can make some really cool graphs with them, they are really quite tricky to work with.^{[1]
X
Research source}

Steps

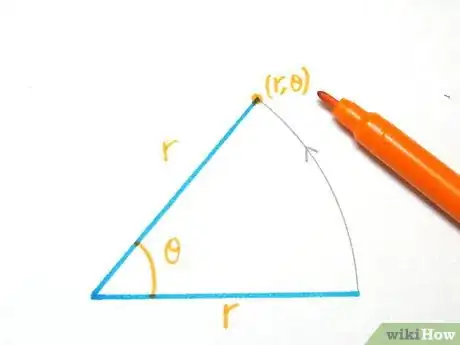
1
Understand how polar equations work. Coordinates in polar equations are of the form (r,θ), where r represents radius and θ represents angle. This means you rotate θ radians around and go out r units.^{[2]
X
Research source}
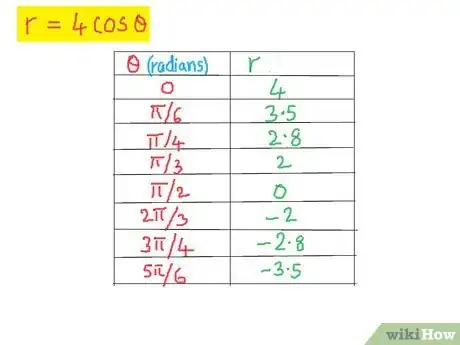
2
Make a table with values of the angle and radius. Take any random values of θ (around ten values would suffice) and calculate r against each of them using the relationship given between r and θ. This will help you plot them out on a graph easier, because you can just refer to a table instead of having to come up with coordinates in your head.^{[3]
X
Research source}

Advertisement
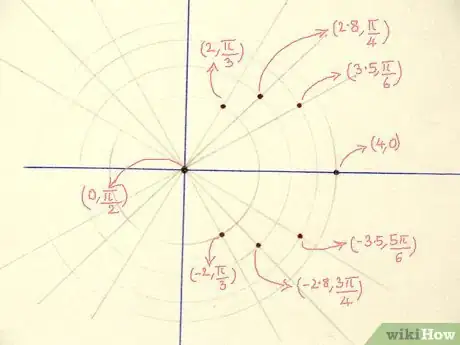
3
Plot the various (r,θ) points as found in the table.^{[4]
X
Research source}
The wikiHow How to Plot Polar Coordinates will be helpful.
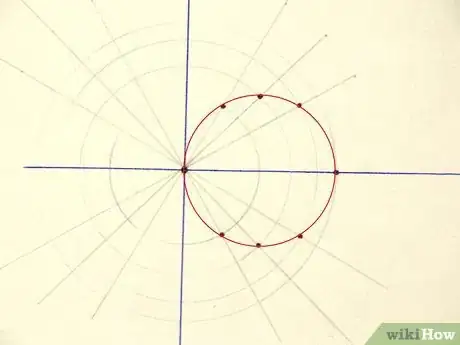
4
Join the plotted points with a smooth curve and you're done!^{[5]
X
Research source}

Community Q&A

Question

How do I graph r = 2 + 3cos theta?

Community Answer

Make a theta and r table. Plug in various values of theta. Lastly, graph on polar graph paper.
Question

How do I graph 1 - 3 sin theta?

Donagan

Top Answerer

Let one of the axes (say, the x-axis) show the values of theta (Θ) from 0° to 90° (or higher). Let the other axis (y) show the values of the function (1 - 3 sin Θ). Construct a table of values pairing each theta value with its respective function value. Then plot the graph as you would with x and y values. You'll need a trig table for the sine values.

Warnings

If you graph this by hand, making θ's interval too large will result in an inaccurate graph. Try to choose an interval that won't be too inaccurate but won't be too time consuming to graph.

⧼thumbs_response⧽
Helpful 0 Not Helpful 0