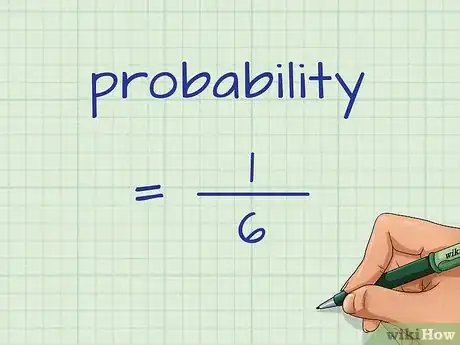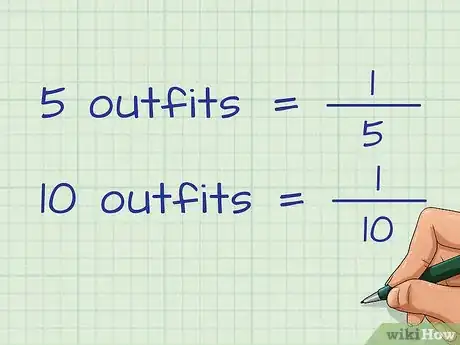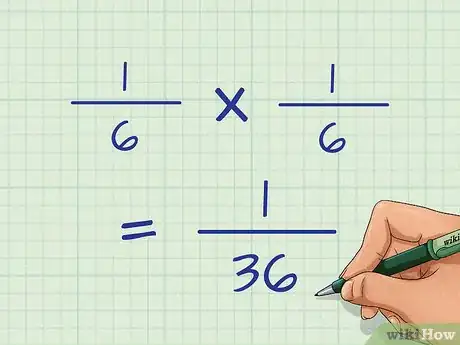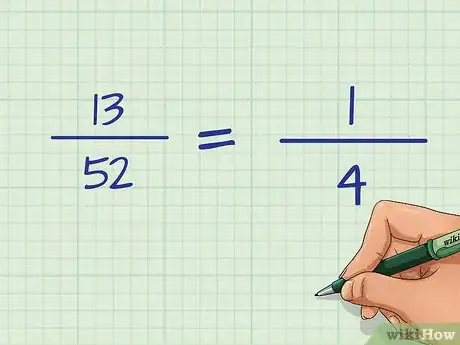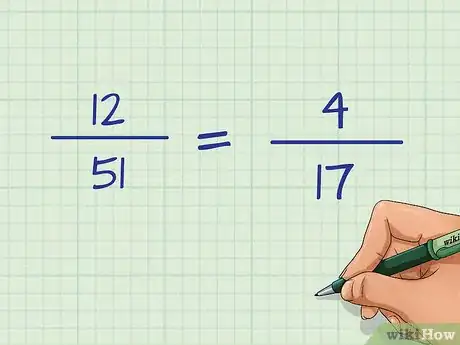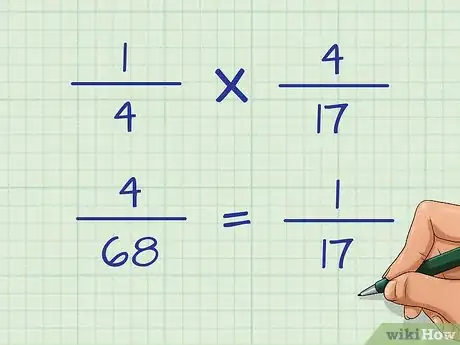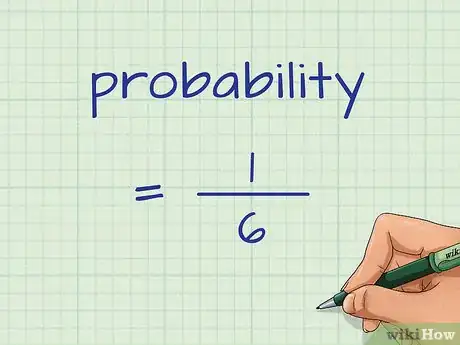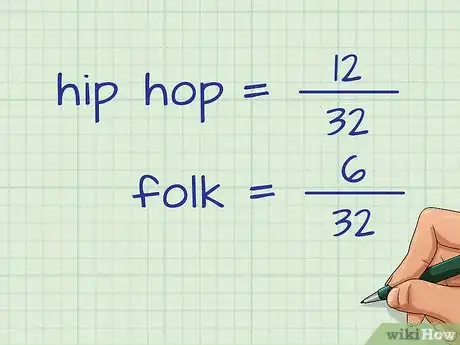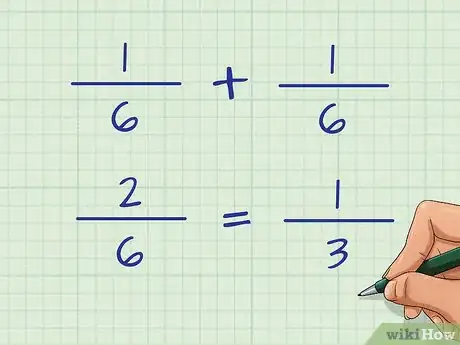Cómo aprender sobre las probabilidades

Saber cómo calcular la probabilidad de que ocurra un acontecimiento puede ser una habilidad valiosa cuando tomas decisiones, sin importar si se trata de un juego o una situación de la vida real. Sin embargo, la manera en la que calcules las probabilidades cambiará según el tipo de acontecimiento que planeas que ocurrirá. Por ejemplo, no calcularás tus probabilidades de ganarte la lotería de la misma forma que calcularías las probabilidades de conseguir un full house en una partida de póker. Luego de determinar si los acontecimientos son independientes, condicionales o mutuamente exclusivos, calcular su probabilidad será muy simple.

Parte 1

Parte 1 de 4:
Entender el significado de probabilidad

1
Reflexiona sobre la definición de probabilidad. Esta consiste en la posibilidad de que un acontecimiento aleatorio ocurra.^{[1]
X
Fuente de investigación} Suele expresarse como una proporción.
- Dado que la probabilidad se expresa como proporción o fracción, puedes considerarla como la posibilidad de que algo ocurra en una escala de 0 a 1, en la que 0 es ninguna probabilidad, y 1 es una certeza total (es decir, el acontecimiento ocurrirá en la proporción 1/1).^{[2]
  X
  Fuente de investigación}
- La probabilidad describe acontecimientos aleatorios. Estos son acontecimientos que no pueden predecirse,^{[3]
  X
  Fuente de investigación} como tomar una carta determinada de una baraja o recibir el impacto de un rayo.
2
Aprende la fórmula para determinar la probabilidad. La probabilidad de que algo ocurra se define con la proporción $probabilidad={\frac {nro.\;de\;resultados\;favorables}{nro.\;de\;posibles\;resultados}}$ , en donde un resultado favorable es el acontecimiento que buscas que ocurra.^{[4]
X
Fuente de investigación}
3
Determina la probabilidad de que ocurra un acontecimiento determinado. Para ello, completa la proporción de probabilidades determinando cuántos resultados favorables puedes tener, y cuántos posibles resultados puedes conseguir.^{[5]
X
Fuente de especialista

Mario Banuelos, PhD
Profesor asistente de matemáticas
Entrevista a especialista. 11 de diciembre de 2020.}
- Para entender la teoría de probabilidad más compleja, primero debes entender cómo determinar la probabilidad de que ocurra un acontecimiento aleatorio determinado, y lo que esta significa.
- Por ejemplo, si tienes un frasco con 10 canicas rojas y 5 azules, quizás quieras saber cuál es la probabilidad de tomar una azul de forma aleatoria. Dado que tienes 5 azules, la cantidad de resultados favorables será 5. Tienes un total de 15 canicas en el frasco, por lo que el número de posibles resultados es 15. La proporción de probabilidad será así:
  $probabilidad={\frac {nro.\;de\;resultados\;favorables}{nro.\;de\;posibles\;resultados}}$
  $probabilidad={\frac {5}{15}}$
  $probabilidad\;simplificada={\frac {1}{3}}$ . Por lo tanto, la probabilidad de tomar una canica azul al azar es de 1 de 3.

Parte 2

Parte 2 de 4:
Identificar la probabilidad de tener varios acontecimientos independientes

1
Determina si los dos acontecimientos son independientes. Los acontecimientos independientes son aquellos en los que el resultado de uno no afectará la probabilidad de que el otro ocurra.^{[6]
X
Fuente de investigación}
- Por ejemplo, si vas a usar dos dados, quizás quieras saber cuál es la probabilidad de que consigas dos 3. La probabilidad de que consigas un 3 con un dado no afectará la posibilidad de que consigas este número con el segundo dado. Por lo tanto, los acontecimientos son independientes.
2
Identifica la probabilidad del primer acontecimiento. Para ello, establece la proporción $probabilidad={\frac {nro.\;de\;resultados\;favorables}{nro.\;de\;posibles\;resultados}}$ $probabilidad={\frac {nro.\;de\;resultados\;favorables}{nro.\;de\;posibles\;resultados}}$ , en donde un resultado favorable es el acontecimiento que deseas que ocurra.
- Por ejemplo, si el primero es conseguir un 3 con un dado, la cantidad de resultados favorables será 1, ya que solo hay un 3 en el dado. La cantidad de posibles resultados es 6, ya que el dado tiene seis lados. Por lo tanto, la proporción lucirá así: $probabilidad={\frac {1}{6}}$ .
3
Halla la probabilidad del segundo acontecimiento. Para ello, establece la proporción, tal como lo has hecho para el primer acontecimiento.
- Por ejemplo, si el segundo acontecimiento también es conseguir un 3 con un dado, la probabilidad será la misma que la del primero: $probabilidad={\frac {1}{6}}$ .
- La probabilidad podría variar en el primer y el segundo acontecimiento. Por ejemplo, si una compañera de clase y tú tienen el mismo atuendo, podrías querer saber la probabilidad de que lo usen en la escuela el mismo día. Si tienes 5 atuendos, las probabilidades de que lo uses será de ${\frac {1}{5}}$ ; pero si tu compañera tiene 10 atuendos, la probabilidad de que ella lo use será de ${\frac {1}{10}}$ .
4
Multiplica las probabilidades de acontecimientos individuales. Esto te dará la probabilidad de que ambos ocurran.^{[7]
X
Fuente de investigación}
- Lee este artículo para repasar sobre la multiplicación de fracciones.
- Por ejemplo, si la probabilidad de conseguir un 3 con un dado es ${\frac {1}{6}}$ , y la de conseguir otro 3 con el segundo dado también es ${\frac {1}{6}}$ , identificarás la probabilidad de que ambos acontecimientos ocurran con este cálculo ${\frac {1}{6}}\times {\frac {1}{6}}={\frac {1}{36}}$ . Por lo tanto, la probabilidad de conseguir dos 3 es 1 de 36.

Parte 3

Parte 3 de 4:
Identificar la probabilidad de tener acontecimientos condicionales

1
Determina si los dos acontecimientos son condicionales. Un acontecimiento condicional (también llamado dependiente) es aquel que puede verse afectado por los que ocurran antes que él.^{[8]
X
Fuente de investigación}
- Por ejemplo, si estás robando cartas de una baraja común, quizás quieras determinar la probabilidad de conseguir una carta de corazones cuando robes por primera y segunda vez. Tomar una carta de corazones la primera vez afectará la probabilidad de que esto vuelva a ocurrir, ya que habrá una cantidad menor de estas cartas (y cartas en general) en la baraja una vez que robes la primera.
2
Identifica la probabilidad de que ocurra el primer acontecimiento. Para ello, establece la proporción $probabilidad={\frac {nro.\;de\;resultados\;favorables}{nro.\;de\;posibles\;resultados}}$ $probabilidad={\frac {nro.\;de\;resultados\;favorables}{nro.\;de\;posibles\;resultados}}$ , en donde un resultado favorable será el acontecimiento que deseas que ocurra.
- Por ejemplo, si el primer acontecimiento es robar una carta de corazones de la baraja, el número de resultados favorables será 13, ya que hay 13 de estas cartas en una baraja. La cantidad de posibles resultados es 52, ya que una baraja tiene 52 cartas en total. Por lo tanto, la proporción lucirá así: $probabilidad={\frac {13}{52}}$ . En pocas palabras, la probabilidad será de ${\frac {1}{4}}$ .
3
Determina la probabilidad de que ocurra el segundo acontecimiento, teniendo en cuenta que el primero ya ha ocurrido.^{[9]
X
Fuente de investigación} Para ello, tendrás que evaluar la manera en la que el primero afectará la cantidad de resultados posibles y favorables del segundo.
- Por ejemplo, si has robado una carta de corazones la primera vez, ahora solo quedarán 12 en la baraja, y solo 51 cartas en total. Por lo tanto, la probabilidad de robar otra la segunda vez es de ${\frac {12}{51}}$ . En pocas palabras, la probabilidad es de ${\frac {4}{17}}$ .
4
Multiplica las probabilidades de los acontecimientos individuales. Esto te dará la probabilidad de que ambos acontecimientos ocurran.^{[10]
X
Fuente de investigación}
- Lee este artículo para repasar sobre la multiplicación de fracciones.
- Si la probabilidad de robar una carta de corazones la primera vez es de ${\frac {1}{4}}$ , y la de robar otra la segunda vez (teniendo en cuenta que ya has tomado una) es de ${\frac {4}{17}}$ , podrás identificar la probabilidad de que ambos acontecimientos ocurran con el siguiente cálculo:
  ${\frac {1}{4}}\times {\frac {4}{17}}={\frac {4}{68}}$
  ${\frac {4}{68}}={\frac {1}{17}}$
  Por lo tanto, la probabilidad de robar cartas de corazones la primera y segunda vez será de 1 de 17.

Parte 4

Parte 4 de 4:
Determinar la probabilidad de tener acontecimientos mutuamente exclusivos

1
Determina si los dos acontecimientos son mutuamente exclusivos. Estos son acontecimientos que no pueden ocurrir al mismo tiempo.^{[11]
X
Fuente de investigación}
- Estos se marcan con la conjunción o, mientras que los acontecimientos que no son mutuamente exclusivos usarán la conjunción y.^{[12]
  X
  Fuente de investigación}
- Por ejemplo, si vas a lanzar un dado, quizás quieras conocer la probabilidad de conseguir un 3 o un 4. No puedes conseguir un 3 y un 4 con un solo dado, por lo que estos acontecimientos son mutuamente exclusivos.
2
Identifica la probabilidad de que ocurra el primer acontecimiento. Para ello, establece la proporción $probabilidad={\frac {nro.\;de\;resultados\;favorables}{nro.\;de\;posibles\;resultados}}$ $probabilidad={\frac {nro.\;de\;resultados\;favorables}{nro.\;de\;posibles\;resultados}}$ , en donde un resultado favorable sea el acontecimiento que deseas que ocurra.
- Por ejemplo, si el primer acontecimiento es conseguir un 3 con un dado, la cantidad de resultados favorables será 1, ya que solo hay un 3 en el dado. La cantidad de posibles resultados es 6, ya que los dados tienen seis lados. Por lo tanto, la proporción lucirá así: $probabilidad={\frac {1}{6}}$ .
3
Halla la probabilidad del segundo acontecimiento. Para ello, establece la proporción, tal como lo has hecho con el primer acontecimiento.
- Si el segundo acontecimiento es conseguir un 4 con un dado, la probabilidad será la misma que la del primero: $probabilidad={\frac {1}{6}}$ .
- La probabilidad podría variar en el primer y el segundo acontecimiento. Por ejemplo, quizás quieras hallar la probabilidad de que la siguiente canción aleatoria en una lista de reproducción de 32 canciones sea de hip hop o folk. Si hay 12 canciones de hip hop y 6 de folk en la lista, la probabilidad de que la siguiente sea de hip hop será de ${\frac {12}{32}}$ ; y de que sea de folk, de ${\frac {6}{32}}$ .
4
Suma las probabilidades de los acontecimientos individuales. Esto te dará la probabilidad de que alguno ocurra.
- Lee este artículo para repasar sobre la suma de fracciones.
- Por ejemplo, si la probabilidad de conseguir un 3 con un dado es de ${\frac {1}{6}}$ , y la de conseguir un 4 con un dado también es de ${\frac {1}{6}}$ , podrás hallar la probabilidad de que ambos acontecimientos ocurran con el siguiente cálculo:
  ${\frac {1}{6}}+{\frac {1}{6}}={\frac {2}{6}}$
  ${\frac {2}{6}}={\frac {1}{3}}$
  Por lo tanto, la probabilidad de conseguir un 3 o 4 será de 1 de 3.

[1]

[2]

[3]

[4]

[5]

Fuente de especialista

Mario Banuelos, PhD
Profesor asistente de matemáticas

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Cómo aprender sobre las probabilidades

Pasos

Parte 1

Parte 1 de 4:
Entender el significado de probabilidad

Parte 2

Parte 2 de 4:
Identificar la probabilidad de tener varios acontecimientos independientes

Parte 3

Parte 3 de 4:
Identificar la probabilidad de tener acontecimientos condicionales

Parte 4

Parte 4 de 4:
Determinar la probabilidad de tener acontecimientos mutuamente exclusivos

wikiHows relacionados

Referencias

Acerca de este wikiHow

wikiHows relacionados

¡Suscríbete al boletín gratuito de wikiHow!

Cómo aprender sobre las probabilidades

Pasos

Parte 1 Parte 1 de 4:Entender el significado de probabilidad

Parte 2 Parte 2 de 4:Identificar la probabilidad de tener varios acontecimientos independientes

Parte 3 Parte 3 de 4:Identificar la probabilidad de tener acontecimientos condicionales

Parte 4 Parte 4 de 4:Determinar la probabilidad de tener acontecimientos mutuamente exclusivos

wikiHows relacionados

Referencias

Acerca de este wikiHow

wikiHows relacionados

¡Suscríbete al boletín gratuito de wikiHow!

Parte 1

Parte 1 de 4:
Entender el significado de probabilidad

Parte 2

Parte 2 de 4:
Identificar la probabilidad de tener varios acontecimientos independientes

Parte 3

Parte 3 de 4:
Identificar la probabilidad de tener acontecimientos condicionales

Parte 4

Parte 4 de 4:
Determinar la probabilidad de tener acontecimientos mutuamente exclusivos