Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 35 596 veces.
La media armónica es otra forma de calcular la media (o promedio) de un conjunto de números. Es la forma más apropiada cuando el conjunto de números tiene valores atípicos que podrían sesgar el resultado.[1] La mayoría de las personas están familiarizadas con el cálculo de la media aritmética, que consiste en sumar todos los valores y dividirlos entre la cantidad. El cálculo de la media armónica es un poco más complicado. Si vas a trabajar con un conjunto pequeño de números, puedes resolver las operaciones a mano usando una fórmula. De lo contrario, puedes encontrar rápidamente la media armónica usando Microsoft Excel.
Pasos
Método 1
Método 1 de 3:Plantear la fórmula
-
1Plantea la fórmula de la media armónica. La fórmula es la siguiente , donde es la cantidad de valores del conjunto de números y , , son los valores de dicho conjunto.[2]
-
2Determina los valores para los cuales necesitas encontrar la media armónica. Puede ser cualquier conjunto de números.
- Por ejemplo, supón que necesitas encontrar la media armónica para los números 10, 12, 16 y 8.
-
3Reemplaza en la fórmula. Debes reemplazarla por la cantidad de valores del conjunto.
- Por ejemplo, si necesitas encontrar la media armónica de los números 10, 12, 16 y 8, la cantidad de valores es 4. Por lo tanto, el numerador de la fórmula será 4:
- Por ejemplo, si necesitas encontrar la media armónica de los números 10, 12, 16 y 8, la cantidad de valores es 4. Por lo tanto, el numerador de la fórmula será 4:
-
4Reemplaza en la fórmula los valores cuyo promedio quieras calcular. Ahora hay que tomar los recíprocos de cada número y sumarlos en el denominador de la fórmula.[3] Recuerda que para obtener el recíproco de un número, tienes que convertir dicho número en fracción colocando un 1 en el numerador y el número entero en el denominador.
- Por ejemplo, si los valores del conjunto son 10, 12, 16 y 8, debes escribir las fracciones , , , en el denominador:
- Por ejemplo, si los valores del conjunto son 10, 12, 16 y 8, debes escribir las fracciones , , , en el denominador:
Método 2
Método 2 de 3:Calcular la media armónica a mano o con una calculadora
-
1Suma las fracciones en el denominador. Puedes sumarlas a mano o con una calculadora. Si no vas a usar una calculadora, recuerda que hay que encontrar primero un denominador común. Si quieres aprender más acerca de la suma de fracciones, lee este wikiHow.
- Por ejemplo:
- Por ejemplo:
-
2Divide el numerador entre el denominador. Recuerda que dividir entre una fracción es lo mismo que multiplicar por su recíproca.[4]
- Por ejemplo:
- Por ejemplo:
-
3Convierte la fracción a decimal para encontrar la media del conjunto de números. Para convertir una fracción a decimal, divide el numerador entre el denominador.[5]
- Por ejemplo:
Por lo tanto, la media armónica de los números 10, 12, 16 y 8 es 10,79.
- Por ejemplo:
Método 3
Método 3 de 3:Calcular la media armónica en Excel
-
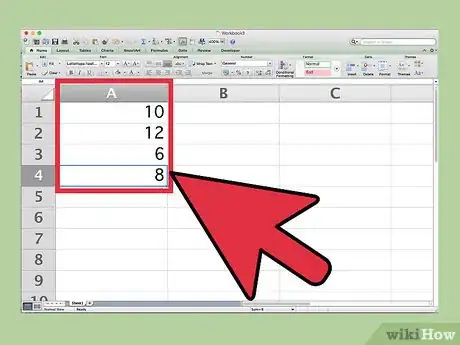
1Ingresa los valores en la hoja de cálculo. Asegúrate de colocar solo un valor en cada celda.
- Por ejemplo, si necesitas encontrar la media armónica de 10, 12, 16 y 8, entonces escribe cada uno de estos valores en una celda separada de la hoja de cálculo. En este caso, en las celdas A1 a A4.
-
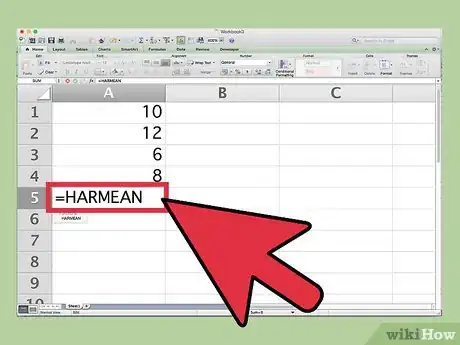
2Ingresa la función de la media armónica. La función es MEDIA.ARMO(número1;[número 2]…).[6] Para seleccionar esta función, empieza a escribir =MEDIA.ARMO en una celda en blanco de la hoja de cálculo y luego haz doble clic en la función cuando esta aparezca.
- Por ejemplo, escribe =MEDIA.ARMO en la celda A5 de la hoja de cálculo y luego haz doble clic en la función.
-
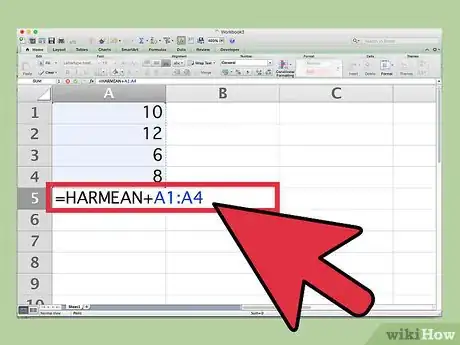
3Selecciona las celdas que contengan los valores cuya media armónica quieras calcular. Presiona la tecla ↵ Enter. Excel ahora calculará la media armónica y la mostrará en la hoja de cálculo.
- Por ejemplo, selecciona las celdas A1 a A4 en tu hoja de cálculo y presiona ↵ Enter. Excel calculará la media armónica, que en este caso es de 10,78652.
Referencias
- ↑ http://economistatlarge.com/finance/applied-finance/differences-arithmetic-geometric-harmonic-means
- ↑ http://www.ck12.org/book/CK-12-Probability-and-Statistics-Concepts/section/5.3/
- ↑ http://www.mathwords.com/h/harmonic_mean.htm
- ↑ https://www.mathsisfun.com/fractions_division.html
- ↑ http://www.purplemath.com/modules/percents2.htm
- ↑ https://support.office.com/en-us/article/HARMEAN-function-5efd9184-fab5-42f9-b1d3-57883a1d3bc6




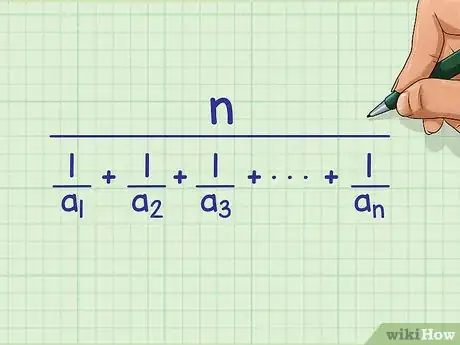





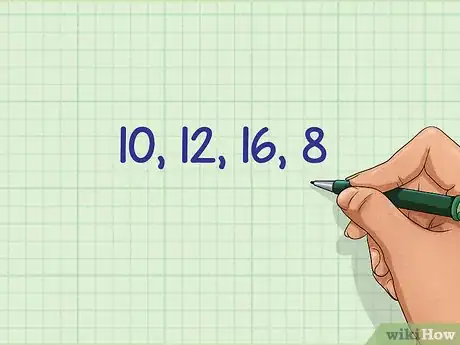


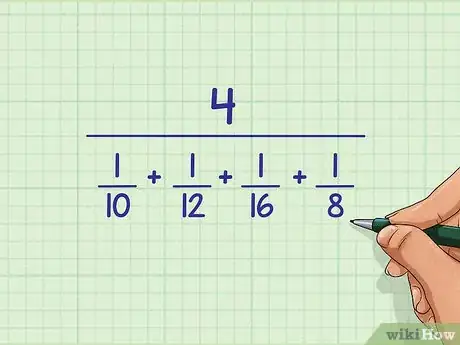





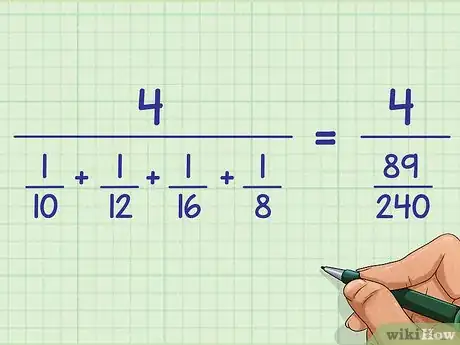

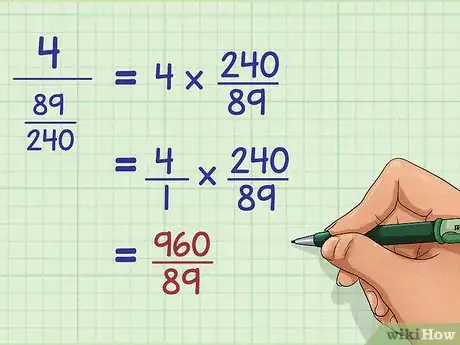



























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 35 596 veces.