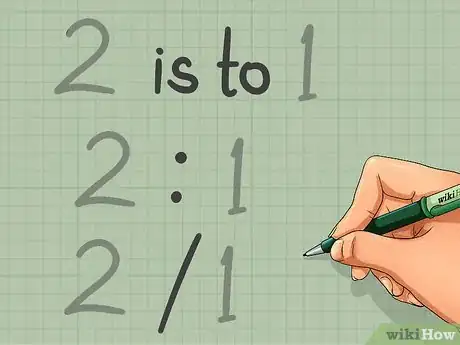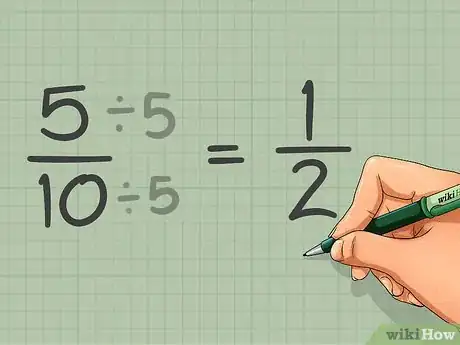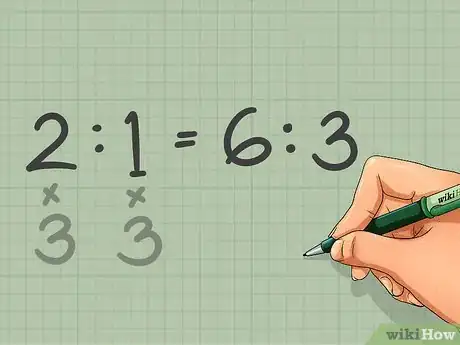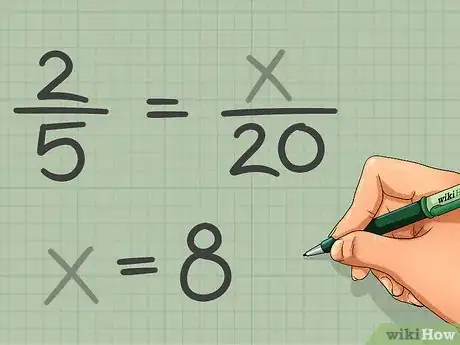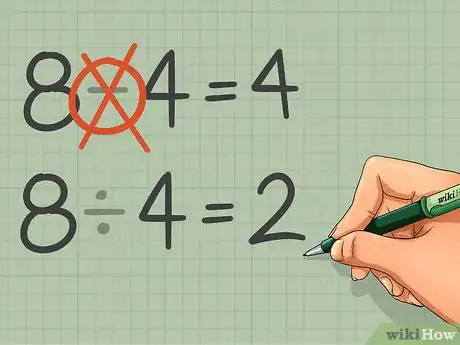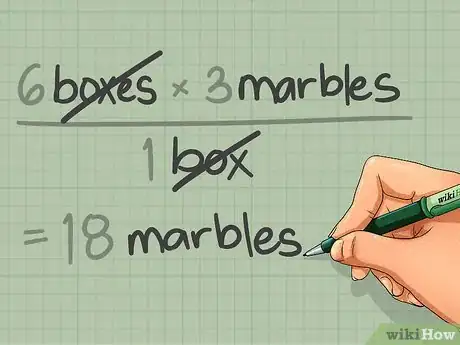Este artículo fue coescrito por Grace Imson, MA. Grace Imson es una maestra de matemáticas con más de 40 años de experiencia docente. Actualmente, Grace es instructora de matemáticas en el City College de San Francisco, y anteriormente trabajó en el Departamento de Matemáticas de la Universidad de Saint Luois. Ha enseñado matemáticas en los niveles de primaria, secundaria, preparatoria y universidad. Tiene una maestría en Educación, con una especialización en Administración y Supervisión de la Universidad de Saint Louis.
Este artículo ha sido visto 321 967 veces.
Las proporciones son expresiones matemáticas que comparan dos o más números. Sirven para comparar cantidades y montos absolutos o también se pueden usar para comparar partes de un todo más grande. Las proporciones se pueden calcular y expresar de varias formas diferentes, pero los principios que regulan su uso son universales a todas ellas.
Pasos
Parte 1
Parte 1 de 3:Entender qué son las proporciones
-
1Aprende cuál es el uso de las proporciones. Las proporciones se usan tanto en entornos académicos como en el mundo real para comparar múltiples montos o cantidades entre sí. Las proporciones más simples comparan solo dos valores, pero también es posible comparar tres o más valores a través de proporciones. En cualquier situación en la cual se comparen dos o más números o cantidades diferentes, es posible aplicar proporciones. Ellas te permiten explicar desde cómo duplicar fórmulas químicas hasta cómo aumentar los ingredientes de una receta de cocina describiendo una cantidad en relación a otra (u otras). Una vez que logres comprenderlas, las utilizarás durante el resto de tu vida.[1]
-
2Aprende qué significa una proporción. Tal como se explicó anteriormente, las proporciones demuestran la cantidad de al menos dos elementos en relación al otro. Así, por ejemplo, si un pastel se prepara con dos tazas de harina y una de azúcar, podrías decir que la proporción de harina con respecto al azúcar es 2 a 1.
- Las proporciones se pueden utilizar para mostrar la relación que existe entre dos cantidades, incluso aunque una no esté directamente vinculada a la otra (como lo estarían en una receta). Por ejemplo, si hay los niños es de 5 a 10. Ninguna cantidad depende de (ni está vinculada a) la otra, sin embargo, cambiaría si alguien se fuera o ingresara un nuevo estudiante. La proporción simplemente compara las cantidades.
-
3Aprende las distintas formas en las que pueden expresarse las proporciones. Las proporciones pueden escribirse usando palabras o representarse a través de símbolos matemáticos.[2]
- Normalmente verás proporciones expresadas a través de palabras (como en los casos anteriores). Debido a que se usan con tanta frecuencia y de tantas formas diferentes, si te encuentras trabajando fuera de los campos de la ciencia o las matemáticas, la forma más común que verás para expresar proporciones, serán las palabras.
- Las proporciones con frecuencia se expresan usando dos puntos (:). Si vas a comparar dos números en una proporción, deberás usar dos puntos (por ejemplo, 7 : 13) y si vas a comparar más de dos números, deberás incluir dos puntos entre cada conjunto de números en forma sucesiva (por ejemplo, 10 : 2 : 23). En el ejemplo de la clase, podríamos comparar el número de niños con el número de niñas usando la proporción 5 niñas : 10 niños. También puedes expresar la proporción simplemente como 5 : 10.
- Las proporciones a menudo también se expresan usando notación fraccional. En el caso de la clase, podrías representar las 5 niñas y los 10 niños simplemente como 5/10. Dicho esto, es necesario aclarar que no debes leerlo igual que a una fracción y debes tener en cuenta que esos números no representan una parte de un todo.
Anuncio
Parte 2
Parte 2 de 3:Utilizar las proporciones
-
1Reduce una proporción a su forma más simple. Las proporciones se pueden reducir y simplificar al igual que las fracciones eliminando los factores comunes de los términos de la proporción. Para reducir una proporción, divide todos sus términos por los factores comunes que compartan hasta que no quede ningún factor común. Sin embargo, cuando lo hagas, es importante no perder de vista las cantidades originales que produjeron esa proporción en primer lugar.[3]
- En el ejemplo anterior de la clase, las 5 niñas sobre 10 niños (5 : 10), ambos lados de la proporción tienen un factor de 5. Divide ambos lados por 5 (el factor común más grande) para obtener 1 niña sobre 2 niños (o 1 : 2). Sin embargo, debes tener presentes las cantidades originales, incluso aunque vayas a usar la proporción reducida. No hay 3 estudiantes en la clase, sino 15. La proporción reducida simplemente compara la relación que existe entre el número de niños y niñas. Existen dos niños por cada niña, y no precisamente 2 niños y 1 niña.
- Algunas proporciones no pueden reducirse. Por ejemplo, 3 : 56 no puede reducirse porque los dos números no comparten un factor común (3 es un número primo y 56 no es divisible por 3).
-
2Utiliza la multiplicación o división para "escalar" proporciones. Un tipo de problema bastante común que use proporciones podría incluir el uso de proporciones para escalar hacia arriba o hacia abajo dos números, uno en relación con el otro. Multiplicar o dividir todos los términos de la proporción por el mismo número crea una proporción con la misma relación que la proporción original, por lo tanto, para escalar una proporción, multiplica o divide la proporción por el factor de escala.[4]
- Por ejemplo: un pastelero necesita triplicar el tamaño de la receta de un pastel. Si la proporción normal de harina con respecto al azúcar es de 2 a 1 (2 : 1), entonces ambos números deben incrementarse en un factor de 3. Las cantidades apropiadas para la receta, ahora son 6 tazas de harina cada 1 de azúcar (6 : 3).
- También puedes hacer el proceso inverso. Si el pastelero necesita solo la mitad de la receta normal, puedes multiplicar ambas cantidades por 1/2 (o dividirlas por dos). El resultado sería 1 taza de harina cada 1/2 taza (0,5 tazas) de azúcar.
-
3Busca variables desconocidas cuando tienes dos proporciones equivalentes. Otro tipo común de problema que incluye el uso de proporciones, es encontrar una variable desconocida en una proporción dado otro número en esa proporción y una segunda proporción que sea equivalente a la primera. Los principios de la regla de tres hacen que resolver estos problemas sea bastante sencillo. Escribe cada proporción en forma de fracción, luego iguala las dos proporciones entre sí y aplica la regla de tres para resolverlo.[5]
- Por ejemplo, supón que tienes un pequeño grupo de estudiantes que incluye 2 niños y 5 niñas. Si quisieras mantener esa proporción de niños y niñas, ¿cuántos niños debería haber en una clase con 20 niñas? Para resolverlo, primero crea las dos proporciones, una con variables desconocidas: 2 niños : 5 niñas = x niños : 20 niñas. Si conviertes estas proporciones a la forma de fracción, obtendrás 2/5 y x/20. Al aplicar la regla de tres, te quedarán 5x = 40 y puedes resolverlo dividiendo ambos términos por 5. La solución final es x = 8.
CONSEJO DE ESPECIALISTAGrace Imson es una maestra de matemáticas con más de 40 años de experiencia docente. Actualmente, Grace es instructora de matemáticas en el City College de San Francisco, y anteriormente trabajó en el Departamento de Matemáticas de la Universidad de Saint Luois. Ha enseñado matemáticas en los niveles de primaria, secundaria, preparatoria y universidad. Tiene una maestría en Educación, con una especialización en Administración y Supervisión de la Universidad de Saint Louis.Instructora de matemáticas en City College de San Francisco
 Grace Imson, MA
Grace Imson, MA
Instructora de matemáticas en City College de San FranciscoObserva el orden de los términos para determinar el numerador y denominador en un problema con palabras. El primer término generalmente es el numerador y el segundo, el denominador. Por ejemplo, si un problema solicita la relación entre la longitud y el ancho de un elemento, la longitud será el numerador, mientras que el ancho, el denominador.
Anuncio
Parte 3
Parte 3 de 3:Encontrar errores
-
1Evita sumar o restar o resta problemas de palabras en proporciones. Muchos problemas de palabras se ven así: "Una receta necesita 4 papas y 5 zanahorias. Si quieres utilizar 8 papas en lugar de 5, cuántas zanahorias se necesita para mantener la proporción igual?". Muchos estudiantes tratan de añadir la misma cantidad de cada cantidad. En realidad se necesita utilizar una multiplicación, no una suma, para mantener la proporción igual. He aquí un ejemplo del mal y correcta de resolver este ejemplo:
- Método incorrecto: "8 - 4 = 4, por lo que se añadió 4 papas a la receta. Eso significa que se debe tomar las 5 zanahorias y añadir 4 a eso también...¡espera! Así no espere cómo funcionan las proporciones. Lo intentaré nuevo".
- Método correcto: "8 ÷ 4 = 2, así que se multiplica el número de papas por 2. Eso significa que se debería multiplicar las 5 zanahorias por 2 también 5 x 2 = 10, por lo que se necesitan 10 zanahorias en total para la nueva receta".
-
2Haz la conversión a las mismas unidades. Algunos problemas de palabras se complican por el cambio a una unidad diferente. Haz la conversión a la misma unidad antes de encontrar la proporción. Este es un ejemplo de un problema y su solución:
- Un dragón tiene 500 gramos de oro y 10 kilogramos de plata. ¿Cuál es la proporción de oro y plata en el tesoro del dragón?
- Los gramos y los kilogramos no son la misma unidad, por lo que se tiene que convertir. 1 kilogramo = 1.000 gramos, por lo que 10 kilogramos = 10 kilogramos x = 10 x 1.000 gramos = 10.000 gramos .
- El dragón tiene 500 gramos de oro y 10.000 gramos de plata.
- La proporción de oro a la plata es .
-
3Escribe las unidades en el problema. En problemas de palabras de proporciones, es mucho más fácil de detectar errores si escribes las unidades después de cada valor. Recuerda que la misma unidad en la parte superior e inferior de una fracción se anula. Después de cancelar tanto como sea posible, se debe terminar con las unidades adecuadas para la respuesta.
- Problema de ejemplo: si tiene 6 cajas y en cada 3 cajas hay nueve canicas, ¿cuántas canicas tienes?
- Método incorrecto: Espera, nada se cancela, así que mi respuesta sería "cajas x cajas / canícas."
- Método correcto:
18 canicas.
CONSEJO DE ESPECIALISTAGrace Imson es una maestra de matemáticas con más de 40 años de experiencia docente. Actualmente, Grace es instructora de matemáticas en el City College de San Francisco, y anteriormente trabajó en el Departamento de Matemáticas de la Universidad de Saint Luois. Ha enseñado matemáticas en los niveles de primaria, secundaria, preparatoria y universidad. Tiene una maestría en Educación, con una especialización en Administración y Supervisión de la Universidad de Saint Louis.Instructora de matemáticas en City College de San Francisco
 Grace Imson, MA
Grace Imson, MA
Instructora de matemáticas en City College de San FranciscoUn problema común es saber qué número usar como numerador. En un problema de palabras, el primer término establecido generalmente es el numerador, mientras que el segundo, el denominador. Si quieres saber la relación entre longitud y el ancho de un elemento, la longitud es el numerador, mientras que el ancho, el denominador.
Anuncio
Referencias
- ↑ http://www.virtualnerd.com/common-core/grade-6/6_RP-ratios-proportional-relationships/A
- ↑ http://www.purplemath.com/modules/ratio.htm
- ↑ http://www.helpwithfractions.com/math-homework-helper/least-common-denominator/
- ↑ http://www.mathplanet.com/education/algebra-1/how-to-solve-linear-equations/ratios-and-proportions-and-how-to-solve-them
- ↑ http://www.math.com/school/subject1/lessons/S1U2L2DP.html
Acerca de este wikiHow
Para calcular una proporción, empieza por determinar qué cantidades vas a comparar entre sí. Por ejemplo, si quieres conocer la proporción de niñas respecto a la de niños en una clase donde hay 5 niñas y 10 niños, entonces las cantidades a comparar serían 5 y 10. Luego agrega dos puntos o la palabra "a" para expresarlo como una proporción. En este ejemplo, sería "5 a 10" o "5:10". Por último, si es posible, simplifica la proporción dividiendo ambos números entre el máximo factor común.