Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 22 502 veces.
Aunque los logaritmos parezcan difíciles de usar, es solo cuestión de aprender las técnicas correctas, como ocurre con los exponentes o los polinomios. Para dividir dos logaritmos que tengan la misma base o expandir un logaritmo que contenga un cociente, solo debes conocer unas cuantas propiedades básicas.
Pasos
Método 1
Método 1 de 2:Dividir logaritmos a mano
-
1Revisa para ver si hay números negativos y unos. Este método abordará los problemas que tengan la forma , aunque hay ciertos casos especiales en los que esto no funciona:[1]
- El logaritmo de un número negativo es indefinido en todas las bases (como o ). En este caso, debes escribir "no hay solución".
- El logaritmo de cero también es indefinido en todas las bases. Si te encuentras con un término como , también debes escribir "no hay solución".
- El logaritmo de 1 en cualquier base () siempre es igual a cero. Esto se debe a que para todos los valores de x. En este caso, en lugar de usar el método a continuación, reemplaza este logaritmo por 1.
- Si dos logaritmos tienen bases diferentes, como en el caso de , y ninguno de ellos puede simplificarse hasta obtener un número entero, el problema no podrá resolverse a mano.
-
2Convierte la expresión en un logaritmo. Ahora, puedes simplificar el problema hasta obtener un solo logaritmo (asumiendo que no aplique ninguna de las excepciones mencionadas anteriormente). Para ello, emplea la fórmula .
- Ejemplo 1: resuelve .
Para empezar, conviértelo en un solo logaritmo mediante la fórmula anterior: . - Esta es la fórmula para el "cambio de base" que se obtiene a partir de las propiedades logarítmicas básicas.
- Ejemplo 1: resuelve .
-
3Realiza el cálculo a mano de ser posible. Recuerda que debes considerar la expresión "" o "¿A qué exponente puedo elevar a para obtener x?" para poder resolver . Ten en cuenta que esto no siempre podrá resolverse sin usar una calculadora pero, con suerte, quizás obtengas un logaritmo que pueda simplificarse fácilmente.
- Ejemplo 1 (cont.): reescribe como . La respuesta al problema es el valor de "?" pero es posible que debas aplicar el ensayo y error para encontrarlo:
La respuesta que buscabas era 16, por lo que = 4.
- Ejemplo 1 (cont.): reescribe como . La respuesta al problema es el valor de "?" pero es posible que debas aplicar el ensayo y error para encontrarlo:
-
4Deja la respuesta en forma de logaritmo si no puedes simplificarla. Es muy difícil resolver algunos logaritmos a mano, por lo que, si necesitas la respuesta para fines prácticos, quizás debas usar una calculadora. En cambio, si vas a resolver el problema para una clase de matemáticas, es probable que el profesor espere que la respuesta quede en forma de logaritmo. Este es otro ejemplo de la aplicación de este método a un problema más difícil:
- Ejemplo 2: ¿cuánto es ?
- Conviértelo en un solo logaritmo: . (Observa que, en cada logaritmo inicial, el 3 desaparece, lo cual aplica también para todas las bases).
- Reescríbelo como y prueba algunos valores posibles para "?":
El 58 se encuentra entre ambos números, por lo que ninguna de las respuestas de será un número entero. - Deja la respuesta como .
Anuncio
Método 2
Método 2 de 2:Trabajar con el logaritmo de un cociente
-
1Empieza con un problema de división dentro de un logaritmo. Esta sección te enseñará a resolver problemas que contengan expresiones en la forma .
- Por ejemplo, empieza con el siguiente problema:
"Encuentra el valor de n si ".
- Por ejemplo, empieza con el siguiente problema:
-
2Revisa para ver si hay números negativos. El logaritmo de un número negativo es indefinido, por lo que, si x o y son números negativos, debes confirmar que el problema tenga una solución antes de poder continuar.
- Si x o y es un número negativo, el problema no tendrá solución.
- Si ambas son números negativos, emplea la propiedad para eliminar los signos.
- El problema del ejemplo no contiene logaritmos de números negativos, por lo que puedes ir al siguiente paso.
-
3Expande el cociente hasta obtener dos logaritmos. La fórmula describe una propiedad útil de los logaritmos, la cual establece que el logaritmo de un cociente siempre equivaldrá al logaritmo del numerador menos el logaritmo del denominador.[2]
- Emplea esta fórmula para expandir el lado izquierdo del problema:
. - Reemplaza el resultado en la ecuación original:
→
.
- Emplea esta fórmula para expandir el lado izquierdo del problema:
-
4Simplifica los logaritmos si puedes. Si la respuesta de cualquiera de los logaritmos nuevos en la expresión es un número entero, puedes simplificarlos en este paso.
- En el problema del ejemplo, hay un término nuevo: . 33 = 27, por lo que puedes simplificar hasta obtener 3.
- Ahora, la ecuación completa es como sigue:
-
5Aísla la variable. Te será útil aislar el término que contenga la variable a un lado de la ecuación, como lo harías en cualquier problema de álgebra. En donde sea posible, simplifica la ecuación combinando términos similares.
-
.
-
-
6Emplea las propiedades adicionales de los logaritmos según sea necesario. Si quieres aislar la variable de los demás términos dentro del mismo logaritmo, puedes reescribir el término mediante otras propiedades logarítmicas.
- En el problema del ejemplo, n aún se encuentra atrapado dentro de .
Emplea la propiedad del producto de los logaritmos para aislar n:
- Reemplaza el resultado en la ecuación completa:
- En el problema del ejemplo, n aún se encuentra atrapado dentro de .
-
7Sigue simplificando hasta obtener la solución. Resuelve el problema empleando nuevamente las mismas técnicas algebraicas y logarítmicas. Si la solución del problema no es un número entero, redondea a la cifra significativa más cercana con una calculadora.
-
39 = 19 683, por lo que n = 19 683.
Anuncio -
















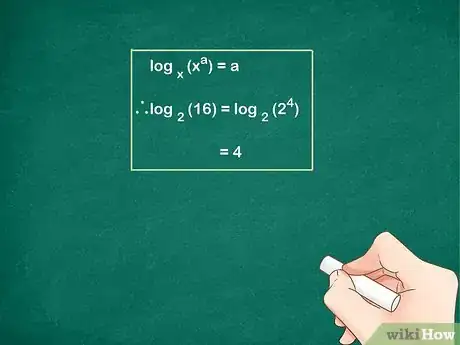



















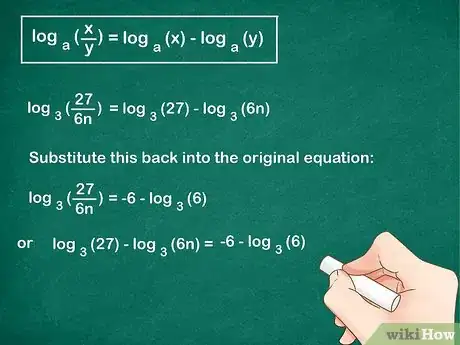



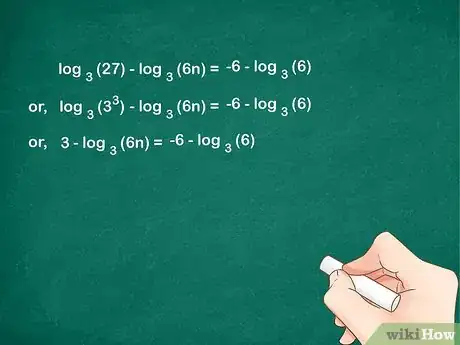


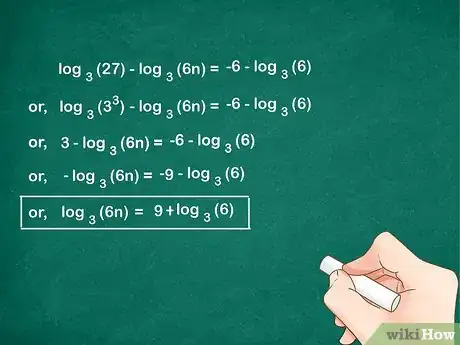


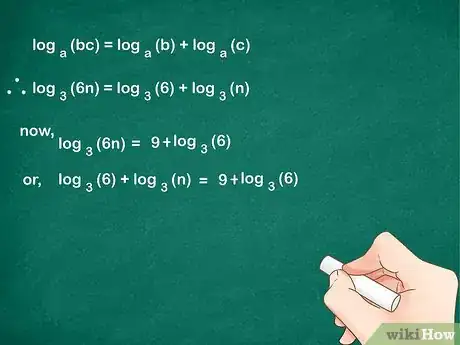




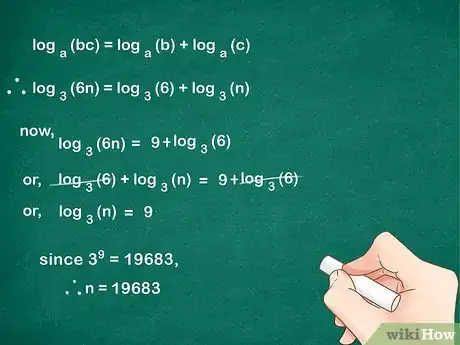




















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 22 502 veces.