Cómo encontrar el recíproco

Información del autor

Los recíprocos son útiles para todo tipo de ecuaciones algebraicas. Por ejemplo: cuando divides una fracción entre otra, multiplicas la primera por el recíproco de la segunda. Los recíprocos también podrían ser necesarios al operar ecuaciones lineales.

Método 1

Método 1 de 3:
Encuentra el recíproco de un número entero o fracción

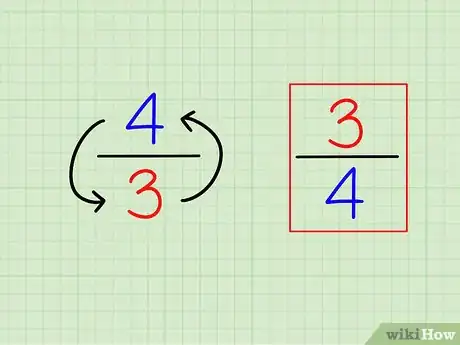
1
Encuentra el recíproco de una fracción dándole la vuelta. La definición de "recíproco" es simple. Para encontrar el recíproco de cualquier número, simplemente calcula "1 ÷ (ese número)". Para una fracción, el recíproco es solo una fracción diferente, con los números "al revés" (invertida).^{[1]
X
Fuente de investigación}
- Por ejemplo: el recíproco de ³/₄ es ⁴/₃.
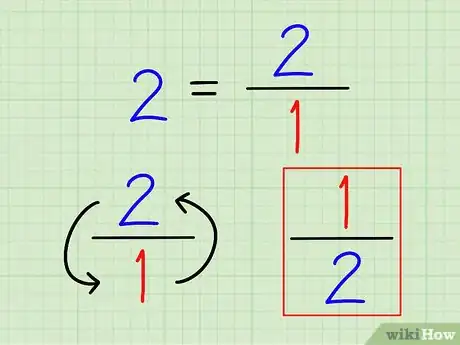
2
Escribe el recíproco de un número entero como una fracción. Una vez más, el recíproco de un número siempre es 1 ÷ (ese número). Para un número entero, escríbelo como fracción; no hay porqué calcularlo de forma decimal.
- Por ejemplo: el recíproco de 2 es 1 ÷ 2 = ¹/₂.
Anuncio

Método 2

Método 2 de 3:
Encuentra el recíproco de un número mixto

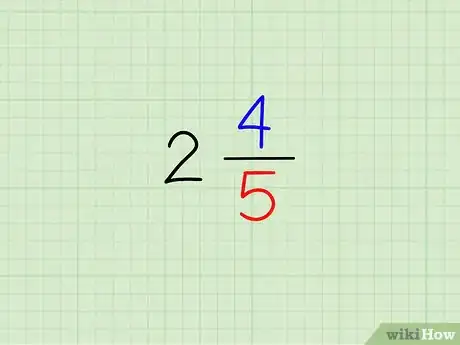
1
Identifica un número mixto. Los números mixtos están compuestos por un entero y una fracción, como 2⁴/₅. Hay dos pasos para encontrar el recíproco de un número mixto, los cuales se explican a continuación.
2
Cámbialo a una fracción impropia. Recuerda que el número 1 siempre puede escribirse como (número)/(el mismo número) y las fracciones con el mismo denominador (el número inferior) pueden sumarse. Este es un ejemplo con 2⁴/₅:
- 2⁴/₅
- = 1 + 1 + ⁴/₅
- = ⁵/₅ + ⁵/₅ + ⁴/₅
- = ^(5+5+4)/₅
- = ¹⁴/₅.
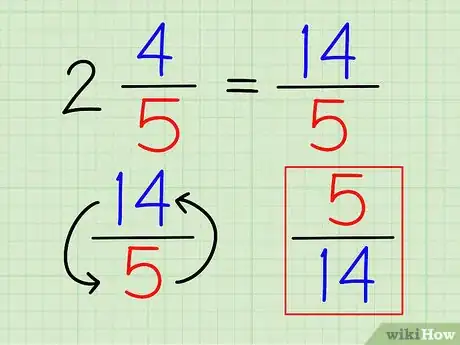
3
Dale vuelta a la fracción. Una vez que el número esté escrito completamente en forma de fracción, puedes encontrar el recíproco como lo harías con cualquier fracción: dándole la vuelta.
- En el ejemplo anterior, el recíproco de ¹⁴/₅ es ⁵/₁₄.
Anuncio

Método 3

Método 3 de 3:
Encuentra el recíproco de un decimal

1
De ser posible, conviértelo en una fracción. Puedes reconocer algunos números decimales comunes que pueden convertirse fácilmente en fracciones. Por ejemplo: 0,5 = ¹/₂ y 0,25 = ¹/₄. Una vez que lo hayas convertido en fracción, simplemente dale la vuelta a la fracción para encontrar el recíproco.
- Por ejemplo: el recíproco de 0,5 es ²/₁ = 2.
2
Escribe un problema de división. Si no puedes convertirlo en fracción, calcula el recíproco de ese número con un problema de división: 1 ÷ (el decimal). Puedes usar una calculadora para resolverlo o continuar con el siguiente paso para resolverlo a mano.
- Por ejemplo: puedes encontrar el recíproco de 0,4 calculando 1 ÷ 0,4.
3
Cambia la división para usar números enteros. El primer paso para dividir decimales es mover la coma o el punto decimal hasta que todos los números involucrados sean números enteros. Siempre y cuando muevas la coma decimal el mismo número de espacios para ambos números, obtendrás la respuesta correcta.
- Por ejemplo: puedes tomar 1 ÷ 0,4 y reescribirlo como 10 ÷ 4. En este caso, se movió cada lugar decimal un espacio a la derecha, que es lo mismo que multiplicar ambos números por diez.
4
Resuelve el problema con una división larga. Usa las técnicas de una división larga para calcular el recíproco. Si calculas 10 ÷ 4, obtendrás la respuesta 2.5, que es el recíproco de 0,4.

Anuncio

Consejos

Un número recíproco negativo es el mismo que el recíproco regular, multiplicado por un uno negativo.^{[2]
X
Fuente de investigación} Por ejemplo: el recíproco negativo de ³/₄ es -⁴/₃.
A veces, el recíproco se llama "inverso multiplicativo".^{[3]
X
Fuente de investigación}
El número 1 es su propio recíproco, ya que 1 ÷ 1 = 1.
El número 0 no tiene recíproco, ya que 1 ÷ 0 es indefinido.^{[4]
X
Fuente de investigación}