Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 9586 veces.
Las funciones racionales son funciones matemáticas (ecuaciones) que muestran la relación entre dos polinomios.[1] Esto significa que siempre existe algún tipo de fracción con más que solo los coeficientes. Por lo tanto, no es una función racional porque la única fracción es un término de coeficiente. Sin embargo, es una fracción racional. Las asíntotas verticales son una representación de los valores que no son una solución a la ecuación, pero que ayudan a definir el gráfico de soluciones.[2]
Pasos
Parte 1
Parte 1 de 2:Encontrar asíntotas verticales
-
1Factoriza el denominador de la función. Para simplificar la función, primero debes desglosar el denominador en factores, tanto como sea posible. A los fines de encontrar las asíntotas, puedes ignorar los numeradores.[3]
- Por ejemplo, supón que tienes la función . El denominador se puede factorizar en dos términos .
- Otro ejemplo: toma la función . Aquí el denominador se puede reconocer como una simple función cuadrática, la cual se puede factorizar en .
- Ten presente que algunas funciones del denominador no se pueden factorizar. Por ejemplo, en la ecuación la función del denominador, , no se puede factorizar. En este primer paso solo hay que dejarla como está.
- Si necesitas repasar la factorización de funciones, consulta este wikiHow sobre factorización de ecuaciones algebraicas o este otro sobre factorización de ecuaciones cuadráticas.
-
2Encuentra los valores para los cuales el denominador es igual a 0. Sin prestar atención todavía al numerador de la función, iguala a cero el denominador factorizado y resuelve la ecuación para encontrar el valor de x. Recuerda que los factores son términos que se multiplican, por lo puedes resolver el problema igualando cualquiera de los factores a 0. Puedes encontrar una o más soluciones dependiendo de la cantidad de factores que existan.
- Por ejemplo, si luego de factorizar la función del denominador obtienes , entonces puedes igualarlo a 0 así: . Las soluciones serán todos los valores de x para los cuales esto sea verdadero. Para encontrar estos valores, deberás igualar a 0 cada uno de los factores individuales. Así obtendrás dos problemas menores: y . La primera solución es y la segunda .
- Como segundo ejemplo, imagina que tienes el denominador . Esto se puede factorizar en dos términos: . Al igualar cada factor a 0 obtendrás y . Por consiguiente, las soluciones al problema serán y .
-
3Aprende a interpretar las soluciones. El trabajo que has hecho hasta aquí consiste en identificar los valores de x para los cuales el denominador de la función es igual a 0. Ten presente que una función racional es un problema de división larga en el cual el valor del numerador se divide entre el valor del denominador. Como la división entre 0 es una indeterminación, cualquier valor de x para el cual el denominador sea igual a 0 representa una asíntota vertical para toda la función.Anuncio
Parte 2
Parte 2 de 2:Graficar asíntotas verticales
-
1Repasa el significado de gráfico. El gráfico de una función es una representación visual de los valores de y que son soluciones a una ecuación dada. El gráfico puede consistir en puntos individuales, una línea recta, una línea curva o incluso algunas figuras cerradas como un círculo o una elipse. Cualquier punto que coincida con la línea podría ser una solución a la ecuación.[4]
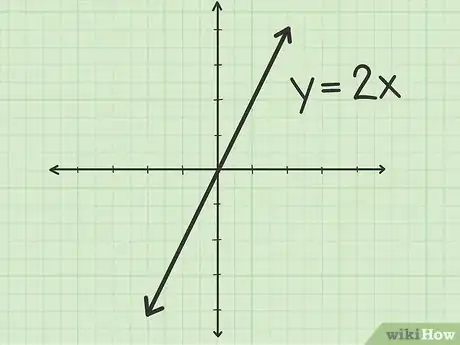
- Por ejemplo, que una ecuación simple, tendrá infinitas soluciones. Expresadas como pares de (x,y), algunas de esas posibles soluciones son (1,2), (2,4), (3,6) o cualquier par de números en los cuales el segundo de ellos sea el doble del primero. Al representar estos puntos en el plano de coordenadas x,y se formará una línea recta continua similar a una diagonal que va hacia arriba de izquierda a derecha. Para ver más ejemplos de tipos de gráficos puedes consultar este wikiHow.
- Una ecuación cuadrática es aquella que tiene un exponente de 2 como, por ejemplo, . Algunos ejemplos de soluciones serían (-1,-2), (0,-1), (1,1) y (2,7). Si graficas estos puntos (y otros) obtendrás el gráfico de una parábola, que es una curva en forma de U. Si quieres repasar este tipo de gráficos, puedes consultar este wikiHow.
- Si necesitas más ayuda para aprender a graficar funciones, lee este wikiHow sobre funciones en general o este otro sobre funciones racionales.
-
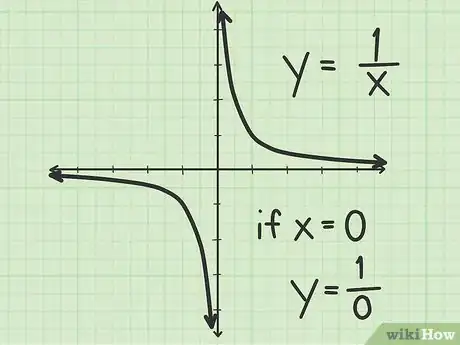
2Identifica las asíntotas. Una asíntota es una línea recta que generalmente se usa como una especie de límite para el gráfico de una función. Una asíntota puede ser vertical, horizontal o de cualquier ángulo. Representa valores que no son soluciones a la ecuación, pero podría ser un límite para las soluciones.[5]
- Por ejemplo, supón que tienes la ecuación . Si comienzas por el valor x=3 y te desplazas hacia abajo para seleccionar algunas soluciones para esta ecuación, obtendrás (3, 1/3), (2, 1/2) y (1, 1). Si sigues desplazándote hacia abajo, el próximo valor para x sería 0, pero así crearías la fracción y=1/0. Debido a que la división entre 0 es una indeterminación, no puede ser una solución a esta función. Por lo tanto, el valor x=0 es una asíntota vertical para esta ecuación.
-
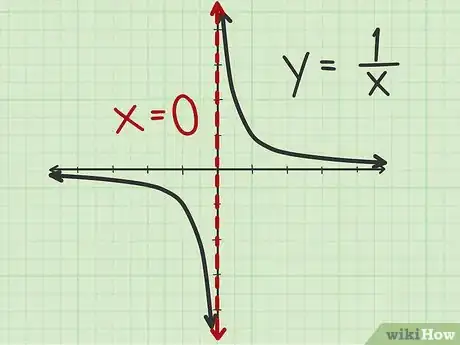
3Grafica las asíntotas verticales con una línea punteada. Por convención, cuando se dibuja la solución a una función y dicha función tiene una asíntota vertical, tienes que graficarla dibujando una línea punteada en el valor correspondiente. En el caso de , deberás hacer una línea vertical punteada en x=0.Anuncio
Referencias
- ↑ http://www.mathsisfun.com/definitions/rational-function.html
- ↑ http://www.softschools.com/math/calculus/finding_vertical_asymptotes_of_rational_functions/
- ↑ http://www.montereyinstitute.org/courses/Algebra1/COURSE_TEXT_RESOURCE/U11_L1_T1_text_final.html
- ↑ https://artofproblemsolving.com/wiki/index.php/Graph_of_a_function
- ↑ https://www.khanacademy.org/math/old-ap-calculus-ab/ab-limits-continuity/ab-infinite-limits/v/limits-and-infinity






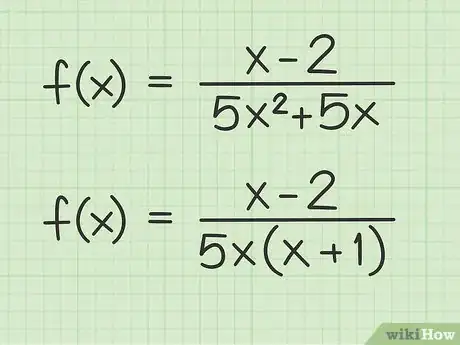







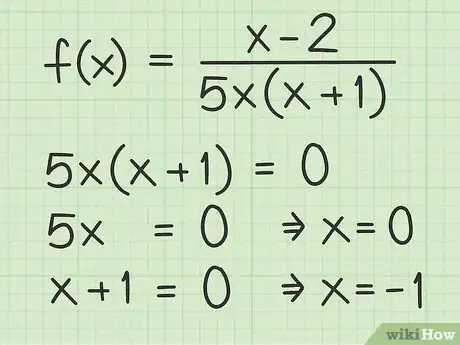











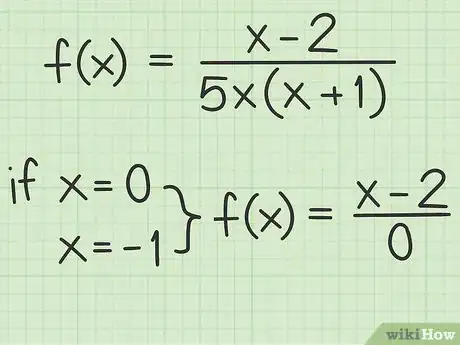
























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 9586 veces.