wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 14 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo.
Este artículo ha sido visto 141 369 veces.
Pasos
-
1Aprende a identificar las diferencias entre ecuaciones logarítmicas y exponenciales. Este primer paso es muy sencillo. Si contiene un logaritmo (por ejemplo: logax = y) es un problema logarítmico. Un logaritmo está designado por las letras "log". Si la ecuación contiene un exponente (que es una variable elevada a una potencia), es una ecuación exponencial. Un exponente es un número superíndice colocado después de un número.
- Logarítmico: logax = y
- Exponencial: ay= x
-
2Identifica las partes de un logaritmo. La base es el número superíndice encontrado después de las letras "log" --2 en este ejemplo. El argumento o número es el número que sigue al número superíndice --8 en este ejemplo. Por último, la respuesta es el número con el que se iguala la expresión logarítmica--3 en esta ecuación.[2]
-
3Identifica la diferencia entre un logaritmo común y uno natural.
- Los logaritmos comunes tienen una base de 10 (por ejemplo, log10x). Si el logaritmo se escribe sin una base (como log x), entonces asume que tiene base de 10.
- Los logaritmos naturales, o neperianos tienen una base e. La "e" es una constante matemática que es igual al límite de (1 + 1/n)ncuando n se acerca al infinito, aproximadamente 2,718281828 (tiene muchos más dígitos que los escritos aquí). logex se escribe a menudo como ln x.
- Los demás tipos de logaritmos tienen otra base diferente a aquella de los logaritmos comunes y la constante matemática e. Los logaritmos binarios tienen una base de 2 (por ejemplo, log2x). Los logaritmos hexadecimales tienen una base de 16 (por ejemplo log16x (o log#0fx en la notación hexadecimal). Los logaritmos que tienen la base 64a son más complejos y por lo tanto se restringen al dominio de la geometría computarizada avanzada.
-
4Aprende y aplica las propiedades de los logaritmos. Las propiedades de los logaritmos permiten que resuelvas ecuaciones logarítmicas y exponenciales que de otra manera sería imposible. Esto solo funciona si la base "a" y el argumento son positivos. También la base "a" no puede ser 1 o 0. Las propiedades de los logaritmos se enumeran a continuación con un ejemplo por separado para cada uno con números en lugar de variables. Estas propiedades se usan cuando se resuelven ecuaciones.
- loga(xy) = logax + logay
El logaritmo de dos números, "x" e "y", que se multiplican entre sí se pueden dividir en dos logaritmos separados: un logaritmo para cada uno de los factores que son sumados (también funciona a la inversa).
Ejemplo:
log216 =
log28*2 =
log28 + log22 - loga(x/y) = logax - logay
El logaritmo de dos números se dividen entre sí, "x" e "y", puede dividirse en dos logaritmos: el logaritmo del dividendo de cada uno, "x" e "y", pueden dividirse en dos logaritmos: el logaritmo del dividendo "x" menos el logaritmo del divisor "y".
Ejemplo:
log2(5/3) =
log25 - log23 - loga(xr) = r*logax
Si el argumento "x" de un logaritmo tiene un exponente "r", el exponente puede moverse al frente del logaritmo.
Ejemplo:
log2(65)
5*log26 - loga(1/x) = -logax
Piensa en el argumento. (1/x) es igual a x-1. Básicamente esta es otra versión de la propiedad anterior.
Ejemplo:
log2(1/3) = -log23 - logaa = 1
Si la base "a" iguala el argumento "a", la respuesta es 1. Esto es muy sencillo de recordar si uno piensa en el logaritmo en forma exponencial. ¿Cuántas veces se debe multiplicar "a" por sí misma para obtener "a"? Una vez.
Ejemplo:
log22 = 1 - loga1 = 0
Si el argumento es 1, la respuesta siempre será cero. Esta propiedad es cierta debido a que cualquier número con un exponente cero es igual a 1.
Ejemplo:
log31 =0 - (logbx/logba) = logax
Esto se conoce como "cambio de la base".[3] Un logaritmo dividido por otro, ambos con la misma base "b", es igual a un logaritmo sencillo. El argumento "a" del denominador se convierte en la base nueva y el argumento "x" del numerador se convierte en el argumento nuevo. Esto es sencillo de recordar si piensas en la base como el fondo del objeto y que el denominador es el fondo de una fracción.
Ejemplo:
log25 = (log 5/log 2)
Anuncio - loga(xy) = logax + logay
Practica utilizando las propiedades. Estas propiedades se memorizan mejor con el uso repetido al resolver ecuaciones. El siguiente ejemplo es una ecuación que se resuelve mejor con una de las propiedades:4x*log2 = log8 Divide ambos lados por log2.4x = (log8/log2) Usa el cambio de la base.4x = log28 Calcula el valor del logaritmo.4x = 3 Divide ambos lados por 4. x = 3/4 Resuelto. Esto es muy útil. Verás que entenderás los logaritmos.
Consejos
- La regla mnemónica "2.7jacksonjackson" es útil para recordar e. 1828, el año cuando Andrew Jackson fue elegido, así que la regla mnemónica es para 2.718281828.
Referencias
- ↑ Usar y derivar propiedades algebraicas de los logaritmos, http://people.hofstra.edu/Stefan_Waner/Realworld/calctopic1/logs.html
- ↑ Logaritmos: centro de recursos NDT, http://www.ndt-ed.org/EducationResources/Math/Math-Logs.htm
- ↑ Logaritmos: Wikipedia




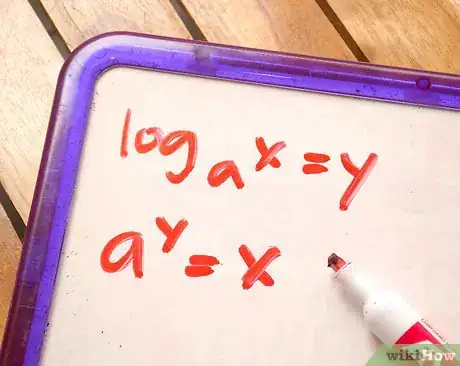
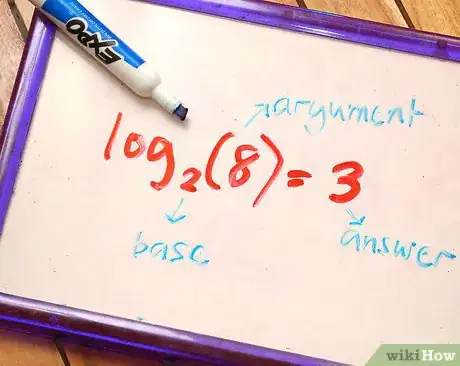
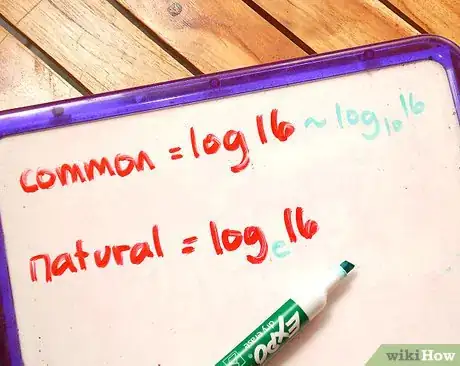
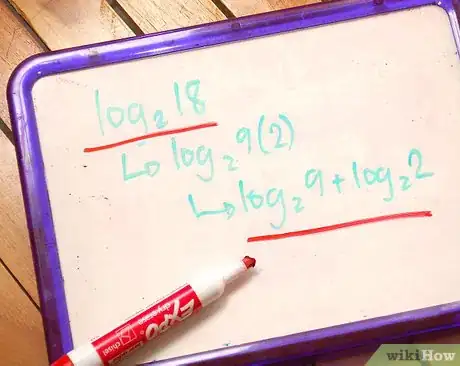




-Step-31-Version-2.webp)