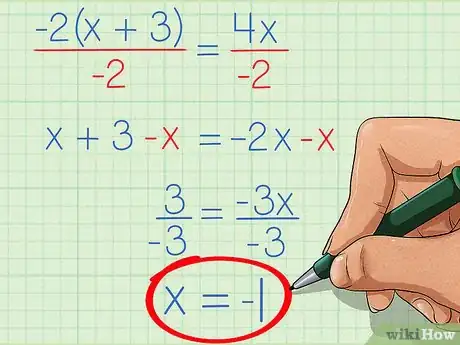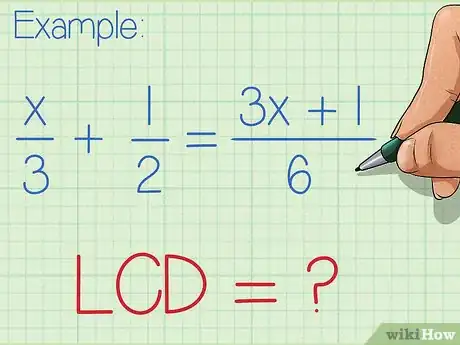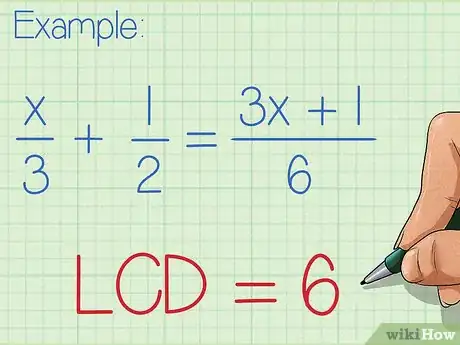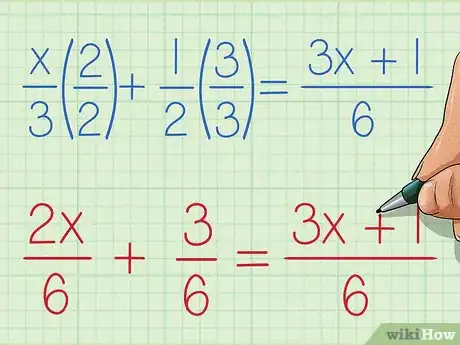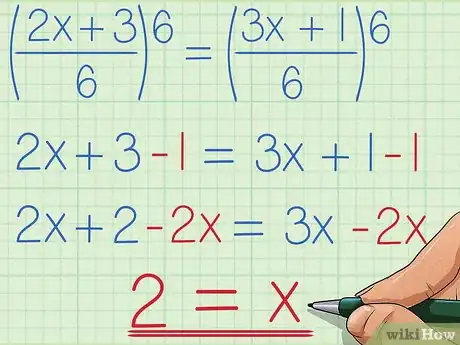Cómo resolver ecuaciones racionales

Información del autor

Una expresión racional es una fracción con una o más variables en el numerador o el denominador. Una “ecuación” racional es cualquier ecuación que tenga por lo menos una expresión racional. Al igual que las ecuaciones algebraicas normales, las ecuaciones racionales se resuelven realizando las mismas operaciones en ambos lados de la ecuación hasta que la variable quede aislada a un lado del signo de igual. Hay dos técnicas especiales que son extremadamente útiles para aislar las variables y resolver las ecuaciones racionales, la multiplicación cruzada y encontrar el mínimo común denominador.

Método 1

Método 1 de 2:
Multiplicación cruzada

1
Si es necesario, reorganiza tu ecuación para tener una fracción en cada lado del signo de igual. La multiplicación cruzada es una forma fácil y rápida de resolver ecuaciones racionales. Lamentablemente, este método solo funciona con ecuaciones racionales que contienen exactamente una expresión racional o una fracción en cada lado del signo de igual. Si tu ecuación no está en forma de multiplicación cruzada, entonces quizás necesites utilizar operaciones algebraicas para mover los términos a su lugar apropiado.
- Por ejemplo, la ecuación (x + 3)/4 - x/(-2) = 0 puede reorganizarse fácilmente en forma de multiplicación cruzada agregando x/(-2) en ambos lados de la ecuación, dejándonos con (x + 3)/4 = x/(-2).
  - Ten en cuenta que los decimales y los números enteros pueden convertirse en fracciones agregándoles un 1 de denominador. La ecuación (x + 3)/4 - 2.5 = 5, por ejemplo, puede reescribirse como (x + 3)/4 = 7.5/1, para poder resolverse por el método de multiplicación cruzada.
- Algunas ecuaciones racionales no se pueden reducir fácilmente a una forma con una fracción o una ecuación racional en cada lado del signo de igual, en esos casos, utiliza el método del mínimo común denominador.
2
Multiplicación cruzada. Multiplicación cruzada simplemente significa multiplicar el numerador de una fracción por el denominador de la otra y viceversa. Multiplica el numerador de la fracción de la izquierda del signo de igual por el denominador de la derecha. Repite con el numerador de la fracción del lado derecho y el denominador de la fracción del lado izquierdo.
- El método de multiplicación cruzada funciona de acuerdo a las bases de los principios algebraicos. Las expresiones racionales y otras fracciones pueden convertirse a decimales multiplicándolos por sus denominadores. La multiplicación cruzada básicamente es un atajo útil para multiplicar ambos lados de la ecuación por ambos denominadores de las fracciones. ¿No lo crees? Inténtalo (obtendrás los mismos resultados después de simplificar).
3
Define los dos productos como iguales entre sí. Después de la multiplicación cruzada tendrás dos productos. Define esos dos términos como iguales entre sí y simplifica para llevar a cada lado de la ecuación a sus términos más simples.
- Por ejemplo, si tu expresión racional original era (x+3)/4 = x/(-2), después de la multiplicación cruzada, tu nueva ecuación es -2(x+3) = 4x. Si queremos, también la podemos escribir así -2x - 6 = 4x.
4
Resuelve para tu variable. Utiliza operaciones algebraicas para resolver la variable en tu ecuación. Recuerda que si x aparece en ambos lados del signo de igual, entonces tendrás que sumar o restar los términos de x en ambos lados para tener los términos de x en un solo lado del signo de igual.
- En nuestro ejemplo, podemos dividir ambos lados de la ecuación entre -2, lo que nos da como resultado x+3 = -2x. Si restamos x a ambos lados, tenemos como resultado 3 = -3x. Finalmente, dividimos ambos lados entre -3, lo que nos da -1 = x, que lo podemos reescribir como x = -1. Ya encontramos x y resolvimos nuestra ecuación racional.

Método 2

Método 2 de 2:
Mínimo común denominador (MCD)

1
Conoce cuándo es apropiado encontrar el “Mínimo Común Denominador”. El mínimo común denominador (MCD) puede utilizarse para simplificar ecuaciones racionales, haciendo posible resolver sus variables. Encontrar el MCD es una buena idea cuando tu ecuación racional no puede escribirse fácilmente de forma que tenga una (y solo una) fracción o expresión racional en cada lado del signo de igual. Para resolver ecuaciones racionales con tres o más términos, el MCD es una herramienta útil. Sin embargo, para resolver ecuaciones racionales con solo dos términos, el método de multiplicación cruzada puede ser más rápido.
2
Examina el denominador de cada fracción. Identifica cuál es el número más bajo que puede dividir equitativamente a cada denominador. Este es el MCD de tu ecuación.
- Algunas veces el mínimo común denominador (esto es, el número menor que tiene cada uno de los denominadores como factor) es obvio. Por ejemplo, si tu expresión es x/3 + 1/2 = (3x+1)/6, no es difícil ver que el número menor con 3, 2 y 6 como factor es 6.
- A menudo, sin embargo, el MCD de una ecuación racional no es tan obvio. En estos casos, intenta examinar los múltiplos del denominador más grande hasta que encuentres un número que tenga a todos los denominadores menores como factor. En ocasiones, el MCD es un múltiplo de dos de los denominadores. Por ejemplo, en la ecuación x/8 + 2/6 = (x - 3)/9 el MCD es 8*9 = 72.
- Si uno o más de los denominadores de las fracciones contiene una variable, el proceso es más complicado, pero no imposible. En estos casos, el MCD será una expresión (que tenga las variables) que todos los denominadores puedan dividir, en vez de un número solo. Por ejemplo, en la ecuación 5/(x-1) = 1/x + 2/(3x), el MCD es 3x(x-1), porque cada denominador lo puede dividir equitativamente (si dividimos entre (x-1) da 3x, si lo hacemos entre 3x nos da (x-1) y si dividimos entre x da como resultado 3(x-1).
3
Multiplica cada fracción, en la ecuación racional por 1. Multiplicar cada término por 1 puede parecer inútil, sin embargo hay un truco. 1 puede definirse como cualquier número sobre sí mismo 2/2 y 3/3, por ejemplo, también son formas válidas de escribir "1." Éste método toma ventaja de su definición alternativa. Multiplicar cada fracción en tu ecuación racional por 1, escribiendo 1 cada vez que el número o el término que multiplica a cada denominador para dar el MCD por sí mismo.
- En nuestro ejemplo básico, podríamos multiplicar x/3 por 2/2 para obtener 2x/6 y multiplicar 1/2 por 3/3 para tener 3/6. 3x +1/6 ya tiene el 6, el MCD como su denominador, así que podemos multiplicarlo por 1/1 o dejarlo como está.
- En nuestro ejemplo con variables en el denominador de nuestras fracciones, el proceso es un poco más complicado. Debido a que nuestro MCD es 3x(x-1), multiplicamos cada expresión racional por el término que lo multiplica para obtener 3x(x-1) sobre sí mismo. Podríamos multiplicar 5/(x-1) por (3x)/(3x) para tener como resultado 5(3x)/(3x)(x-1), multiplicar 1/x por 3(x-1)/3(x-1) para obtener 3(x-1)/3x(x-1) y multiplicar 2/(3x) por(x-1)/(x-1) para tener 2(x-1)/3x(x-1).
4
Simplifica y resuelve para x. ahora que todos los términos en tu ecuación racional tienen el mismo denominador, puedes eliminar los denominadores de la ecuación y resolver los numeradores. Simplemente multiplica ambos lados de la ecuación para dejar los numeradores solos. Después utiliza operaciones algebraicas para dejar x (o cualquier variable que necesites encontrar) sola en un lado del signo de igual.
- En nuestro ejemplo básico, después de multiplicar cada término por formas alternativas de 1, obtenemos 2x/6 + 3/6 = (3x+1)/6. Dos fracciones pueden sumarse si tienen el mismo denominador, así que simplificamos la ecuación a (2x+3)/6 = (3x+1)/6 sin cambiar su valor. Multiplica ambos lados por 6 para cancelar los denominadores, lo que nos deja con 2x+3 = 3x+1. Resta 1 a ambos lados para obtener 2x+2 = 3x y resta 2x de ambos lados para obtener 2 = x, que puede escribirse como x = 2.
- En nuestro ejemplo con variables en los denominadores, nuestra ecuación después de multiplicar cada término por "1" es 5(3x)/(3x)(x-1) = 3(x-1)/3x(x-1) + 2(x-1)/3x(x-1). Multiplicar cada término por nuestro MCD nos permite cancelar los denominadores, dándonos como resultado 5(3x) = 3(x-1) + 2(x-1). Esto nos lleva a 15x = 3x - 3 + 2x -2, que se puede simplificar a 15x = x - 5. Si restamos x a ambos lados, obtenemos 14x = -5, que finalmente podemos simplificar a x = -5/14.

Consejos

Ten en cuenta que puedes escribir cualquier polinomio como una expresión racional, solo coloca el número “1” como denominador. De modo que x+3 y (x+3)/1 tienen el mismo valor, pero la segunda expresión se considera como una expresión racional, porque está escrita en forma de fracción.
Una vez que resuelvas para la variable en cuestión, revisa tu respuesta agregando el valor de la variable a la ecuación original. Si tienes el valor correcto de la variable, podrás simplificar la ecuación original a 1 = 1.