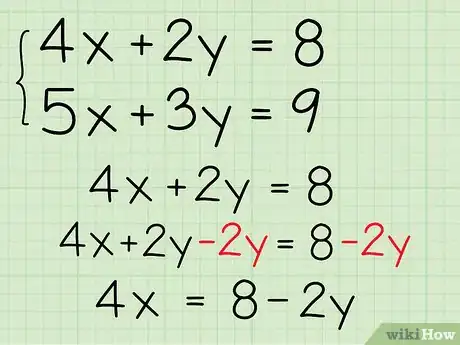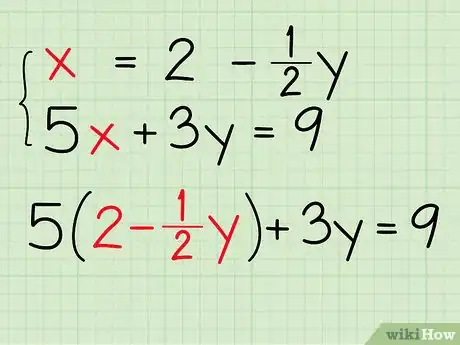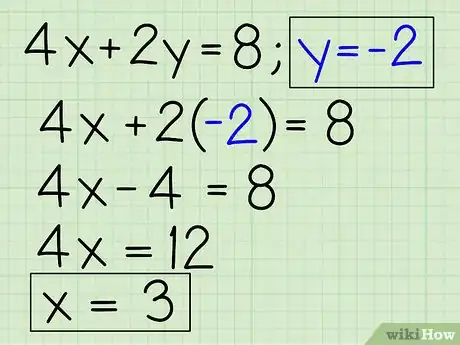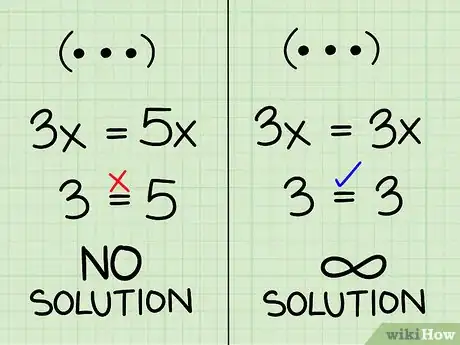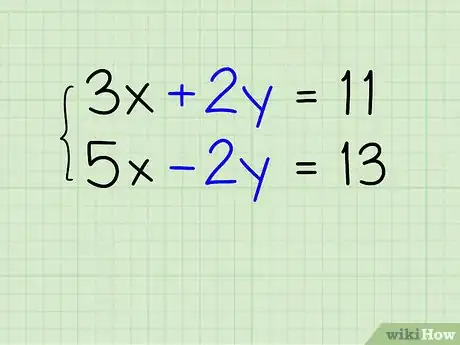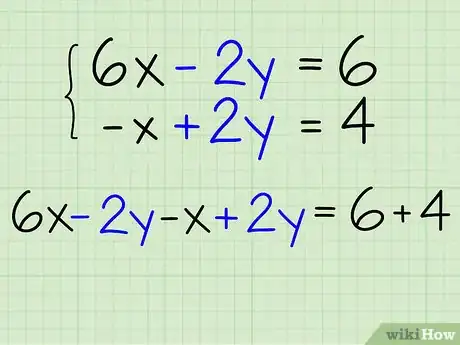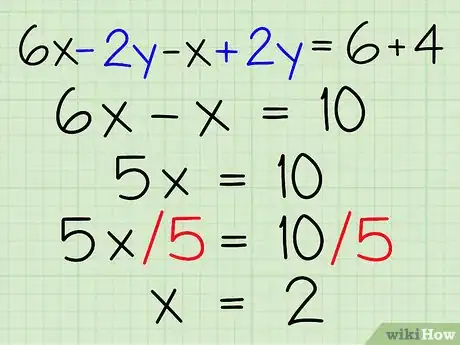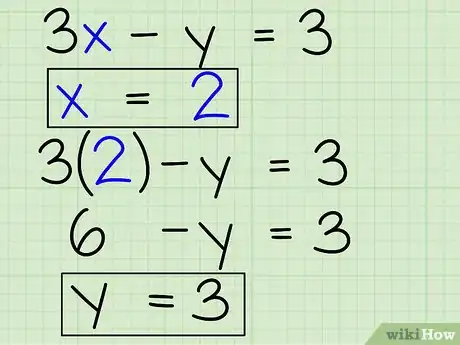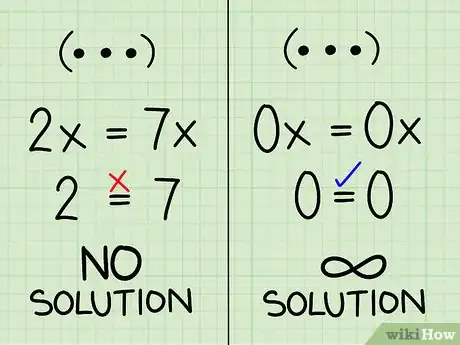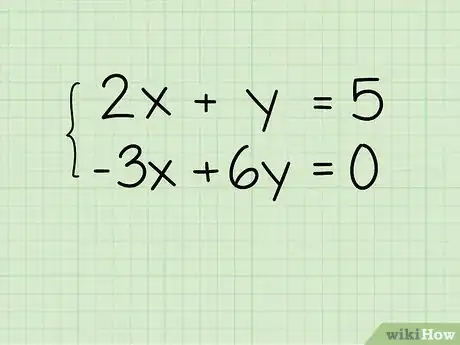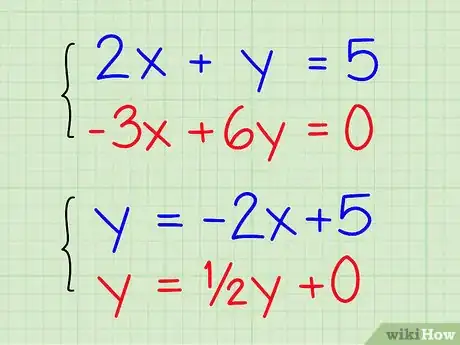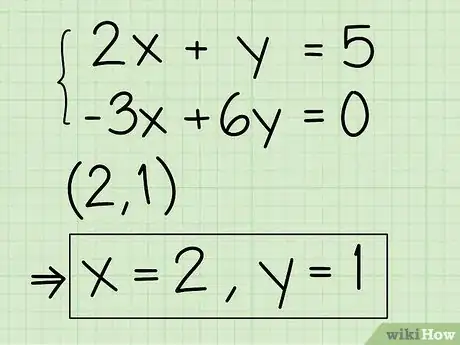Cómo resolver sistemas de ecuaciones lineales de dos variables

Información del autor

En un sistema de ecuaciones, hay que resolver dos o más ecuaciones al mismo tiempo. Si estas a su vez contienen dos variables distintas, tales como “x” e “y” (o incluso “a” y “b”), puede ser complicado a simple vista determinar la manera de resolverlas. Por suerte, una vez que sepas lo que tienes que hacer, lo único que necesitarás son algunas habilidades de álgebra básicas (y en ocasiones cierto conocimiento de fracciones) para poder resolver este problema. Si tu forma de aprender es visual o si tu maestro te lo solicita, es necesario que aprendas a graficar las ecuaciones. Graficarlas puede ser útil para “ver lo que sucede” o para verificar tu trabajo, pero puede ser un método más lento que otros y no funciona bien en todos los sistemas de ecuaciones.

Método 1

Método 1 de 3:
Método de sustitución

1
Mueve las variables a diferentes lados de la ecuación. Este método de “sustitución” empieza “resolviendo x” (o cualquier otra variable) en una de las ecuaciones. Por ejemplo, si una de las ecuaciones es 4x + 2y = 8, el primer paso es reordenarlo restando 2y de cada lado, así nos queda: 4x = 8 - 2y.
- Por lo general, este método emplea fracciones. Puedes probar el método de eliminación que se explica más adelante si no te gusta utilizar fracciones.
2
Divide ambos lados de la ecuación para “hallar x”. Una vez que tengas el término x (o cualquier otra variable que emplees) en un lado de la ecuación, divide ambos lados para aislar la variable. Por ejemplo:
- 4x = 8 - 2y
- (4x)/4 = (8/4) - (2y/4)
- x = 2 - ½y
3
Reemplázalo nuevamente en la otra ecuación. Asegúrate de hacer lo mismo en la otra ecuación, no en la que ya utilizaste. En esa ecuación, reemplaza la variable que hallaste para que solo quede una. Por ejemplo:
- Sabiendo que x = 2 - ½y,
- La segunda ecuación que aún no has alterado es 5x + 3y = 9.
- En la segunda ecuación, reemplaza x con "2 - ½y": 5(2 - ½y) + 3y = 9.
4
Halla la variable restante. Ahora tienes una ecuación con una sola variable. Utiliza técnicas de álgebra convencionales para hallar dicha variable. Si la variables se cancelan, pasa directamente al último paso. De lo contrario, terminarás con una respuesta para una de las variables:
- 5(2 - ½y) + 3y = 9
- 10 – (5/2)y + 3y = 9
- 10 – (5/2)y + (6/2)y = 9 (si no entiendes este paso, lee el artículo “Cómo sumar fracciones o quebrados”. A veces, aunque no siempre, es necesario para este método).
- 10 + ½y = 9
- ½y = -1
- y = -2
5
Utiliza la respuesta para hallar la otra variable. No cometas el error de dejar el problema a medio terminar. Necesitarás reemplazar la respuesta que obtuviste en una de las ecuaciones originales para que puedas hallar la otra variable:
- Sabiendo que y = -2,
- Una de las ecuaciones originales es 4x + 2y = 8 (puedes utilizar cualquier ecuación para este paso).
- Coloca -2 en lugar de y: 4x + 2(-2) = 8.
- 4x - 4 = 8
- 4x = 12
- x = 3
6
Considera lo que tienes que hacer cuando ambas variables se cancelen. Cuando reemplaces x=3y+2 o una respuesta similar en la otra ecuación, trata de obtener una ecuación con una sola variable. En ocasiones, terminarás con una ecuación sin variables. Verifica tu trabajo y asegúrate de reemplazar (y reordenar) la primera ecuación en la segunda, no solo vuelvas a la primera. Si estás seguro de que no cometiste ningún error, obtendrás uno de los siguientes resultados:^{[1]
X
Fuente de investigación}
- Si terminas con una ecuación que no tiene variables y no es verdadera (por ejemplo, 3 = 5), el problema no tiene solución (si graficas ambas ecuaciones, notarás que son paralelas y que nunca se cruzan).
- Si terminas con una ecuación sin variables que sí es verdadera (como 3 = 3), el problema tiene soluciones infinitas. Ambas ecuaciones son exactamente iguales entre sí (si graficas ambas ecuaciones, notarás que están en la misma línea).
Anuncio

Método 2

Método 2 de 3:
Método de eliminación

1
Halla la variable que se cancela. En ocasiones, las ecuaciones “cancelan” una variable después de sumarlas. Por ejemplo, al combinar 3x + 2y = 11 y 5x - 2y = 13, el "+2y" y el "-2y" se cancelarán entre sí, eliminando a todas las “y” de la ecuación. Observa todas las ecuaciones en el problema y averigua si una de las variables se cancela de esta manera. Si no es posible cancelar ninguna de ellas, lee el siguiente paso para ver más consejos.
2
Multiplica una ecuación para que una variable se cancele (omite este paso si las variables ya se cancelaron). Si las ecuaciones no tienen una variable que se cancela de manera natural, cambia una de ellas para que lo hagan. Será más fácil entenderlo con una imagen:
- Tienes el sistema de ecuaciones 3x - y = 3 y -x + 2y = 4.
- Cambiemos la primera ecuación para que la variable y se cancele (puedes elegir x y obtendrás la misma respuesta al final).
- La - y en la primera ecuación debe cancelarse con el + 2y en la segunda ecuación. Podemos hacerlo al multiplicar - y por 2.
- Multiplica ambos lados de la primera ecuación de la siguiente manera: 2(3x - y)=2(3), de modo que 6x - 2y = 6. Ahora el - 2y se cancelará con el +2y en la segunda ecuación.
3
Combina las dos ecuaciones. Para combinar las dos ecuaciones, suma los lados de la izquierda y los de la derecha. Si formulas bien la ecuación, una de las variables debe cancelarse. Este es un ejemplo que utiliza las mismas ecuaciones como en el paso anterior:
- Las ecuaciones son 6x - 2y = 6 y -x + 2y = 4.
- Combina los lados de la izquierda: 6x - 2y - x + 2y = ?
- Combina los lados de la derecha: 6x - 2y - x + 2y = 6 + 4.
4
Halla la última variable. Simplifica la ecuación combinada y luego utiliza álgebra básica para hallar la última variable. 'Si no quedan variables después de hacer la simplificación, pasa al último paso de esta sección. De lo contrario, debes terminar con una respuesta simple para una de las variables. Por ejemplo:
- Tienes 6x - 2y - x + 2y = 6 + 4.
- Agrupa las variables x e y: 6x - x - 2y + 2y = 6 + 4.
- Simplifica: 5x = 10
- Halla x: (5x)/5 = 10/5, de modo que x = 2.
5
Halla la otra variable. Has hallado una variable, pero aún no has terminado. Reemplaza la respuesta en una de las ecuaciones originales para que puedas hallar la otra variable. Por ejemplo:
- Sabiendo que x = 2 y que una de las ecuaciones originales es 3x - y = 3.
- Reemplaza 2 en lugar de x: 3(2) - y = 3.
- Halla “y” en la ecuación: 6 - y = 3
- 6 - y + y = 3 + y, de modo que 6 = 3 + y
- 3 = y
6
Ten en cuenta lo que debes hacer cuando canceles ambas variables. En ocasiones, combinar las dos ecuaciones dará lugar a una ecuación sin sentido o al menos que no te ayuda a resolver el problema. Verifica la operación desde el principio, pero si no cometiste un error, anota uno de los siguientes casos como tu respuesta:^{[2]
X
Fuente de investigación}
- Si la ecuación combinada no tiene variables y no es verdadera (como 2 = 7), no hay solución que funcione para ambas ecuaciones (si graficas ambas ecuaciones, notarás que son paralelas y nunca se cruzan).
- Si la ecuación combinada no tiene variables y es verdadera (como 0 = 0), existen soluciones infinitas. Las dos ecuaciones no son realmente idénticas (si las graficas, verás que están en la misma línea).
Anuncio

Método 3

Método 3 de 3:
Graficar las ecuaciones

1
Solo utiliza este método cuando te lo soliciten. A menos que utilices una computadora o una calculadora gráfica, solo podrás obtener una respuesta aproximada a múltiples sistemas de ecuaciones mediante este método.^{[3]
X
Fuente de investigación} Tu maestro o tu libro de matemáticas podría solicitarte utilizar este método para que te familiarices con el gráfico de ecuaciones como líneas. También puedes utilizar este método para verificar tus respuestas de uno de los demás métodos.
- La idea básica es graficar ambas ecuaciones y hallar el punto en el que se cruzan. En este punto, los valores de “x” e “y” nos darán sus valores en el sistema de ecuaciones.
2
Resuelve ambas ecuaciones para hallar y. Manteniendo las dos ecuaciones por separado, utiliza tus conocimientos de álgebra para convertir cada ecuación en la forma de “y = __x + __”.^{[4]
X
Fuente de investigación} Por ejemplo:
- La primera ecuación es 2x + y = 5. Cámbiala a y = -2x + 5.
- Tu segunda ecuación es -3x + 6y = 0. Cámbiala a 6y = 3x + 0, luego simplifica a y = ½x + 0.
- Si ambas ecuaciones son idénticas, toda la línea será una “intersección”. Escribe las soluciones infinitas.
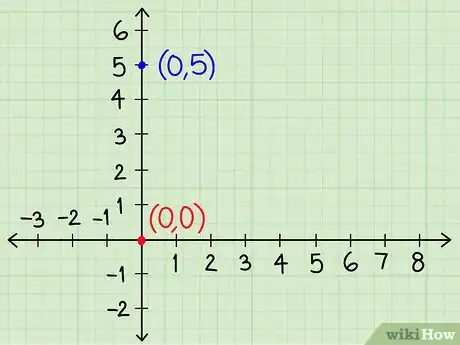
3
Dibuja los ejes de las coordenadas. En una hoja de papel cuadriculada dibuja un “eje y” vertical y un “eje x” horizontal. Comenzando en el punto donde se cruzan, etiqueta los números 1, 2, 3, 4, etc. moviéndote hacia arriba en el eje “y” y hacia la derecha en el eje “x”. Etiqueta los números -1, -2, etc. moviéndote hacia abajo en el eje “y” y hacia la izquierda en el eje “x”.
- Si no tienes papel cuadriculado, utiliza una regla para asegurarte de que los números estén espaciados con precisión.
- Si utilizas número grandes o decimales, es posible que necesites modificar la escala de tu gráfico (por ejemplo: 10, 20, 30 o 0,1; 0,2; 0,3 en lugar de 1, 2, 3).
4
Dibuja la intersección de “y” para cada línea. Una vez que tengas una ecuación en la forma y = __x + __, puedes comenzar a graficarla al dibujar un punto en donde la línea intersecta el eje y. Esta siempre estará en un valor de e igual al último número de esta ecuación.
- En el ejemplo anterior, una línea (y = -2x + 5) intersecta el eje “y” en 5. La otra (y = ½x + 0) intersecta en 0. Estos son los puntos (0,5) y (0,0) en el gráfico.
- Utiliza bolígrafos o lápices de colores diferentes para las dos líneas.
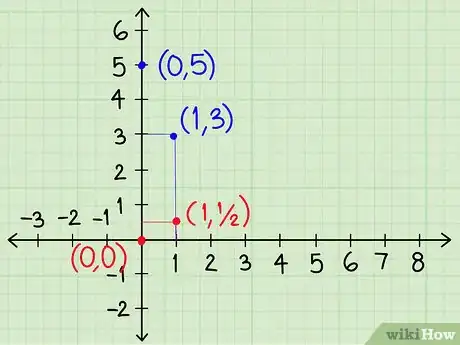
5
Utiliza la pendiente para continuar las líneas. En la forma y = __x + __, el número en frente de la x es la pendiente de la línea. Cada vez que x aumente en uno, el valor de “y” aumentará en la cantidad de la pendiente. Utiliza esta información para trazar el punto en el gráfico para cada línea cuando x = 1 (también puedes reemplazar x = 1 en cada ecuación y hallar el valor de y).
- En nuestro ejemplo, la línea y = -2x + 5 tiene una pendiente de -2. En x = 1, la línea se mueve hacia abajo 2 puntos desde el punto ubicado en x = 0. Dibuja el segmento de línea entre (0,5) y (1,3).
- La línea y = ½x + 0 tiene una pendiente de ½. En x = 1, la línea se mueve hacia arriba ½ punto desde el punto ubicado en x=0. Dibuja el segmento de línea entre (0,0) y (1,½).
- Si las líneas tienen la misma pendiente, nunca se cruzarán, de modo que no hay respuesta para el sistema de ecuaciones. Escribe la frase sin solución.
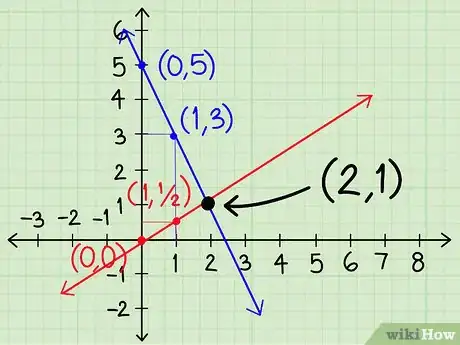
6
Continúa trazando las líneas hasta que se crucen. Detente y mira el gráfico. Si las líneas ya se han cruzado, pasa directamente al siguiente paso. De lo contrario, toma una decisión en base a lo que hacen las líneas:
- Si las líneas se mueven la una hacia la otra, sigue trazando los puntos en esa dirección.
- Si las líneas se alejan la una de la otra, retrocede y traza los puntos en la otra dirección comenzando en x=-1.
- Si las líneas están muy lejos entre sí, trata de trazar puntos más distantes, como en x = 10.
7
Halla la respuesta en la intersección. Una vez que las dos líneas se crucen, los valores de “x” e “y” en ese punto son la respuesta a tu problema. Si tienes suerte, la respuesta será un número entero. Por ejemplo, en nuestros ejemplos, las dos líneas se cruzan en (2,1) así que la respuesta es x = 2 e y = 1. En algunos sistemas de ecuaciones, las líneas se cruzarán en un valor ubicado entre dos números enteros y, a menos que tu gráfico sea extremadamente preciso, será más difícil determinar dónde se encuentra esta intersección. Si esto sucede, puedes escribir una respuesta como "x se encuentra entre 1 y 2" o utiliza el método de sustitución o eliminación para hallar la respuesta exacta.

Anuncio

Consejos

Puedes verificar tu trabajo al reemplazar las respuestas en las ecuaciones originales. Si las ecuaciones son verdaderas (por ejemplo, 3 = 3), tu respuesta es correcta.
En el método de eliminación, generalmente tendrás que multiplicar por un número negativo con la finalidad de tener una variable que puedas cancelar.

Anuncio

Advertencias

No es posible utilizar estos métodos si existe una variable elevada a un exponente como x². Para obtener más información en lo relacionado a ecuaciones de este tipo, busca una guía que te ayude a factorizar ecuaciones cuadráticas con dos variables.^{[5]
X
Fuente de investigación}

Anuncio