Cómo utilizar una regla de cálculo

Para alguien que no sabe cómo usarla, una regla de cálculo puede parecer un diseño de Picasso. Existen por lo menos tres escalas diferentes y en la mayoría de ellas los números no están separados a una distancia uniforme. Sin embargo, después de aprender a usarla, podrás ver la razón por la que esta regla era tan útil en los siglos anteriores a la invención de las calculadoras de bolsillo. Alinea los números correctos en la escala y podrás multiplicar cualquier número con una matemática mucho más simple que la que usarías con un lápiz y papel.

Parte 1
Parte 1 de 4:
Entender las reglas de cálculo

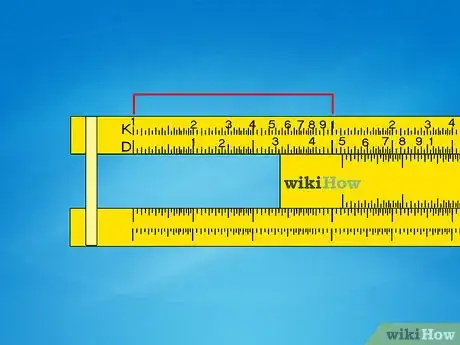
  1. Imagen titulada Use a Slide Rule Step 1
    1
    Observa los espacios entre los números. A diferencia de una regla común, los números en una regla de cálculo no están separados en una escala uniforme y lineal. En lugar de eso, están separados mediante una fórmula “logarítmica” especial, estando más cerca en un lado que en el otro. Esto te permitirá alinear las escalas para obtener la respuesta a los problemas de multiplicación, tal como se describe más adelante.
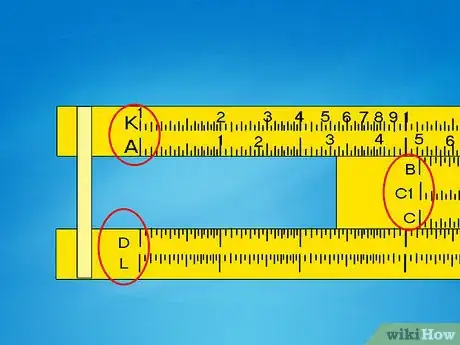
  2. Imagen titulada Use a Slide Rule Step 2
    2
    Busca las etiquetas para las escalas. Cada escala en la regla de cálculo debe tener una letra o símbolo que la identifique impreso a la izquierda o a la derecha. Esta guía asumirá que tu regla de cálculo utiliza la notación más común:[1]
    • Las escalas C y D se parecen a una sola regla extendida y se leen de izquierda a derecha. A estas escalas se les conoce como escalas de “una decena”.
    • Las escalas A y B son escalas de “dos decenas”. Cada una tiene reglas extendidas más pequeñas que se apilan de un extremo al otro.
    • La escala K es una escala de tres decenas o una serie de tres reglas extendidas y apiladas de un extremo a otro. No todos los modelos cuentan con esta escala.
    • Las escalas C| y D| son las mismas que las C y D, pero se leen de derecha a izquierda. Por lo general, están impresas en color rojo. No todos los modelos cuentan con estas escalas.
  3. Imagen titulada Use a Slide Rule Step 3
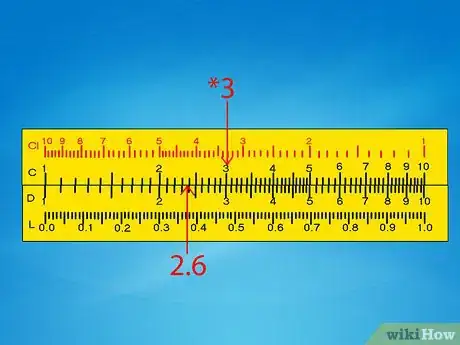
    3
    Interpreta las divisiones de la escala. Observa las líneas verticales de la escala C o D y acostúmbrate a leerlas:
    • Los números primarios en la escala comienzan con el 1 en el extremo izquierdo, extendiéndose hasta el 9, para luego terminar con otro 1 en el extremo derecho. Por lo general, todos estos números están etiquetados.
    • Las divisiones secundarias, marcadas con las segundas líneas verticales más grande, dividen cada número primario en 0,1. No te confundas si están etiquetadas como “1, 2, 3”; recuerda que en realidad representan “1,2, 1,2, 1,3” y así sucesivamente.
    • Por lo general, hay divisiones más pequeñas que normalmente representan aumentos de 0,02. Presta mucha atención, ya que podrían desaparecer en el extremo superior de la escala, donde los números se acercan más.
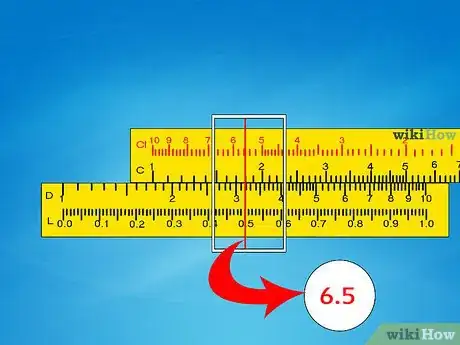
  4. Imagen titulada Use a Slide Rule Step 4
    4
    No esperes obtener respuestas exactas. Al momento de leer una escala, generalmente tendrás que hacer una “mejor estimación” cuando la respuesta no quede exactamente en una línea. Las reglas de cálculo sirven para realizar cálculos rápidos y no para situaciones en las que se requiere una precisión extrema.
    • Por ejemplo, si la respuesta se encuentra entre las marcas 6,51 y 6,52, anota el valor más cercano. Si no puedes determinarlo, escribe 6,515.

Parte 2
Parte 2 de 4:
Multiplicar números

  1. Imagen titulada Use a Slide Rule Step 5
    1
    Anota los números que vas a multiplicar. Anota los dos números que planeas multiplicar.
    • En el ejemplo1 de esta sección, calcularemos 260 x 0,3.
    • En el ejemplo 2, calcularemos 410 x 9. Esto terminará siendo un poco más complicado que en el ejemplo 1, así que es posible que quieras seguir el ejemplo 1 primero.
  2. Imagen titulada Use a Slide Rule Step 6
    2
    Mueve las comas decimales para cada número. La regla de cálculo solo está etiquetada con números entre el 1 y el 10. Mueve la coma decimal en cada número que vayas a multiplicar, de modo que se encuentren entre estos valores. Después de completar el problema, moveremos la coma decimal en la respuesta de vuelta al lugar correcto, tal como se describe al final de esta sección.
    • Ejemplo 1: para calcular 260 x 0,3 en una regla de cálculo, comienza con 2,6 x 3.
    • Ejemplo 2: para calcular 410 x 9, comienza con 4,1 x 9.
  3. Imagen titulada Use a Slide Rule Step 7
    3
    Halla el número más pequeño en la escala D y luego desliza la escala C hacia él. Halla el número más pequeño en la escala D. Luego desliza la escala C de modo que el “1” en el extremo izquierdo (también llamado índice izquierdo) esté alineado directamente con dicho número.
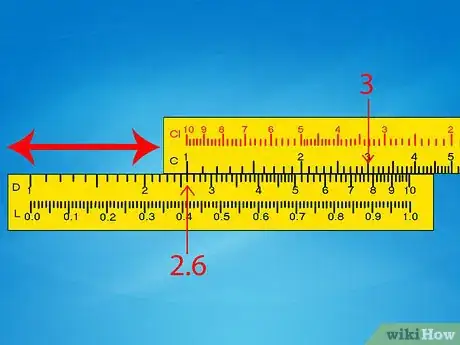
    • Ejemplo 1: desliza la escala C de modo que el índice izquierdo esté alineado con el 2,6 en la escala D.
    • Ejemplo 2: desliza la escala C de modo que el índice izquierdo esté alineado con el 4,1 en la escala D.
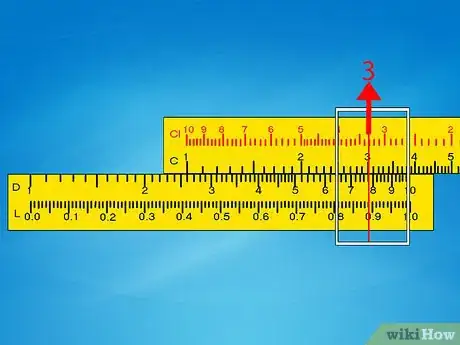
  4. Imagen titulada Use a Slide Rule Step 8
    4
    Desliza el cursor de metal hacia el segundo número en la escala C. El cursor es el objeto metálico que se desliza sobre toda la regla de cálculo. Alinéalo con el segundo número en el problema de multiplicación, en la escala C. El cursor apuntará la respuesta al problema en la escala D. Si no puedes deslizarlo tan lejos, ve al siguiente paso.
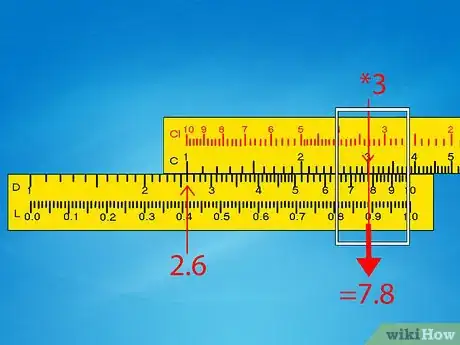
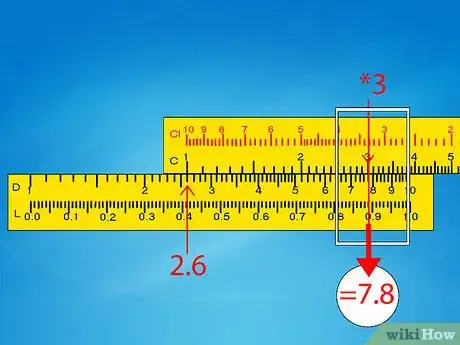
    • Ejemplo 1: desliza el cursor para que apunte al 3 en la escala C. En esta posición, también debe apuntar al 7,8 en la escala D o estará muy cerca de él. Ve directamente al paso 6 de esta sección.
    • Ejemplo 2: intenta desliza el cursor de modo que apunte al 9 en la escala C. en la mayoría de las reglas de cálculo, esto no es posible o el cursor apuntará a un espacio vacío fuera del extremo de la escala D. Lee el siguiente paso para ver cómo solucionarlo.
  5. Imagen titulada Use a Slide Rule Step 9
    5
    Utiliza el índice derecho en caso de que el cursor no se deslice hacia la respuesta. Si el cursor está bloqueado debido a un “puente” en el centro de la regla de cálculo o si la respuesta está “fuera de la escala”, emplea un método ligeramente distinto.[2] Desliza la escala C de modo que el “índice derecho” o el número 1 en el extremo derecho se encuentre sobre el factor más grande en el problema de multiplicación. Desliza el cursor hacia la ubicación del otro factor en la escala C y lee la pregunta en la escala D.
    • Ejemplo 2: desliza la escala C de modo que el número 1 en el extremo derecho se alinee con el 9 en la escala D. Desliza el cursor hacia el 4,1 en la escala C. El cursor apuntará a la escala D entre el 3,68 y el 3,7 de modo que la respuesta debe ser aproximadamente 3,69.
  6. Imagen titulada Use a Slide Rule Step 10
    6
    Utiliza la estimación para hallar la coma decimal correcta. Independientemente de la multiplicación que realices, la respuesta siempre se leerá en la escala D, lo que solo mostrará los números del 1 al 10. Necesitarás realizar una estimación y cálculo mental para determinar el lugar donde colocar la coma decimal en la respuesta.
    • Ejemplo 1: nuestro problema original era 260 x 0,3 y la regla de cálculo nos dio una respuesta de 7,8. Redondea el problema original hacia los números convenientes y resuélvelo en tu mente: 250 x 0,5 = 125. Esto está mucho más cerca de 78 que de 780 o 7,8, así que la respuesta será 78.
    • Ejemplo 2: nuestro problema original era 410 x 9 y obtuvimos una respuesta de 3,69 en la regla de cálculo. Calcula el problema original como 400 x 10 = 4,000. El resultado más cercano que podemos obtener al mover la coma decimal es 3,690, así que esa debe ser la respuesta real.

Parte 3
Parte 3 de 4:
Hallar cuadrados y cubos

  1. Imagen titulada Use a Slide Rule Step 11
    1
    Utiliza las escalas D y A para hallar los cuadrados. Por lo general, estas dos escalas están fijas en su lugar. Simplemente desliza el cursor de metal hacia un valor en la escala D y el valor A será su cuadrado.[3] Al igual que un problema de multiplicación, necesitarás determinar la posición de la coma decimal por tu cuenta.
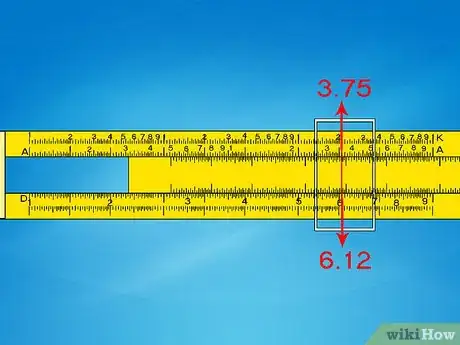
    • Por ejemplo, para resolver 6,12, desliza el cursor a 6,1 en la escala D. el valor correspondiente A es de aproximadamente 3,75.
    • Calcula 6.12 a 6 x 6 = 36. Coloca la coma decimal para obtener una respuesta cercana a este valor: 37,5.
    • Ten en cuenta que la respuesta exacta es 37,21. La respuesta con la regla de cálculo varía en menos de 1 %, un valor lo suficientemente preciso para la mayoría de las circunstancias del mundo real.
  2. Imagen titulada Use a Slide Rule Step 12
    2
    Utiliza las escalas D y K para hallar los cubos. Acabas de ver cómo la escala A, la cual es una escala D reducida a la mitad, te permite hallar el cuadrado de los números. Del mismo modo, la escala K, la cual es una escala D reducida a un tercio de escala, te permite hallar los cubos. Simplemente desliza el cursor hacia un valor D y lee el resultado en la escala K. Realiza una estimación para colocar la coma decimal.
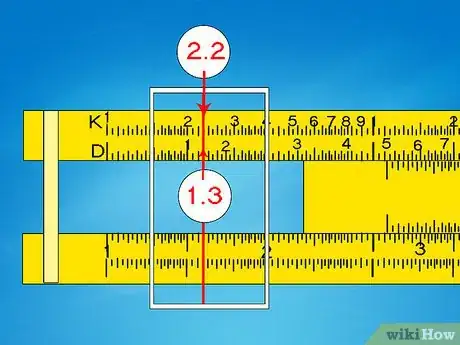
    • Por ejemplo, para resolver 1303, desliza el cursor hacia 1,3 en el valor D. el valor K correspondiente será 2,2. Dado que 1003 = 1 x 106 y que 2003 = 8 x 106, sabemos que la respuesta debe situarse en algún punto entre dichos números. Por lo tanto, la respuesta debe ser 2,2 x 106 o 2,200,000.

Parte 4
Parte 4 de 4:
Hallar raíces cuadradas y raíces cúbicas

  1. Imagen titulada Use a Slide Rule Step 13
    1
    Convierte el número a una notación científica antes de hallar una raíz cuadrada. Como siempre, la regla de cálculo solo tiene valores que van del 1 al 10, así que necesitarás escribir el número en una notación científica antes de poder hallar su raíz cuadrada.
    • Ejemplo 3: para resolver √(390), escríbelo como √(3,9 x 102).
    • Ejemplo 4: para resolver √(7100), escríbelo como √(7,1 x 103).
  2. Imagen titulada Use a Slide Rule Step 14
    2
    Determina qué lado de la escala A utilizarás. Para hallar la raíz cuadrada de un número, el primer paso es deslizar el cursor para que ese número esté en la escala A. Sin embargo, debido a que la escala A está impresa dos veces, deberás decidir cuál utilizarás primero.[4] Para hacerlo, sigue las siguientes reglas:
    • Si el exponente en la notación científica es par (como 2 en el ejemplo 3), utiliza el lado izquierdo de la escala A (la “primera decena”).
    • Si el exponente en la notación científica es impar, (como 3 en el ejemplo 4), utiliza el lado derecho de la escala A (la “segunda decena”).
  3. Imagen titulada Use a Slide Rule Step 15
    3
    Desliza el cursor en la escala A. Ignora el exponente de las decenas por ahora y desliza el cursor de metal a lo largo de la escala A hasta el número con el que terminaste.
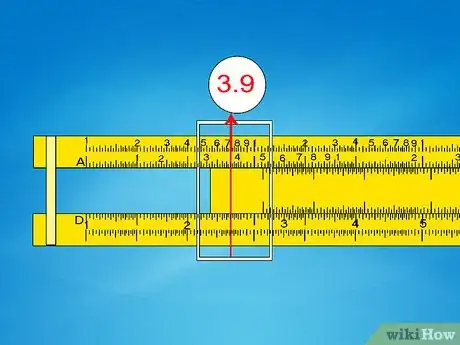
    • Ejemplo 3: para hallar √(3,9 x 102), desliza el cursor hasta 3,9 en la escala A de la izquierda (utiliza la escala izquierda porque el exponente es par, tal como se describe anteriormente).
    • Ejemplo 4: para hallar √(7,1 x 103), desliza el cursor hasta 7,1 en la escala A de la derecha (utiliza la escala derecha porque el exponente es impar).
  4. Imagen titulada Use a Slide Rule Step 16
    4
    Determina la respuesta desde la escala D. Lee el valor D donde apunta el cursor. Agrega “x10n” a este valor. Para calcular n, toma la potencia de 10 original, redondea al número par más cercano y luego divide entre 2.
    • Ejemplo 3: el valor D correspondiente en A=3,9 es aproximadamente 1,975. El número original en la notación científica tenía 102. 2 es un número par, así que divide entre 2 para obtener 1. La respuesta final será 1,975 x 101 = 19,75.
    • Ejemplo 4: el valor D correspondiente en A=7,1 es aproximadamente 8,45. El número original en la notación científica tenía 103, así que redondea el 3 al número par más cercano, 2, luego divide entre 2 para obtener 1. La respuesta final será 8,45 x 101 = 84,5.
  5. Imagen titulada Use a Slide Rule Step 17
    5
    Utiliza un proceso similar en la escala K para hallar las raíces cúbicas. El proceso para hallar las raíces cúbicas es muy similar. El paso más importante es determinar cuál de las tres escalas K utilizar. Para ello, divide la cantidad de dígitos en el número entre tres y halla el residuo. Si el residuo es 1, utiliza la primera escala; si es 2, utiliza la segunda y si es 3, utiliza la tercera. Otra forma de hacerlo es contar repetidas veces desde la primera escala hacia la tercera hasta llegar al número de dígitos que hay en la respuesta.[5]
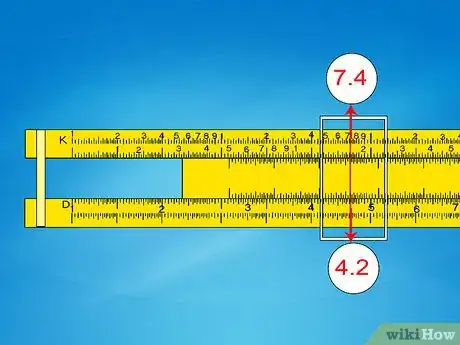
    • Ejemplo 5: para hallar la raíz cúbica de 74,000, primero cuenta la cantidad de dígitos (5), divide entre 3 y halla el residuo (1 con residuo 2). Dado que el residuo es 2, emplea la segunda escala (también puedes contar las escalas cinco veces: 1–2–3–1–2).
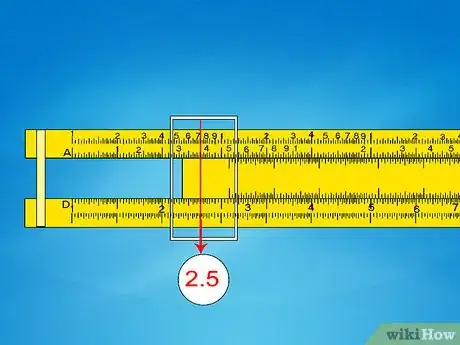
    • Desliza el cursor hacia 7,4 en la segunda escala K. El valor D correspondiente será de aproximadamente 4,2.
    • Dado que 103 es más menor que 74,000, pero 1003 es mayor que 74,000, la respuesta debe encontrarse entre 10 y 100. Mueve la coma decimal para formar el 42.

Consejos

  • Hay otras funciones que puedes calcular en la regla de cálculo, sobre todo si contiene escalas “log-log”, escalas para cálculos trigonométricos u otras escalas especializadas. Practica con ellas o busca en Internet la letra al lado de la escala para obtener más información.
  • Puedes utilizar el método de la multiplicación para realizar conversiones entre dos unidades de medida. Por ejemplo, dado que 1 pulgada = 2,54 centímetros, el problema “convertir 5 pulgadas a centímetros” puede considerarse el siguiente problema de multiplicación: 5 x 2.54.
  • La exactitud de una regla de cálculo depende de la cantidad de marcas de calibración distinguibles puedes hacer en ella. Mientras más larga sea la regla, más precisa puede ser.

Advertencias

  • Mantén tu regla de cálculo alejada del calor y la humedad, pues la deformación y el encogimiento puede hacer que pierda su exactitud.[6]

wikiHows relacionados

calcular el diámetro de un círculo
Cómo
calcular el diámetro de un círculo
calcular un incremento en porcentaje
Cómo
calcular un incremento en porcentaje
calcular la variación porcentual
Cómo
calcular la variación porcentual
encontrar el valor de X
Cómo
encontrar el valor de X
medir milímetros
Cómo
medir milímetros
calcular una frecuencia
Cómo
calcular una frecuencia
calcular las probabilidades de sacarte la lotería
Cómo
calcular las probabilidades de sacarte la lotería
convertir de grados a radianes
Cómo
convertir de grados a radianes
calcular la incertidumbre
Cómo
calcular la incertidumbre
calcular la varianza
Cómo
calcular la varianza
convertir radianes a grados
Cómo
convertir radianes a grados
calcular la velocidad
Cómo
calcular la velocidad
calcular el porcentaje de error
Cómo
calcular el porcentaje de error
encontrar una raíz cuadrada sin una calculadora
Cómo
encontrar una raíz cuadrada sin una calculadora

Referencias

  1. ↑ http://sliderulemuseum.com/SR_Course.htm
  2. ↑ http://sliderulemuseum.com/SR_Course.htm
  3. ↑ http://www.sliderules.info/a-to-z/tys/tys03.htm# A%20and%20B%20Scales
  4. ↑ http://www.sliderules.info/a-to-z/tys/tys03.htm# A%20and%20B%20Scales
  5. ↑ http://www.antiquark.com/sliderule/sim/sr-calcs-by-example.html# mozTocId734623
  6. ↑ http://www.sliderules.info/a-to-z/tys/tys03.htm

Acerca de este wikiHow

wikiHow es un "wiki", lo que significa que muchos de nuestros artículos están escritos por varios autores. Para crear este artículo, 10 personas, algunas anónimas, han trabajado para editarlo y mejorarlo con el tiempo. Este artículo ha sido visto 17 263 veces.
Categorías: Matemáticas