Cet article a été rédigé avec la collaboration de nos éditeurs(trices) et chercheurs(euses) qualifiés(es) pour garantir l'exactitude et l'exhaustivité du contenu.
L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité.
Cet article a été consulté 29 883 fois.
Élever une fraction au carré est l'une des opérations les plus faciles à faire avec les fractions. Cette opération est très similaire au fait de mettre au carré n'importe quel nombre entier, dans la mesure où cela revient à élever au carré le numérateur puis le dénominateur. Il y a également des cas où il est préférable de simplifier la fraction avant de la mettre au carré pour faciliter davantage l'opération. Si vous n'avez pas encore appris à élever une fraction au carré, sachez qu'il existe des méthodes toutes simples qui vous aideront à comprendre plus rapidement ce calcul algébrique.
Étapes
Partie 1
Partie 1 sur 3:Mettre au carré des fractions
-
1Apprenez à mettre au carré des nombres entiers. La puissance 2 d'un nombre revient à mettre au carré le nombre en question. Pour ce faire, vous devez multiplier ce nombre deux fois par lui-même [1] . Voici un exemple :
- 52 = 5 × 5 = 25
-
2Comprenez que l'élévation au carré des fractions suit le même principe. Pour ce faire, il faut multiplier la fraction par elle-même. En d'autres termes, il faut multiplier le numérateur par lui-même et en faire de même avec le dénominateur. Voici un exemple :
- (5/2)2 = 5/2 × 5/2 ou (52/22)
- Élevez au carré chaque nombre que vous obtenez : (25/4)
-
3Mettez au carré le numérateur, puis le dénominateur. L'ordre d'effectuer ces multiplications importe peu, aussi longtemps que vous les mettez tous au carré. Pour faciliter les choses, commencez par le numérateur : il suffit de le multiplier par lui-même. Puis, faites la même chose avec le dénominateur.
- Le numérateur est le nombre placé au-dessus de la barre horizontale de la fraction et le dénominateur reste en dessous de cette barre.
- Voici un exemple : (5/2)2 = (5 x 5/2 x 2) = (25/4)
-
4Pour finir, simplifiez la fraction. Lorsque vous faites des exercices avec des fractions, vous devez toujours réduire la fraction à sa forme la plus simple ou à transformer une fraction impropre en nombre mixte [2] . Dans l'exemple utilisé, 25/4 est une fraction impropre parce que le numérateur est supérieur au dénominateur.
- Pour le convertir en un nombre mixte, divisez 25 par 4. Le nombre 25 est encore égal à 6 (6 x 4 = 24) plus 1. Par conséquent, le nombre mixte est 6 1/4
Publicité
Partie 2
Partie 2 sur 3:Élever au carré des fractions avec des nombres négatifs
-
1Reconnaissez le signe négatif dans une fraction. Pour reconnaitre une fraction négative, recherchez le signe moins devant cette dernière. Il est conseillé de placer toujours les nombres négatifs entre parenthèses. Ainsi, vous serez que le signe « - » se réfère au nombre et qu'il ne doit pas être considéré comme un signe de soustraction [3] .
- Voici un exemple : (–2/4)
-
2Multipliez la fraction par elle-même. Élever la fraction au carré comme vous le feriez normalement, en multipliant le dénominateur par lui-même et le numérateur par lui-même. Si vous préférez, vous pouvez simplement multiplier la fraction par elle-même.
- Voici un exemple : (–2/4)2 = (–2/4) x (–2/4)
-
3Sachez que multiplier 2 nombres négatifs donne un nombre positif. Quand il y a un signe moins dans une fraction, toute la fraction est négative. Lorsque vous mettez cette dernière au carré, cela revient à multiplier ensemble deux nombres négatifs, ce qui donnera une valeur positive [4] .
- Voici un exemple : (-2) x (-8) = (+16)
-
4Retirez le signe moins après l'opération. Après avoir mis une fraction au carré, vous obtiendrez deux nombres négatifs multipliés entre eux. Cela signifie que la fraction élevée au carré sera un nombre positif. N'oubliez pas d'écrire la réponse finale sans le signe moins.
- En reprenant notre exemple, le résultat de la fraction sera un nombre positif
- (–2/4) x (–2/4) = (+4/16)
- En général, on omet le signe « + » devant les nombres positifs [5] .
-
5Réduisez la fraction sous sa forme la plus simple. Pour ces calculs algébriques, la dernière étape est de toujours simplifier la fraction. Les fractions impropres doivent être simplifiées en des nombres mixtes, puis être réduites.
- Par exemple, (4/16) a un facteur commun, qui est le chiffre quatre.
- Divisez la fraction par 4 : 4/4 = 1, 16/4= 4
- Quand on réécrit la fraction sous sa forme simplifiée, on obtient (1/4)
Publicité
Partie 3
Partie 3 sur 3:Utiliser les simplifications et des raccourcis
-
1Voyez si vous pouvez simplifier la fraction avant de l'élever au carré. En général, il est plus facile de réduire une fraction avant de la mettre au carré. N'oubliez pas ceci : réduire une fraction revient à la diviser par un facteur commun, jusqu'à ce qu'elle soit irréductible [6] . Tout d'abord, réduire une fraction signifie que vous n'êtes pas tenu de le faire à la fin lorsque les nombres sont plus élevés.
- Prenons cet exemple : (12/16)2
- 12 et 16 sont divisibles par 4. 12/4 = 3 et 16/4 = 4. Par conséquent, 12/16 peut être réduit à 3/4
- Maintenant, nous allons mettre 3/4 au carré.
- (3/4)2 = 9/16, qui ne peut être réduit davantage.
- Pour vérifier ce résultat, élevons notre première fraction au carré, sans la réduire :
- (12/16)2 = (12 x 12/16 x 16) = (144/256)
- (144/256) a un facteur commun égal à 16. Divisons le numérateur et le dénominateur par 16. On obtient comme fraction (9/16), qui n'est rien d'autre que la même fraction obtenue précédemment par réduction.
-
2Reconnaissez les cas où il est préférable d'attendre avant la simplification. Lorsque vous avez affaire à des équations plus complexes, vous pouvez tout simplement annuler l'un des facteurs. Dans ce cas, il est efficacement plus facile d'attendre avant de réduire la fraction. Illustrons cette situation en ajoutant un facteur supplémentaire à l'exemple ci-dessus.
- Par exemple : 16 × (12/16)2
- Développez le carré et rayez le facteur commun de 16 :
16*12/16*12/16- Étant donné qu'il n'y a qu'un seul nombre entier 16, qui se retrouve deux fois au dénominateur, vous pouvez en faire disparaitre un.
- Réécrivez l'équation simplifiée : 12 × 12/16
- Réduisez la fraction 12/16 en la divisant par 4 : 3/4
- Multipliez : 12 × 3/4 = 36/4
- Divisez : 36/4 = 9
-
3Apprenez à utiliser les exposants. Une autre façon de résoudre ces opérations consiste à simplifier d'abord l'exposant. Le résultat final est le même, c'est juste la procédure qui diffère.
- Par exemple : 16*(12/16)2
- Réécrivez la fraction en mettant le numérateur et le dénominateur au carré : 16*(122/162)
- Faites disparaitre l'exposant au dénominateur :
16*122/162- Imaginez que le premier 16 a pour exposant le chiffre 1 : 161. En utilisant la règle de calcul des puissances, vous allez soustraire les exposants. 161/162, ce qui donne 161-2 = 16-1 ou 1/16
- À présent, vous allez continuer avec cette fraction : 122/16
- Essayez de la réécrire et de la réduire : 12*12/16 = 12*3/4
- Multipliez : 12 × 3/4 = 36/4
- Divisez : 36/4 = 9
Publicité
Éléments nécessaires
- Une feuille ou un ordinateur pour faire les calculs
- Un crayon ou un bic
Références
- ↑ http://www.math.com/school/subject1/lessons/S1U1L9DP.html
- ↑ https://www.mathsisfun.com/improper-fractions.html
- ↑ https://www.mathsisfun.com/multiplying-negatives.html
- ↑ https://www.mathsisfun.com/multiplying-negatives.html
- ↑ https://www.mathsisfun.com/multiplying-negatives.html
- ↑ http://www.math.com/school/subject1/lessons/S1U4L2GL.html
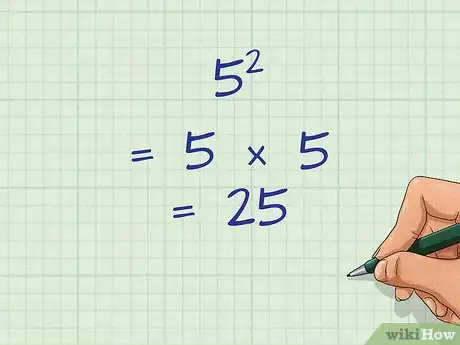
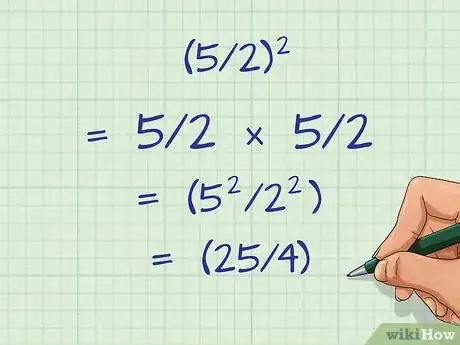
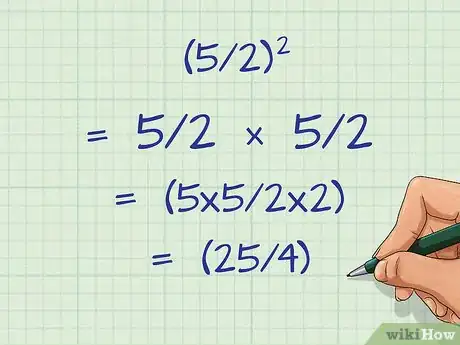
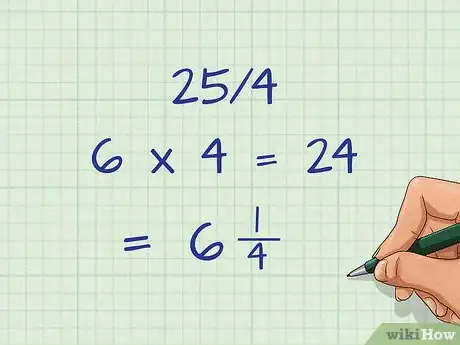
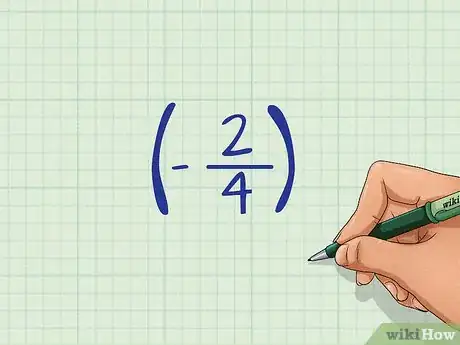
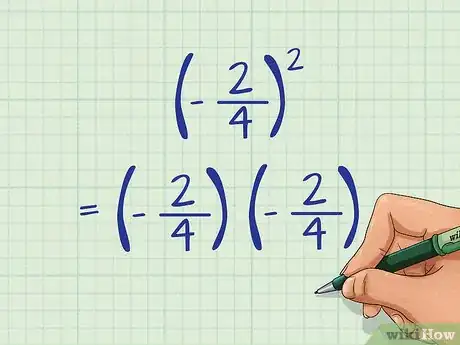
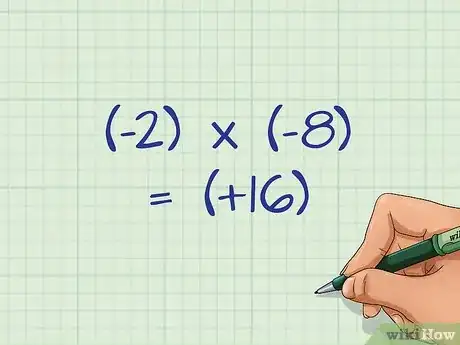
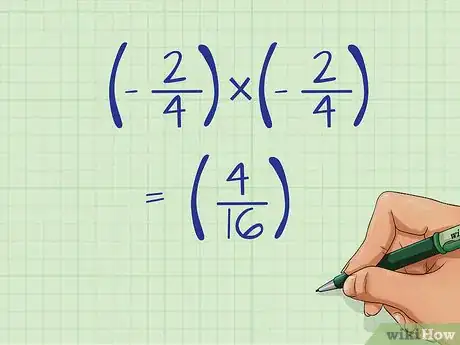
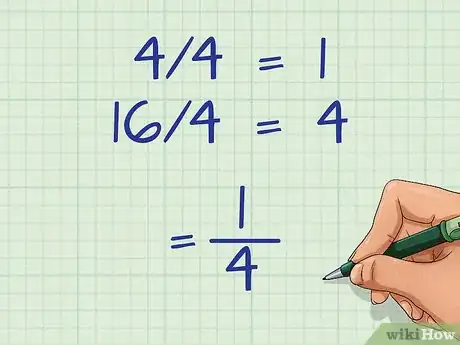
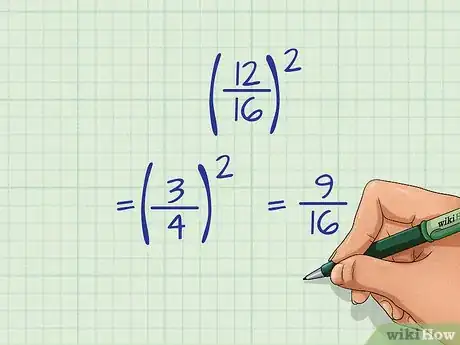

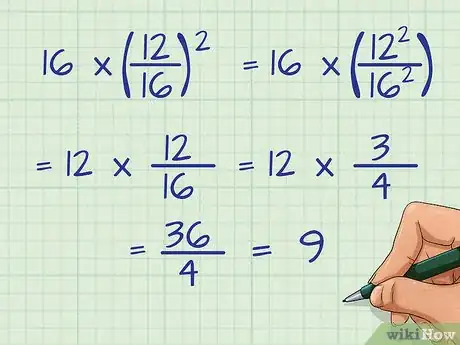



















L'équipe de gestion du contenu de wikiHow examine soigneusement le travail de l'équipe éditoriale afin de s'assurer que chaque article est en conformité avec nos standards de haute qualité. Cet article a été consulté 29 883 fois.