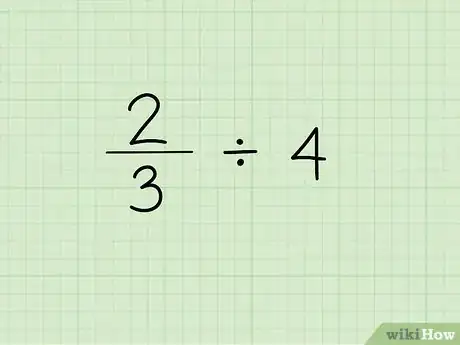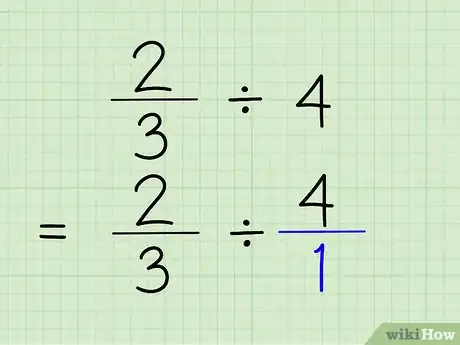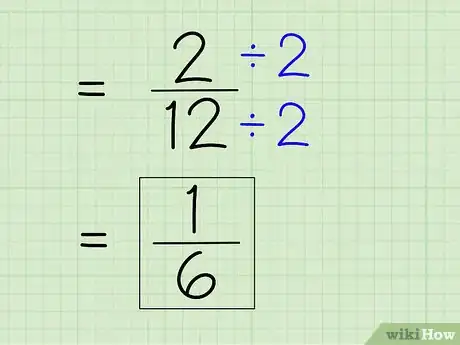Comment diviser une fraction par un nombre entier

Informations concernant l'auteur.e

Diviser une fraction par un entier est finalement assez simple. Il faut d’abord transformer l’entier en fraction, ensuite de quoi on prend l’inverse de cette fraction et on multiplie par la première fraction. La division s’est transformée en multiplication !

Méthode 1

Méthode 1 sur 1:
Diviser une fraction par un nombre entier

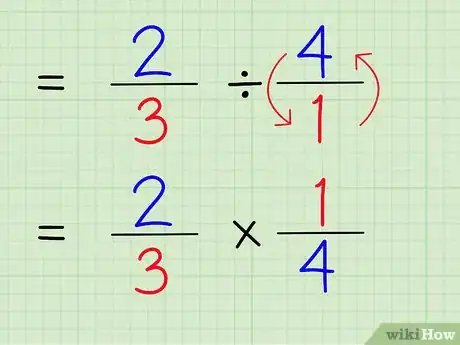
1
Écrivez l’opération sur le papier. C’est la première étape : mettez la fraction, puis le signe de la division et enfin l’entier diviseur. Soyons concret ! on prendra l’opération suivante : 2/3 ÷ 4^{[1]
X
Source de recherche}.
2
Transformez l’entier en fraction. C’est simple, il suffit de le mettre sur 1. Votre entier est devenu le numérateur et 1 est le dénominateur. Les deux expressions 4/1 et 4 sont identiques. Le problème se présente alors ainsi : 2/3 ÷ 4/1.
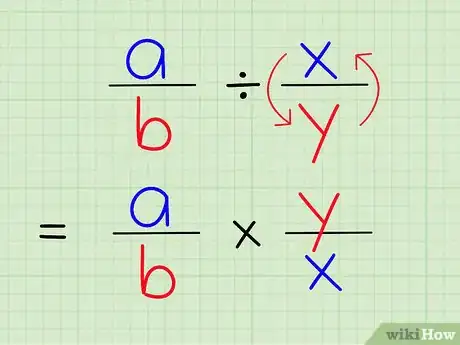
3
Diviser deux fractions consiste à multiplier la première par l’inverse de la seconde.
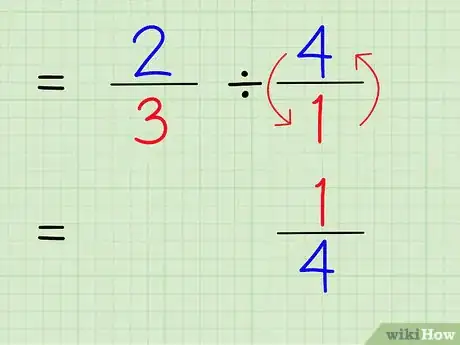
4
Notez l’inverse de la fraction issue de l’entier. Pour trouver l’inverse d’une fraction, il faut intervertir le numérateur et le dénominateur. L’inverse de 4/1 est 1/4.
5
Remplacez le signe de division par un signe de multiplication. Le problème se présente alors ainsi : 2/3 x 1/4.
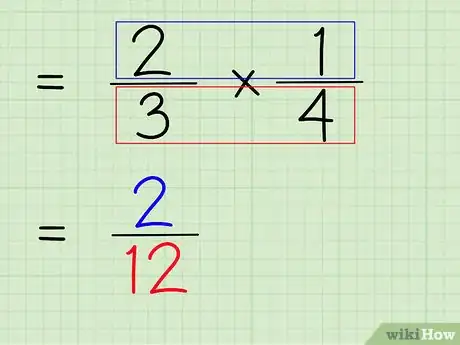
6
Multipliez les numérateurs entre eux, et pareil pour les dénominateurs. Le numérateur final est le produit des deux numérateurs, et le dénominateur final est le produit des deux dénominateurs.
- Ici multipliez 2 par 1, ça fait 2.
- Puis multipliez les dénominateurs : 3 x 4 =12.
- 2/3 x 1/4 = 2/12
7
Réduisez la fraction à sa plus simple expression. Pour simplifier, il faut trouver le plus grand commun diviseur (PGCD) des deux termes, et divisez ces derniers par ce PGCD. 2 étant en numérateur, regardez si le dénominateur est pair. C’est le cas ! Donc, divisez le numérateur et le dénominateur par 2.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- La fraction 2/12 peut se réduire à 1/6. C’est votre réponse définitive.
Publicité

Conseils

Voici une phrase mnémotechnique pour retenir le principe : “Pour diviser une fraction, je ne me complique pas la vie, j’inverse le deuxième nombre et je multiplie !” À vous de voir si ça peut vous être utile !
Une variante de la méthode ci-dessus est la formule GCI/GIC. Gardez le premier nombre. Changez en multiplication. Inversez le dernier nombre. Ou I avant C.
Si vous simplifiez avant de multiplier, vous n’aurez probablement pas besoin de trouver le plus petit dénominateur commun à la fin, car les fractions seront déjà sous leur plus simple expression. Dans notre exemple, avant de multiplier 2/3 x 1/4, on peut remarquer que le premier numérateur (2) et le second dénominateur (4) ont un facteur commun : 2, et peuvent être simplifiés à l’avance. Cela ramène le problème à l’énoncé suivant 1/3 x 1/2, nous donnant immédiatement 1/6 comme résultat et nous évitant d’avoir à réduire la fraction à sa plus simple expression à la fin.
Cette méthode est valable pour les fractions négatives. Il suffit juste de bien garder en tête qu’il y a une valeur négative.

Avertissements

On ne prend l’inverse que de la seconde fraction, celle par laquelle on divise. Dans notre exemple, nous avons converti 4/1 en 1/4, mais nous avons laissé 2/3 telle quelle (nous ne l’avons pas inversée en 3/2).