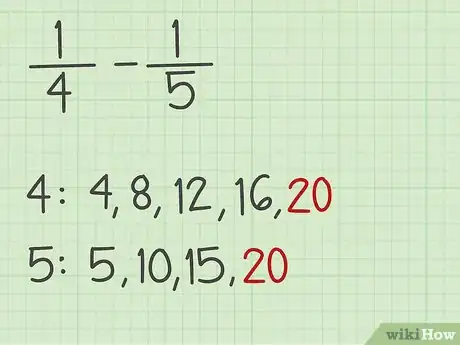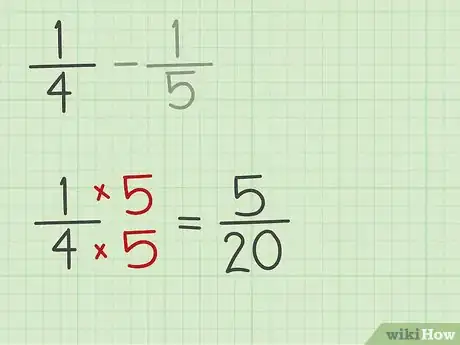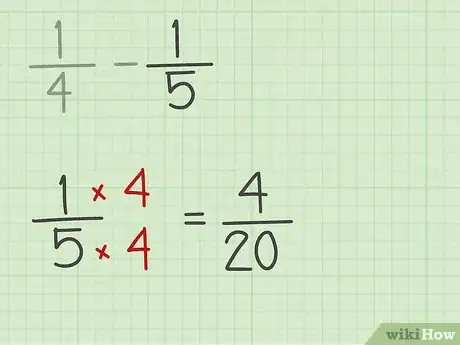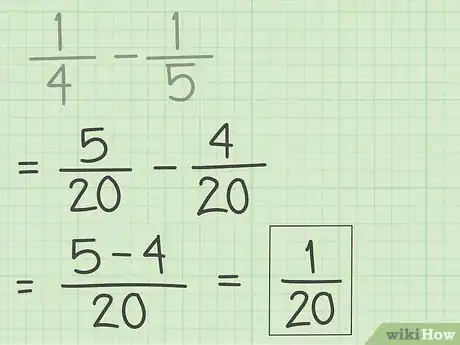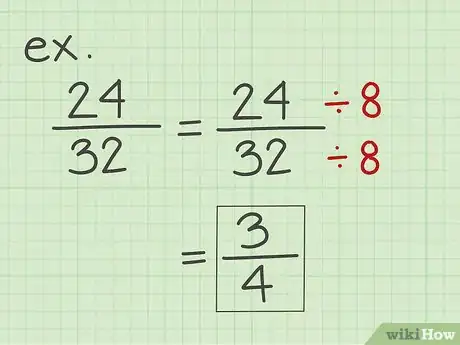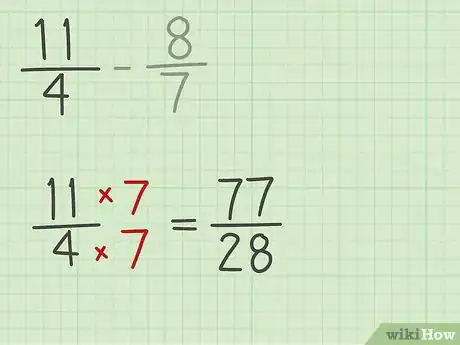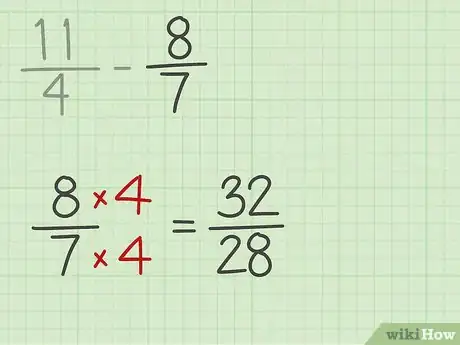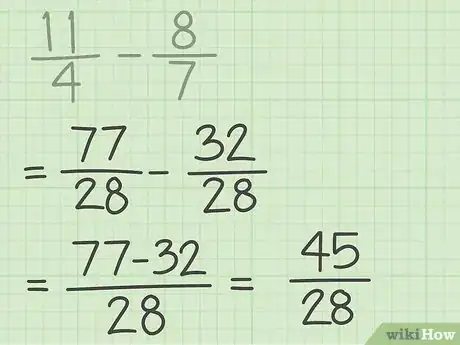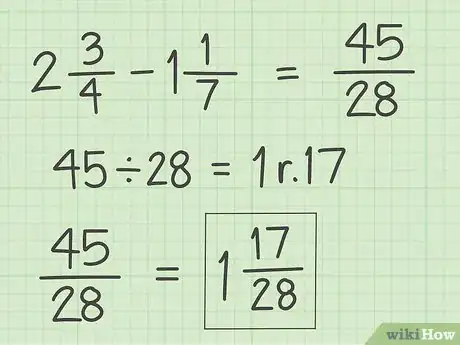Comment soustraire des fractions

Coécrit par David Jia

Soustraire des fractions n’est pas une opération aussi complexe qu’il y parait. Comme pour l’addition, il suffit de trouver un dénominateur commun entre les termes de l’opération. Maitrisez cette règle de base et la manipulation de fractions deviendra un jeu d’enfant !

Méthode 1

Méthode 1 sur 2:
Soustraire des fractions simples

1
Cherchez un dénominateur commun. Il n’est pas possible de soustraire ou d’additionner des fractions dont le dénominateur est différent. Pour réaliser l’opération, il faut donc réécrire les fractions de sorte que ce nombre soit le même. L’une des solutions est de lister tous les multiples des dénominateurs jusqu’à trouver un nombre commun ^{[1]
X
Source de recherche}. Ce nombre, qui est le plus petit entier positif à la fois multiple des deux dénominateurs, est appelé le plus petit commun multiple ou PPCM ^{[2]
X
Source de recherche}.
- Par exemple, supposons que l’opération soit 1/4 – 1/5. Les multiples de 4 sont 4, 8, 12, 16, 20, 24... Les multiples de 5 sont 5, 10, 15, 20, 25... Le nombre 20 apparait donc comme le PPCM de 4 et 5.
- Si vos fractions ont le même dénominateur, cette étape préalable n’est pas nécessaire. Vous pouvez directement soustraire les numérateurs entre eux ^{[3]
  X
  Source de recherche}.
2
Transformez les fractions. Leur valeur ne doit pas être inchangée. Pour obtenir des fractions équivalentes, il faut multiplier ou diviser le numérateur et le dénominateur par une unité. Celle‑ci est écrite sous forme d’une fraction ayant un numérateur et un dénominateur identiques ^{[4]
X
Source de recherche}. Ainsi, si votre dénominateur est multiplié ou divisé, le numérateur doit subir la même opération ^{[5]
X
Source de recherche}.
- Reprenons l’exemple précédent. Si 20 est le PPCM des termes de la soustraction, alors il faut multiplier 1/4 par 5/5. La fraction équivalente obtenue est donc 5/20.
3
Réécrivez la soustraction. Vous devez modifier tous les termes de la soustraction. Ceci, si le PPCM est déjà le dénominateur de l’une des fractions, il n’est pas nécessaire de transformer cette dernière.
- Dans notre exemple, le second terme 1/5 est multiplié par 4/4, ce qui donne 4/20. L’opération initiale devient donc 5/20 – 4/20.
4
Faites la soustraction. Une fois le dénominateur commun trouvé et les fractions modifiées, seuls les numérateurs sont soustraits entre eux.
- Le résultat de l’opération est aussi une fraction dont le dénominateur est le même que celui des termes de la soustraction. Ce dernier ne change donc pas.
- Dans notre exemple, le résultat est donné par l’opération 5 – 4 soit 1/20.
5
Simplifiez le résultat. Cette étape n’est pas toujours possible. Par exemple, la différence de l’opération ci‑dessus est une fraction irréductible. En revanche, vous pouvez obtenir des résultats pouvant être simplifiés. Lorsque le numérateur et le dénominateur ont des multiples communs, divisez‑les par le multiple le plus grand ^{[6]
X
Source de recherche}.
- Dans notre exemple, 1/20 est irréductible. En revanche, une fraction ayant un numérateur et un dénominateur élevés peut être réduite. Par exemple, 24/32 peut être simplifié à 3/4 en divisant la fraction par 8.
Publicité

Méthode 2

Méthode 2 sur 2:
Soustraire des nombres fractionnaires

1
Transformez le nombre fractionnaire. Ce type de nombre est formé d’un entier et d’une fraction ^{[7]
X
Source de recherche}. Il s’agit d’une forme d’écriture plutôt utilisée dans les pays anglosaxons ^{[8]
X
Source de recherche}. Par exemple, 2 1/2 est un nombre fractionnaire qui correspond à l’opération 2 + 1/2 ^{[9]
X
Source de recherche}. Pour réaliser une soustraction comportant un nombre fractionnaire, vous devez au préalable le transformer en une fraction équivalente.
- Supposons que l’opération soit 2 3/4 – 1 1/7. Il faut transformer les termes de l’opération. Par exemple, 2 s’écrit sous la forme suivante 2/1. Pour l’additionner à 3/4, il faut donc le multiplier par 4. 2 3/4 est donc équivalent à 8/4 + 3/4 soit 11/4. De la même façon, 1 1/7 est égal à 7/7 + 1/7 soit 8/7. L’opération s’écrit donc 11/4 – 8/7.
2
Réécrivez l’opération. Une fois tous les termes écrits sous forme de fractions, les étapes de soustraction sont les mêmes que celles indiquées dans la méthode 1. Si nécessaire, vous devez donc réécrire les fractions avec le même dénominateur en cherchant le PPCM.
- Dans notre exemple, les multiples de 4 sont 4, 8, 12, 16, 20, 24, 28... Les multiples de 7 sont 7, 14, 21, 28... 28 est donc le PPCM de 4 et 7.
3
Transformez le premier terme de la soustraction. Multipliez le numérateur et le dénominateur de chaque fraction pour en obtenir une équivalente.
- Dans notre exemple, 11/4 est multiplié par 7 pour donner 77/28.
4
Réécrivez l’opération. Toutes les fractions de votre soustraction doivent avoir le même dénominateur.
- Dans notre exemple, 8/7 est multiplié par 4 pour donner 32/28. Notre opération devient donc 77/28 – 32/28.
5
Faites l’opération. Une fois le dénominateur commun trouvé et la soustraction transformée, vous pouvez passer à l’opération elle‑même. Seuls les numérateurs doivent être soustraits entre eux. Le dénominateur reste inchangé.
- Le résultat de notre opération est donc 45/28.
6
Simplifiez le résultat. Il s’agit de transformer la fraction en un nombre fractionnaire. Commencez par diviser le numérateur par le dénominateur pour en tirer un nombre entier. Le reste du quotient est écrit sous forme d’une fraction qui peut être réduite.
- Notre résultat de 45/28 devient donc 1 17/28. En effet, 45/28 vaut 1,60 soit 28/28 + 17/28.
Publicité

Conseils

Pour trouver le plus petit dénominateur commun, vous pouvez simplement multiplier les dénominateurs entre eux. Cela évite de dresser la liste des multiples de chaque dénominateur ^{[10]
X
Source de recherche}.
Pour réaliser une soustraction contenant un nombre fractionnaire, vous pouvez réaliser d’abord l’opération entre les nombres entiers. Réécrivez l’opération puis transformez les termes afin de soustraire les numérateurs. Vous devez obtenir un résultat sous forme de nombre fractionnaire. Pour reprendre l’opération de l’article, 2 3/4 – 1 1/7 s’écrit (2 + 3/4) – (1 + 1/7). On obtient donc 1 + 3/4 – 1/7. En transformant les fractions, on a 1 + 21/28 – 4/28 soit 1 + 17/28. Sous forme de nombre fractionnaire, ce résultat s’écrit donc 1 17/28.