Nombre premier
Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs. Ces deux diviseurs sont 1 et le nombre considéré, puisque tout nombre a pour diviseurs 1 et lui-même (comme le montre l’égalité n = 1 × n), les nombres premiers étant ceux qui ne possèdent pas d'autre diviseur. Par exemple, le nombre entier 7 est premier car 1 et 7 sont les seuls diviseurs entiers et positifs de 7. Tout nombre pair étant multiple de 2, les nombres premiers sont par conséquent tous impairs, excepté le nombre 2 lui-même. De plus, tout nombre se terminant par 5 étant un multiple de ce dernier, les nombres premiers (hormis 2 et 5) se terminent tous par 1, 3, 7 ou 9.
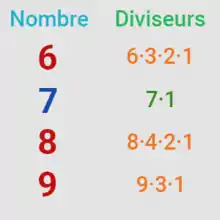
Par opposition, on appelle nombre composé tout nombre entier qui est le produit de deux entiers strictement supérieurs à 1 et possède de ce fait au moins trois diviseurs ; sont composés, par exemple, 4 = 2 × 2 qui en possède 3 (à savoir 1, 2 et 4), 9 = 3 × 3 qui en possède 3 (à savoir 1, 3 et 9) et 12 = 2 × 2 × 3 qui en possède 6 (à savoir 1, 2, 3, 4, 6 et 12).
Selon cette définition, les nombres 0 et 1 ne sont donc ni premiers ni composés : 1 n'est pas premier car il n'a qu'un seul diviseur entier positif et 0 non plus car il est divisible par tous les entiers positifs. Autrefois certains mathématiciens, grâce à une définition légèrement différente des nombres premiers, considéraient que 1 en était un. Mais au début du XXe siècle, un consensus a abouti à la définition donnée ici, qui exclut 1 des nombres premiers[1].
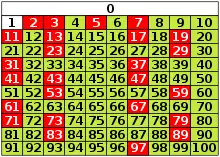
Les vingt-cinq nombres premiers inférieurs à 100 sont : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, et 97.
De telles listes de nombres premiers inférieurs à une borne donnée, ou compris entre deux bornes, peuvent être obtenues grâce à diverses méthodes de calcul. Mais il ne peut pas y avoir de liste exhaustive finie des nombres premiers, car on sait (depuis l'Antiquité : voir Théorème d'Euclide sur les nombres premiers) qu'il en existe une infinité. On ne connaît d’ailleurs pas de formules simples pour produire de telles listes ; la recherche de formules approchées a amené à l’important théorème des nombres premiers.
La notion de nombre premier est une notion de base en arithmétique élémentaire : le théorème fondamental de l'arithmétique assure qu'un nombre composé est factorisable en un produit de nombres premiers, et que cette factorisation est unique à l'ordre des facteurs près. Elle admet des généralisations importantes, mais délicates, dans des branches des mathématiques plus avancées, comme la théorie algébrique des nombres, qui prennent ainsi à leur tour l'appellation d'arithmétique. Par ailleurs, de nombreuses applications industrielles de l'arithmétique reposent sur la connaissance algorithmique des nombres premiers, et parfois plus précisément sur la difficulté des problèmes algorithmiques qui leur sont liés ; c'est le cas de certains systèmes cryptographiques et des méthodes de transmission de l'information. Les nombres premiers sont aussi utilisés pour construire des tables de hachage et pour constituer des générateurs de nombres pseudo-aléatoires.
Découvert le , le plus grand nombre premier connu est le nombre premier de Mersenne 282 589 933 – 1, qui comporte plus de 24 millions de chiffres en écriture décimale.
Éléments historiques
Les entailles retrouvées sur l'os d'Ishango daté à plus de 20 000 ans avant notre ère, mis au jour par l'archéologue Jean de Heinzelin de Braucourt[2] et antérieur à l'apparition de l'écriture (antérieur à 3 200 ans av. J.-C.), semblent isoler quatre groupes de valeurs : 11, 13, 17 et 19. Certains archéologues l'interprètent comme la preuve de la connaissance des nombres premiers. Toutefois, il existe trop peu de découvertes permettant de cerner les connaissances réelles de cette période ancienne[3].
Des tablettes d'argile séchées attribuées aux civilisations qui se sont succédé en Mésopotamie durant le IIe millénaire av. J.-C. montrent la résolution de problèmes arithmétiques et attestent des premières connaissances de l'époque. Les calculs nécessitaient de connaître des tables d'inverses d'entiers (les réciproques) dont certaines ont été retrouvées. Dans le système sexagésimal utilisé par la civilisation babylonienne pour écrire les entiers, les réciproques des diviseurs des puissances de 60 (nombres réguliers) se calculent facilement : par exemple, diviser par 24, c'est multiplier par 2 × 60 + 30 (= 150) puis décaler la virgule de deux rangs vers la droite (soit diviser par 602), puisque 1/24 = 150/602. Leur connaissance nécessitait une bonne compréhension de la multiplication, de la division. Dans les mathématiques égyptiennes, le calcul fractionnaire demandait aussi des connaissances sur les opérations et les divisions d’entiers. Les textes mathématiques égyptiens ne notaient que certaines fractions, en particulier celles correspondant actuellement aux inverses d’entiers (1/2, 1/3, 1/4, 1/5, …) ; l’écriture des fractions se faisait en additionnant ces « inverses d'entiers », si possible sans répétition (1/2 + 1/6 au lieu de 1/3 + 1/3)[4]. Mais il n'y a pas de trace de factorisation d'entiers ou de nombres premiers dans ces textes[5].
La première trace incontestable de la présentation des nombres premiers remonte à l'Antiquité (vers 300 av. J.-C.), et se trouve dans les Éléments d’Euclide (livres VII à IX). Euclide donne une définition des nombres premiers, la preuve de leur infinité, la définition du plus grand commun diviseur (pgcd) et du plus petit commun multiple (ppcm), et les algorithmes pour les déterminer, aujourd’hui appelés algorithmes d’Euclide. Il est possible que les connaissances présentées soient antérieures.
Jalons symboliques
L'esprit ludique et l'émulation ont amené des mathématiciens à définir des seuils de gigantisme pour les nombres premiers[réf. nécessaire], exprimés en nombre de chiffres en base dix. Parmi ces records, battus ou à battre, on notera en particulier :
- les nombres premiers titanesques (titanic primes), au-delà de mille chiffres,
- les nombres premiers gigantesques (gigantic primes), au-delà de dix mille chiffres,
- les méga-nombres premiers (megaprimes), au-delà d'un million de chiffres.
En , plus de mille méga-nombres premiers étaient connus[6]. Le premier à être découvert fut, en 1999, le nombre de Mersenne 26 972 593 − 1 avec ses 2 098 960 chiffres[7],[8], grâce aux efforts du projet collaboratif de calcul distribué Great Internet Mersenne Prime Search (GIMPS).
L'Electronic Frontier Foundation offre des prix de calcul coopératif pour encourager les internautes à contribuer à la résolution de problèmes scientifiques par le calcul distribué. Le GIMPS a ainsi reçu 100 000 dollars pour sa découverte en 2008 du premier nombre premier d'au moins dix millions de chiffres décimaux. L'EFF offre encore 150 000 et 250 000 dollars respectivement pour la découverte du premier nombre premier de cent millions et un milliard de chiffres décimaux[9].
Historique du plus grand nombre premier connu
Le record du plus grand nombre premier connu a presque toujours été trouvé parmi les nombres de Mersenne, comme le dernier en date, M82589933 = 282 589 933 – 1, un nombre découvert le , ayant 24 862 048 chiffres décimaux.
Historique des nombres premiers tous connus ou dénombrés en dessous d'un seuil
Découvrir un nombre premier plus grand que tous ceux déjà connus n'implique pas de connaître tous les nombres premiers intermédiaires.
Plus généralement, la recherche de tous les nombres premiers inférieurs à un nombre donné (premier ou non) constitue un défi mathématique spécifique.
| Date | Seuil s | Quantité π(s)(*) | Vérificateurs | Méthode |
|---|---|---|---|---|
| Antiquité | 1 000 | 168 | Ératosthène, Euclide[10] | Essais par division[10] |
| 1746[10] | 100 000 | 9 592 | ? | |
| 1797[10] | 400 000 | 33 860 | ||
| 1811[10] | 1 000 000 | 78 498 | ||
| 1863[10] | 100 000 000 | 5 761 455 | Jakob Philipp Kulik (de)[10],[11] | |
| 2010[12] | 276 = 75 557 863 725 914 323 419 136 | 1 462 626 667 154 509 638 735 | Jens Franke et al.[12] | Évaluation directe de [12] |
| 277 = 151 115 727 451 828 646 838 272 | 2 886 507 381 056 867 953 916 | |||
| 1024 ≈ 1 000 000 000 000 000 000 000 000 | 18 435 599 767 349 200 867 866 |
Notes :
(*) π(s) est la quantité totale de nombres premiers situés sous le seuil s (c'est-à-dire dans l'intervalle d'entiers ).
La connaissance de π(s) par un calcul algorithmique n'implique pas nécessairement que chacun des nombres premiers soit immédiatement identifiable.
La décomposition en facteurs permet au contraire d'identifier les nombres premiers individuellement, mais elle est impraticable pour des nombres supérieurs à 1040 ; au-delà de cette valeur, on dispose de tests de primalité rapides.
Structures algébriques, topologiques, et nombres premiers
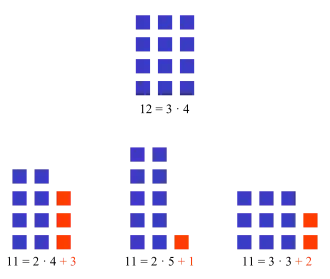
La notion de nombre premier est liée à l'étude de la structure multiplicative de l'anneau des entiers relatifs. Le théorème fondamental de l'arithmétique, basé sur le lemme d'Euclide, élucide cette structure en assurant que tout entier strictement positif se factorise en un produit de nombres premiers, de manière unique à l'ordre des facteurs près. Ce théorème permet de déterminer des notions de pgcd, ppcm, et de nombres premiers entre eux, qui sont utiles pour la résolution de certaines équations diophantiennes, notamment la caractérisation des triplets pythagoriciens.
D'autres problèmes naturels sont envisagés, comme la détermination de la proportion d'entiers premiers à un entier fixé. L'introduction de structures algébriques plus avancées permet de résoudre ce problème rapidement dans le cadre de l'arithmétique modulaire. De nombreux théorèmes classiques de nature arithmétique peuvent être énoncés, comme le petit théorème de Fermat, ou le théorème de Wilson ; ou des théorèmes de nature plus algébrique comme le théorème des restes chinois.
Le théorème des restes chinois est un premier résultat dans l'étude des groupes abéliens finis[13]. Il met en évidence que la structure de ces groupes est en partie liée à la décomposition en produit de facteurs premiers de leurs cardinaux. Les choses sont plus compliquées pour les groupes non abéliens, cependant, l'étude se base à nouveau sur la décomposition en facteurs premiers de leurs cardinaux, à travers la théorie de Sylow.
Les nombres premiers interviennent aussi dans les structures topologiques. Le corps des nombres rationnels admet une structure topologique habituelle, qui donne par complétion le corps des nombres réels. Pour chaque nombre premier p, une autre structure topologique peut être construite, à partir de la norme suivante : si est un nombre rationnel non nul sous forme irréductible et que et sont les plus grandes puissances de p divisant a et b, la norme p-adique de x est . En complétant le corps des rationnels suivant cette norme, on obtient le corps des nombres p-adiques, introduit par Kurt Hensel au début du XXe siècle. Le théorème d'Ostrowski assure que ces normes p-adiques et la norme habituelle sont les seules sur le corps des nombres rationnels, à équivalence près[14].
Nombres premiers particuliers
Il existe des types remarquables de nombres premiers, définis par des contraintes particulières. Les quelques cas ci-dessous sont parmi les plus connus.
Nombres premiers de Pythagore
On appelle parfois nombre premier « de Pythagore » tout nombre premier de la forme 4n + 1, où n est un entier naturel. Par exemple, le nombre premier 5 est de Pythagore. Un nombre premier impair est de Pythagore si et seulement s'il est somme de deux carrés.
Nombres premiers de Mersenne
Les nombres premiers de la forme : où p est alors nécessairement aussi premier, sont appelés nombres premiers de Mersenne. Les grands nombres premiers sont souvent recherchés sous cette forme car il existe un test efficace, le test de primalité de Lucas-Lehmer, pour déterminer si un tel nombre est premier ou non.
Entre 2008 et 2012, le plus grand nombre premier connu était M43 112 609 = 243 112 609 – 1, qui comporte 12 978 189 chiffres en écriture décimale. Il s'agit (chronologiquement) du 45e nombre premier de Mersenne connu et sa découverte a été annoncée le par le GIMPS. Un 46e nombre premier de Mersenne, 237 156 667 – 1, inférieur au précédent, a été découvert deux semaines plus tard ; le était découvert, par le même projet GIMPS, un 47e nombre premier de Mersenne, 242 643 801 – 1, lui aussi inférieur au premier cité.
Ce record a été battu (toujours par le GIMPS) par la preuve de la primalité de M57 885 161 = 257 885 161 – 1 (en janvier 2013) puis à nouveau, le , par celle de M74 207 281, le , par celle de M77 232 917, et enfin, le , par celle de M82 589 933.
Nombres premiers de Fermat
Les nombres de la forme : sont appelés les nombres de Fermat. Fermat avait conjecturé que tous ces nombres étaient premiers[15]. Cependant, les seuls nombres de Fermat premiers connus sont
- , , , et .
Le nombre de Fermat F5 est seulement semi-premier. Il est divisible par 641.
Il s'agit du premier contre-exemple à cette conjecture de Fermat, découvert par Euler[16] en 1732. Tous les autres nombres de Fermat calculés depuis sont composés, au point que l'objectif s'est transformé en la recherche effrénée d'un autre nombre de Fermat premier.
Nombres premiers jumeaux
Deux nombres premiers sont dits jumeaux s'ils ne diffèrent que de 2. Les trois plus petits couples de nombres premiers jumeaux sont (3, 5), (5, 7) et (11, 13). Le plus grand connu est 2 996 863 034 895 × 221 290 000 ± 1 ; les deux nombres possèdent 388 342 chiffres (septembre 2016).
Il est conjecturé qu'il existe une infinité de nombres premiers jumeaux.
Nombres premiers de Sophie Germain
Un nombre premier G est un nombre premier de Sophie Germain si 2G + 1 est aussi un nombre premier, appelé nombre premier sûr.
Les dix premiers nombres premiers de Sophie Germain sont 2, 3, 5, 11, 23, 29, 41, 53, 83, 89.
Il est conjecturé qu'il existe une infinité de nombres premiers de Sophie Germain.
Nombres premiers brésiliens
Un nombre premier brésilien p est un nombre premier qui est répunit avec un nombre premier impair de 1 dans une base b ; la réciproque est fausse comme le montrent 57 = 1117 = 3 × 19 ou encore 121 = 111113 = 11 x 11.
Le plus petit nombre premier brésilien est 7 = 1112 ; 43 = 1116 et 127 = 11111112 sont d'autres exemples.
La suite des nombres premiers brésiliens commence par 7, 13, 31, 43, 73, 127, 157, 211, 241, 307, 421, 463 , etc. (suite A085104 de l'OEIS).
Seuls deux nombres premiers brésiliens sont connus pour être brésiliens dans deux bases différentes, ce sont les deux nombres de la conjecture de Goormaghtigh: 31 = 111112 = 1115 et 8191 = 11111111111112 = 11190.
On conjecture qu'il existe une infinité de nombres premiers brésiliens, mais, alors que la série des inverses des nombres premiers est divergente, la série des inverses des nombres premiers brésiliens est convergente vers un nombre, appelé « constante des nombres premiers brésiliens », légèrement supérieure à 0,33 et qui est étudiée dans la séquence ![]() A306759.
A306759.
Tout nombre premier de Mersenne supérieur ou égal à 7 est brésilien par définition. Par exemple, .
Par contre, tout nombre de Fermat premier est non brésilien[17].
Les plus petits nombres des couples de nombres premiers jumeaux qui sont brésiliens sont plutôt rares (ils figurent dans la suite ![]() A306849), et plus généralement, les nombres premiers brésiliens sont relativement rares ; ainsi, sur les premiers 1012 entiers naturels, il existe 37 607 912 018 nombres premiers dont seulement 88 285 sont des premiers brésiliens.
A306849), et plus généralement, les nombres premiers brésiliens sont relativement rares ; ainsi, sur les premiers 1012 entiers naturels, il existe 37 607 912 018 nombres premiers dont seulement 88 285 sont des premiers brésiliens.
Algorithmique : calcul des nombres premiers et tests de primalité
Crible d'Ératosthène et algorithme par essais de division
Les premiers algorithmes pour décider si un nombre est premier (appelés tests de primalité) consistent à essayer de le diviser par tous les nombres qui n'excèdent pas sa racine carrée : s'il est divisible par l'un d'entre eux, il est composé, et sinon, il est premier. Cependant, l'algorithme déduit de cette formulation peut être rendu plus efficace : il suggère beaucoup de divisions inutiles, par exemple, si un nombre n'est pas divisible par 2, il est inutile de tester s'il est divisible par 4. En fait, il suffit de tester sa divisibilité par tous les nombres premiers n'excédant pas sa racine carrée.
Le crible d'Ératosthène est une méthode, reposant sur cette idée, qui fournit la liste des nombres premiers inférieurs à une valeur fixée n (n = 120 dans l'animation ci-contre) :
- on forme la liste des entiers de 2 à n ;
- on retient comme « nombre premier » le premier nombre de la liste non encore barré (le premier dans ce cas est 2) ;
- on barre tous les entiers multiples du nombre retenu à l'étape précédente, en commençant par son carré (puisque 2 × i, 3 × i, … , (i – 1) × i ont déjà été barrés en tant que multiples de 2, 3, ...) ;
- on répète les deux dernières opérations (c'est-à-dire : on retient le prochain nombre non barré et on barre ses multiples) ;
- dès qu'on en est à chercher les multiples des nombres excédant la racine carrée de n, on termine l'algorithme.
Ainsi les nombres premiers inférieurs à n sont les nombres qui restent non barrés à la fin du processus. Cet algorithme est de complexité algorithmique exponentielle.
Le crible d'Ératosthène fournit donc plus d'information que la seule primalité de n. Si seule cette information est souhaitée, une variante parfois plus efficace consiste à ne tester la divisibilité de n que par des petits nombres premiers dans une liste fixée au préalable (par exemple 2, 3 et 5), puis par tous les nombres entiers inférieurs à la racine carrée de n qui ne sont divisibles par aucun des petits nombres premiers choisis ; cela amène à tester la divisibilité par des nombres non premiers (par exemple 49 si les petits premiers sont 2, 3 et 5 et que n excède 2500), mais un choix d'un nombre suffisant de petits nombres premiers doit permettre de contrôler le nombre de tests inutiles effectués[18].

Autres algorithmes
Une variante du crible d'Ératosthène est le crible de Sundaram qui consiste à former les produits de nombres impairs. Les nombres qui ne sont pas atteints par cette méthode sont les nombres premiers impairs, c'est-à-dire tous les nombres premiers sauf 2. Par ailleurs, à partir du crible d'Ératosthène, la factorisation de l'entier n peut facilement être trouvée. D'autres méthodes plus générales concernant ce problème plus difficile que simplement déterminer la primalité sont aussi appelées méthodes de crible, la plus efficace étant actuellement le crible général des corps de nombres[19].
Les algorithmes présentés précédemment ont une complexité trop importante pour pouvoir être menés à terme, même avec les ordinateurs les plus puissants, quand n devient grand.
Une autre classe d'algorithme consiste à tester l'entier n pour une famille de propriétés vérifiées par les nombres premiers : si une propriété de cette famille n'est pas vérifiée pour n, alors il est composé ; en revanche, le fait qu'une des propriétés de la famille soit vérifiée pour n ne suffit pas à assurer la primalité. Toutefois, si cette famille est telle qu'un nombre composé ne vérifie pas au moins la moitié des propriétés en jeu, alors l'utilisateur peut estimer qu'un nombre n qui vérifie k propriétés de la famille est premier avec une probabilité supérieure à 1 – 2–k : il est déclaré probablement premier à partir d'une valeur de k à choisir par l'utilisateur ; un nombre déclaré probablement premier, mais qui n'est pas premier est appelé nombre pseudo-premier. Un test basé sur ce principe est appelé test probabiliste de primalité. De tels tests reposent souvent sur le petit théorème de Fermat, amenant au test de primalité de Fermat, et à ses raffinements : le test de primalité de Solovay-Strassen et celui de Miller-Rabin, qui sont des améliorations, car ils admettent moins de nombres pseudo-premiers[20],[21].
L'algorithme AKS mis au point en 2002 permet de déterminer (avec certitude) si un nombre donné N est premier en utilisant un temps de calcul polynomial.
Des formules sur les nombres premiers
De nombreuses formules ont été cherchées pour générer les nombres premiers. Le plus haut niveau d'exigence serait de trouver une formule qui à un entier n associe le n-ième nombre premier. De manière un peu plus souple, on peut se contenter d'exiger une fonction f qui à tout entier n associe un nombre premier et telle que chaque valeur prise ne le soit qu'une fois.
Enfin, on souhaite que la fonction soit calculable en pratique[22] (ce qui n'est pas le cas de la formule de Mills). Par exemple, le théorème de Wilson assure que p est un nombre premier si et seulement si (p -1)! ≡ -1 mod p. Il s'ensuit que la fonction f(n) = 2 + [((n - 1)!) mod n] vaut n si n est un nombre premier et vaut 2 sinon. Cependant, le calcul de la factorielle (même modulo ) est rédhibitoire pour de grandes valeurs de n, et cette fonction a donc peu d'utilité pour générer des nombres premiers.
Il est donc tentant de chercher des fonctions polynomiales dont les valeurs sont des nombres premiers. Ceci a conduit au résultat (négatif) suivant : un polynôme (à une ou plusieurs variables) dont les valeurs aux entiers naturels sont des nombres premiers, est un polynôme constant[23].
La recherche de polynômes vérifiant une propriété plus faible s'est développée à partir de la notion d'ensemble diophantien de nombres entiers ; de tels ensembles peuvent être caractérisés comme les ensembles de valeurs strictement positives prises par un polynôme (à plusieurs variables) dont les coefficients et les variables sont des nombres entiers.
Un travail mené dans les années 1960 et 1970, notamment par Putnam, Davis, Robinson et Matiiassevich permet de montrer que l'ensemble des nombres premiers est diophantien, conduisant à l'existence de polynômes à coefficients et variables entières dont toutes les valeurs positives sont les nombres premiers. L'écriture de divers polynômes explicites a ensuite été possible, avec différents nombres de variables, et divers degrés. Notamment, Jones, Sato, Wada et Wiens ont déterminé en 1976 un tel polynôme, de degré 25 à 26 variables. De même que pour les formules à factorielles, ce polynôme est inutilisable en fait, car il ne donne pratiquement que des valeurs négatives quand on fait varier les 26 variables de 0 à
La notion d'ensemble diophantien s'est plus généralement développée à partir de l’étude et de la résolution du dixième problème de Hilbert sur les équations diophantiennes[24], Matiiassevitch ayant montré que tous les ensembles récursivement énumérables sont diophantiens.
Répartition des nombres premiers
Infinité des nombres premiers
Euclide a démontré dans ses Éléments (proposition 20 du Livre IX) que les nombres premiers sont en plus grande quantité que toute quantité proposée de nombres premiers. Autrement dit, il existe une infinité de nombres premiers. La démonstration d'Euclide repose sur la constatation qu'une famille finie p1,...,pn de nombres premiers étant donnée, tout nombre premier divisant le produit des éléments de cette famille augmenté de 1 est en dehors de cette famille (et un tel diviseur existe, ce qui est aussi prouvé par Euclide)[25].
D'autres démonstrations de l'infinité des nombres premiers ont été données. La preuve d'Euler[26] utilise l'identité :
Dans la formule précédente, le terme de gauche est la somme de la série harmonique, qui est divergente. Par conséquent, le produit de droite doit contenir une infinité de facteurs.
Furstenberg fournit une preuve utilisant une argumentation topologique[27].
Raréfaction des nombres premiers

XVIIIe siècle
Le premier résultat sur le comportement des nombres premiers à l’infini est dû à Euler :
Théorème de raréfaction d’Euler (1737) — La série des inverses des nombres premiers est divergente : |
Comme la série des inverses de tous les entiers est également divergente, cela indique intuitivement que, si les nombres premiers se raréfient à l’infini, ils ne se raréfient pas très vite[28].
Par ailleurs, le résultat sur l'infinité des nombres premiers amène à se demander combien il y a de nombres premiers jusqu’à un nombre donné et à étudier la fonction correspondante. Pour cela, on désigne, pour tout nombre premier son rang dans la suite croissante des nombres premiers, comme indiqué dans le tableau suivant pour les 25 nombres premiers inférieurs à 100 :
| Les 25 nombres premiers inférieurs à 100 | : | 2, | 3, | 5, | 7, | 11, | 13, | 17, | 19, | 23, | 29, | 31, | 37, | 41, | 43, | 47, | 53, | 59, | 61, | 67, | 71, | 73, | 79, | 83, | 89, | 97. | |
| Rang | : | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
Pour une variable réelle, est définie comme le nombre de nombres premiers Cette fonction réelle à valeurs entières est appelée fonction de compte des nombres premiers. C’est une fonction en escalier, constante entre deux nombres premiers successifs : est égal à , étant le plus grand nombre premier
Restreinte au domaine de définition , la fonction a une fonction réciproque, généralement notée , qui représente le n-ième nombre premier, par exemple .
La fonction est croissante et tend vers l’infini[25]. C’est une conséquence triviale du théorème de l’infinité des nombres premiers (voir section précédente).
Le premier résultat important sur est obtenu par Legendre :
Théorème de raréfaction de Legendre — Le rapport tend vers zéro quand tend vers l’infini. |
Vers la fin du XVIIIe siècle, Legendre (1797) et Gauss (1792) conjecturent que la fonction de compte des nombres premiers est équivalente à la fonction quand tend vers l'infini. Dit autrement, la proportion de nombres premiers parmi les nombres inférieurs à c’est-à-dire tend vers 0 à la vitesse de .
On peut apprécier la pertinence de cette conjecture en examinant le tableau des valeurs de et de pour les valeurs de égales aux premières puissances entières de 10 :
| 10 | 4 | 0,400 | 0,921 |
| 100 | 25 | 0,250 | 1,151 |
| 1 000 | 168 | 0,168 | 1,161 |
| 10 000 | 1 229 | 0,123 | 1,132 |
| 100 000 | 9 592 | 0,096 | 1,104 |
| … | … | … | … |
(Euclide) | 0 (Legendre) | 1 (conjecture) |
Il faudra tout le XIXe siècle pour que la conjecture soit démontrée (voir section suivante).
XIXe siècle
Une première avancée vers la démonstration de la conjecture de Legendre-Gauss [29] est obtenue par Tchebychev à partir de 1848 :
Théorème de Tchebychev — Il existe deux constantes C et D telles qu'on ait l'encadrement, pour x assez grand :
la conjecture de Legendre-Gauss consistant à affirmer la validité de l’énoncé pour n’importe quel et n’importe quel
Il démontre également le théorème suivant sur la raréfaction des nombres premiers :
Comme conséquence des inégalités ci-dessus, Tchebychev peut aussi démontrer le postulat de Bertrand selon lequel dans tout intervalle d'entiers naturels, entre un entier et son double existe au moins un nombre premier[30].
Une nouvelle avancée est due à Riemann dans un article célèbre en 1859 : il étend le domaine de définition de la fonction au plan complexe privé du nombre ; il formule sa célèbre hypothèse, selon laquelle les zéros de situés dans la bande ont pour partie réelle son approche constitue une impulsion décisive au développement de la théorie analytique des nombres, source de nombreuses avancées en théorie des nombres.
À la fin du siècle, la conjecture de Legendre et Gauss est démontrée indépendamment par Jacques Hadamard et Charles-Jean de La Vallée Poussin[31], et porte depuis lors le nom de théorème des nombres premiers. La démonstration s’appuie sur l’observation qu’il suffit de s’assurer que la fonction ne s'annule pas dans le demi-plan de partie réelle et de trouver un domaine qui englobe ce demi-plan dans lequel c’est le cas.
Théorème des nombres premiers (Hadamard et de La Vallée Poussin, 1896) — Quand
Les démonstrations utilisent des outils puissants d'analyse complexe pour démontrer un énoncé d'arithmétique et d'analyse réelle. Une stratégie pour ces démonstrations est l'étude de la fonction zêta de Riemann sur un domaine du plan complexe plus grand qu'un simple voisinage de z=1 : il est nécessaire de la contrôler, c'est-à-dire de majorer son module, au voisinage de la droite verticale des nombres de partie réelle égale à 1[32]. La puissance des outils d'analyse complexe utilisés pour résoudre le théorème des nombres premiers conduit à un développement important d'une branche entière des mathématiques, la théorie analytique des nombres, dans laquelle l'étude de la fonction zêta de Riemann devient un thème central. En particulier l'hypothèse de Riemann, encore non démontrée, sur la localisation de ses zéros, aurait des conséquences fortes sur le comportement de la fonction de compte des nombres premiers.
XXe siècle
Sur la base des résultats de Riemann (article de 1859), on peut déduire l'estimation :
Théorème (Helge von Koch, 1901) — Sous l’hypothèse de Riemann, on a :
où (Riemann note cette fonction ) et où signifie qu’il existe une constante telle que pour tout assez grand.
Les résultats sur la fonction de compte des nombres premiers permettent d'obtenir des résultats sur le n-ième nombre premier. Par exemple, comme conséquences directes des théorèmes de Tchebychev, Ishikawa établit en 1934 des propriétés de la fonction n-ième nombre premier, désignée par :
Ou encore, d'après un résultat de Felgner de 1990[33] :
Des démonstrations élémentaires du théorème des nombres premiers sont trouvées. Par élémentaires, il faut entendre qu’elles ne recourent pas à l'analyse complexe. C’est le cas notamment d’Erdős et de Selberg[31].
Répartition des nombres premiers dans les progressions arithmétiques
En 1838, en reprenant l’étude d’Euler, au moyen d'un outil appelé caractère de Dirichlet, et en utilisant à la place de la fonction zêta de Riemann des fonctions analogues appelées fonction L de Dirichlet, Dirichlet est capable d'adapter la démonstration au cas des nombres premiers dans des progressions arithmétiques : si a et b sont premiers entre eux, alors il existe une infinité de nombres premiers de la forme aq+b. Utilisant les techniques de Hadamard, La Vallée Poussin démontre ensuite une version quantitative du théorème; les nombres premiers sont équirépartis entre les différentes progressions arithmétiques de raison a (c'est-à-dire avec a fixé, et b variant parmi les divers restes inversibles dans la division euclidienne par a)[34],[35] : le nombre de nombres premiers inférieurs ou égaux à x, dans la suite aq +b, est donc équivalent à x/(ln(x)φ(a)), où φ est l'indicatrice d'Euler. Bien que cela montre qu'il y a, par exemple, « autant » de nombres premiers de la forme 3n +1 que de la forme 3n+2, les seconds semblent expérimentalement moins nombreux ; c'est le biais de Tchevychev, dont une démonstration rigoureuse dans tous les cas n'est pas encore connu en 2020.
Théorème de Green-Tao
Le théorème de Green-Tao, démontré en 2004 par Ben Joseph Green et Terence Tao, généralise notamment le théorème de Dirichlet en assurant que pour tout entier k, il existe une infinité de suites de k nombres premiers en progression arithmétique, c'est-à-dire de la forme :
Le théorème de Green-Tao est en fait bien plus fort que cet énoncé seul : par exemple, il établit qu'une telle progression arithmétique existe, avec des entiers tous plus petits que :
(expérimentalement, cette borne semble plutôt devoir être de l'ordre de k!). Il assure également que pour tout entier k et tout réel strictement positif, pour tout x suffisamment grand, si P est un ensemble de nombres premiers inférieurs à x contenant au moins éléments, alors P contient au moins une progression arithmétique de nombres premiers comptant k termes.
Conjecture de Bateman-Horn
De nombreux résultats et conjectures sur la répartition des nombres premiers sont contenus dans la conjecture générale suivante. Soit f1,...,fk des polynômes non constants, irréductibles et vérifiant la propriété que pour tout nombre premier p il y ait au moins un entier n parmi 0, ..., p – 1 tel que p ne divise pas le produit des fi(n). On note le complémentaire à p du nombre de tels entiers. Un tel ensemble de polynômes est dit admissible ; on cherche à connaître la proportion d'entiers en lesquels les polynômes prennent simultanément des valeurs premières, et se limiter à des ensembles de polynômes admissibles permet d'éviter des cas triviaux comme f1(t)=t, et f2(t)=t+1. Il est alors conjecturé que le nombre d'entiers n plus petits qu'un réel x tels que les valeurs f1(n),...,fk(n) sont simultanément premières, est, pour x assez grand, de l'ordre de :
Le théorème des nombres premiers correspond au cas k = 1 et ft = t, le théorème de Dirichlet à k = 1 et ft = at + b, et pour k = 2, f1(t) = t et f2(t) = t + 2, on obtient une version quantitative (et donc plus générale) de la conjecture des nombres premiers jumeaux.
Applications
La décomposition en facteurs premiers est utile pour simplifier les calculs fractionnaires, et de manière générale simplifier des formules. Elle n'est raisonnablement applicable que pour de petits nombres. Les sciences physiques ont de nombreuses formules comportant des nombres entiers petits, soit qu'il s'agisse de coefficients provenant de la dérivation ou de l'intégration de monômes, soit qu'il s'agisse de coefficients choisis volontairement entiers pour une application.
Les nombres premiers, et plus généralement la théorie des nombres, ont longtemps été vus comme un sujet purement mathématique, avec peu ou pas d'applications extérieures. Cela changea rapidement dans les années 1970, quand de nouveaux systèmes de cryptographie basés sur les propriétés des nombres premiers furent conçus.
Cryptographie à clé publique
Jusque dans les années 1970, les systèmes de chiffrement connus étaient basés sur le principe de la cryptographie symétrique, où une même clé (secrète) est utilisée pour chiffrer et déchiffrer un message. En 1978, Ronald Rivest, Adi Shamir et Leonard Adleman décrivent le premier système public de cryptographie asymétrique (nommé d'après leurs initiales RSA), basé sur les propriétés des nombres premiers et de la factorisation. Dans un tel système, deux clés sont utilisées : l'une sert à chiffrer, l'autre à déchiffrer. La clé permettant de chiffrer est accompagnée d'un grand nombre entier, le produit de deux grands nombres premiers gardés secrets (de l'ordre de 200 chiffres). Pour calculer la clé de déchiffrement, la seule méthode connue nécessite de connaître les deux facteurs premiers. La sécurité du système est basée sur le fait qu'il est facile de trouver deux grands nombres premiers (en utilisant des tests de primalité) et de les multiplier entre eux, mais qu'il serait difficile pour un attaquant de retrouver ces deux nombres. Ce système permet également de créer des signatures numériques, et a révolutionné le monde de la cryptographie.
Généralisations des nombres premiers
La notion de nombre premier s'est vue généralisée au cours du XIXe siècle dans d'autres structures algébriques que l'anneau des entiers relatifs. Pour résoudre des problèmes arithmétiques tels que le théorème des deux carrés, le théorème des quatre carrés, ou encore la loi de réciprocité quadratique (dont la première preuve est due à Carl Friedrich Gauss dans ses Disquisitiones arithmeticae), les mathématiciens ont été amenés à mener des raisonnements sur la divisibilité analogues à ceux qui impliquent les nombres entiers dans d'autres anneaux, par exemple celui des entiers de Gauss ou celui des entiers d'Eisenstein.
Le point de vue moderne trouve sa source dans les travaux d'Ernst Kummer, qui introduit la notion de « nombre premier idéal », dans sa tentative de démontrer le grand théorème de Fermat. Cette notion est à l'origine de la théorie moderne des anneaux d'entiers algébriques, découlant des travaux de Dedekind et Kronecker[36] : en termes modernes, on dit que ces anneaux ont une structure d'anneaux de Dedekind ; notamment, le théorème sur la factorisation des nombres premiers y est remplacé par un résultat de factorisation des idéaux de l'anneau (c'est-à-dire les sous-groupes absorbants pour la multiplication, qui dans ce contexte sont en rapport avec ce que Kummer appelait « nombres idéaux ») en produit d'idéaux premiers. L'arithmétique dans ces anneaux a en général des liens profonds et difficiles avec l'arithmétique des nombres premiers classiques : par exemple, dans ses travaux sur le théorème de Fermat, Kummer parvient à démontrer l'impossibilité de trouver des solutions non triviales (c'est-à-dire avec x, y et z non nuls) à l'équation xp + yp = zp si p est un nombre premier régulier (il s'agit d'une condition portant sur la nature de l'anneau des entiers algébriques engendré par une racine primitive p-ième de l'unité).
Sur la seule base de quelques expériences statistiques, certaines conjectures sur les nombres premiers ont été transposées aux nombres chanceux (construits par une variante du crible d'Ératosthène)[37].
Conjectures et questions ouvertes
Il y a beaucoup de conjectures et de questions ouvertes sur les nombres premiers. Par exemple :
- Les quatre problèmes de Landau :
- conjecture de Goldbach : tout nombre pair strictement supérieur à 2 peut s'écrire comme somme de deux nombres premiers ;
- conjecture des nombres premiers jumeaux : il existe une infinité de jumeaux premiers ;
- conjecture de Legendre : il existe toujours au moins un nombre premier entre n2 et (n + 1)2 ; cette conjecture est liée à l'hypothèse de Riemann et, comme cette dernière, reste non démontrée à ce jour ;
- existence d'une infinité de nombres premiers de la forme n2 + 1.
- L'existence d'une infinité de nombres premiers de Sophie Germain.
- La conjecture de Polignac (dont celle des nombres premiers jumeaux est le cas particulier n = 2) : tout entier naturel pair n peut s'écrire comme différence de deux nombres premiers consécutifs et cela d'une infinité de manières.
- L'hypothèse H de Schinzel : elle englobe la conjecture des nombres premiers jumeaux et le quatrième problème de Landau ; elle stipule que si l'on a une famille finie de polynômes à coefficients entiers, alors il existe une infinité d'entiers n tels que tous les polynômes de la famille donnent des nombres premiers quand on les évalue en n (à condition qu'il n'y ait pas d'obstruction évidente pour que ce soit le cas : par exemple, si un des polynômes est n(n + 1) ou 2n, ce n'est clairement pas possible).
- La conjecture de Bateman-Horn : elle précise l'hypothèse de Schinzel en donnant une valeur approchée du nombre des n < x ayant cette propriété.
- Y a-t-il une infinité de nombres premiers de Fermat ou de Mersenne ou de Fibonacci ?
- Y a-t-il une infinité de nombres premiers factoriels ou primoriels ?
- Une conjecture de Daniel Shanks : soit la suite, dite d'Euclide-Mullin, de premier terme u1 = 2 et telle que le terme un soit le plus petit diviseur premier du successeur du produit des termes ui pour i < n. La conjecture énonce que tous les nombres premiers apparaissent dans cette suite.
- La spirale d'Ulam (ou horloge d'Ulam) n'est à ce jour pas encore pleinement expliquée.
Notes et références
- (en) Chris Caldwell et Yeng Xiong, « What is the smallest prime ?] », Journal of Integer Sequences, vol. 15, no 9, (lire en ligne).
- Voir Marcus du Sautoy, La Symphonie des nombres premiers, p. 42.
- Olivier Keller, « Préhistoire de la géométrie : le problème des sources ».
- Paul Benoit (dir.), Karine Chemla (dir.) et Jim Ritter (dir.), Histoire des fractions, fractions d'histoire, Bâle, Birkhäuser, .
- Kawai Lui remarque aussi dans sa thèse (en) qu'en dépit de compétences techniques bien supérieures, il ne semble pas que les nombres premiers (ni d'ailleurs les coniques) aient été remarqués en Chine avant le XVIIe siècle, lorsque les missionnaires occidentaux les firent connaître.
- (en) Chris Caldwell, The Largest Known Primes at The Prime Pages.
- (en) GIMPS press release, GIMPS Finds First Million-Digit Prime.
- (en) Chris Caldwell, The Largest Known Prime by Year: A Brief History at The Prime Pages. Part 1 : Before Electronic Computers, Part 2 : The Age of Electronic Computers.
- (en) EFF Cooperative Computing Awards.
- villemin.gerard.free.fr Nombres premiers : Historique.
- Mathématicien autrichien (1793-1863) : (en) John J. O'Connor et Edmund F. Robertson, « Jakob Philipp Kulik », dans MacTutor History of Mathematics archive, université de St Andrews (lire en ligne).
- (en) primes.utm.edu Conditional Calculation of pi(10^24).
- Naudin et Quitté 1992, début du chapitre 3.
- Gouvêa 1997.
- Il écrit ainsi à Bernard Frénicle de Bessy : « Mais voici ce que j'admire le plus : c'est que je suis quasi persuadé que tous les nombres progressifs augmentés de l'unité, desquels les exposants sont des nombres de la progression double, sont nombres premiers, comme 3, 5, 17, 257, 65537, 4 294 967 297 et le suivant de 20 lettres 18 446 744 073 709 551 617 ; etc. Je n'en ai pas la démonstration exacte, mais j'ai exclu si grande quantité de diviseurs par démonstrations infaillibles, et j'ai de si grandes lumières, qui établissent ma pensée, que j'aurois peine à me dédire. », Lettre XLIII, du ? août 1640, dans Œuvres de Fermat, t. 2, Paris, Gauthier-Villars, (lire en ligne), p. 206.
- (la) L. Euler, « Observationes de theoremate quodam Fermatiano aliisque ad numeros primos spectantibus », Commentarii academiae scientiarum Petropolitanae, vol. 6, , p. 102-103 (lire en ligne).
- B. Schott, « Les nombres brésiliens », Quadrature, vol. 76, , disponible dans les liens de la suite A125134 de l'OEIS.
- Cohen 1993, début du chapitre 8, notamment l'algorithme 8.1.1.
- Cohen 1993, chapitre 10, plus particulièrement la section 5.
- Naudin et Quitté 1992, chap. 4, section 6.
- Cohen 1993, chap. 8, section 2.
- Ribenboim 1996, introduction du chapitre 3.
- Ribenboim 1996, chap. 3, section II.
- Ribenboim 1996, chap. 3, section III.
- Hardy et Wright 2007, section 2.1.
- (la) Leonh. Euler, « Variae observationes circa series infinitas », Commentarii academiae scientiarum Petropolitanae, vol. 9, 1744, p. 160-188 ou Opera Omnia, Series 1, vol. 14, p. 217-244. Téléchargeable à . L'identité y est le théorème 7, p. 172 et l'infinité des nombres premiers y est implicitement rappelée et analysée dans les corollaires qui suivent.
- Ribenboim 1996.
- Quand tend vers l’infini, les inégalités suivantes illustrent le rythme de raréfaction :
La série de gauche est convergente, alors que la somme porte sur tous les entiers et que (positif) peut être choisi aussi petit qu’on veut, tandis que la série du milieu, conformément au théorème d’Euler, est divergente et tend vers l’infini, alors que la somme ne porte que sur les nombres premiers. - Ribenboim 1996, chap. 4, section I.
- Hardy et Wright 2007, chap. 22, sections 1 à 4.
- Ellison et Mendès France 1975, chap. 2, section 1.2.
- Ellison et Mendès France 1975, chap. 2, théorème 2.4, puis section 4.
- Ribenboim 1996, chap. 4, section II, A.
- Hardy et Wright 2007, théorème 15.
- Ellison et Mendès France 1975, chap. 7.
- Nicolas Bourbaki, Éléments d'histoire des mathématiques, chapitre Algèbre commutative. Théorie des nombres algébriques.
- (en) David Wells, Prime Numbers : The Most Mysterious Figures in Math, John Wiley & Sons, , p. 147–148.
Ouvrages cités
- [Cohen 1993] (en) Henri Cohen, A Course in Computational Algebraic Number Theory, [détail des éditions] — Référence moderne sur les méthodes effectives en théorie des nombres.
- [Ellison et Mendès France 1975] William John Ellison et Michel Mendès France, Les Nombres premiers, [détail de l’édition] — Livre très clair, comme introduction à la théorie analytique des nombres.
- [Gouvêa 1997] (en) Fernando Q. Gouvêa, P-adic Numbers : An Introduction, [détail de l’édition] — Introduction aux nombres p-adiques à la portée d'un large public, tournée vers des objectifs analytiques.
- [Hardy et Wright 2007] G. H. Hardy et E. M. Wright (trad. de l'anglais par François Sauvageot, préf. Catherine Goldstein), Introduction à la théorie des nombres [« An Introduction to the Theory of Numbers »] [détail de l’édition] — Un grand classique d'introduction à la théorie des nombres, qui couvre les sujets de base (congruences), introduit les méthodes algébriques par l'exemple (entiers de Gauss, de Kronecker), et donne une démonstration du théorème des nombres premiers.
- [Naudin et Quitté 1992] Patrice Naudin et Claude Quitté, Algorithmique algébrique, [détail de l’édition]
- [Ribenboim 1996] (en) Paulo Ribenboim, The New Book of Prime Number Records, Springer, , 3e éd. (lire en ligne)
Voir aussi
Articles connexes
Bibliographie
- Pierre Colmez, Éléments d'analyse et d'algèbre (et de théorie des nombres), Éditions de l'École Polytechnique,
- Jean-Paul Delahaye, Merveilleux nombres premiers : Voyage au cœur de l'arithmétique, [détail de l’édition]
- Michel Demazure, Cours d'algèbre. Primalité, divisibilité, codes, Cassini, . — Ce livre contient de nombreux algorithmes écrits en Caml Light.
- Michel Demazure, Cours d'algèbre. Primalité, divisibilité, codes, Cassini, . — Version étendue (en particulier sur les codes correcteurs) de la première édition, la plupart des algorithmes ont été réécrits en Ruby.
- Plusieurs ouvrages avec le même titre, mais des contenus très différents, ont paru dans la collection Que sais-je ? :
- Émile Borel, Les Nombres Premiers, PUF, coll. « Que sais-je ? » (no 571), ;
- Jean Itard, Les Nombres Premiers, PUF, coll. « Que sais-je ? » (no 571), .
- Gérald Tenenbaum et Michel Mendès France, Les Nombres Premiers, PUF, coll. « Que sais-je ? » (no 571), (1re éd. 1997), 127 p. (ISBN 2-13-048399-2).
- Gérald Tenenbaum et Michel Mendès France, Les Nombres premiers, entre l'ordre et le chaos, Paris, Dunod, , 2e éd., 170 p. (ISBN 978-2-10-070656-3) — Version étendue et mise à jour du précédent, avec par exemple des références au théorème de Green-Tao, ou aux résultats de Zhang Yitang.
Liens externes
- Pierre Colmez, Les nombres premiers
- (en) Page d'Andrew Granville
- (en) The prime numbers : suite A000040 de l'OEIS
- Une grande liste des nombres premiers (jusqu'à 1 000 000 000)
- « Les nombres premiers », sur www.math93.com
- Test de primalité
- Arithmétique et théorie des nombres
- Portail de la cryptologie

