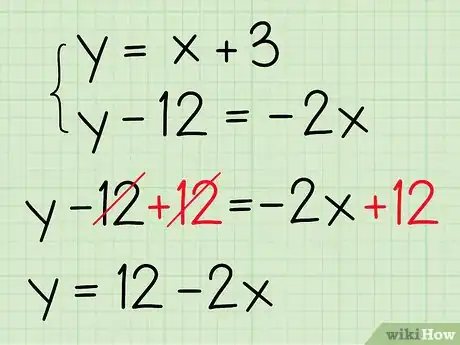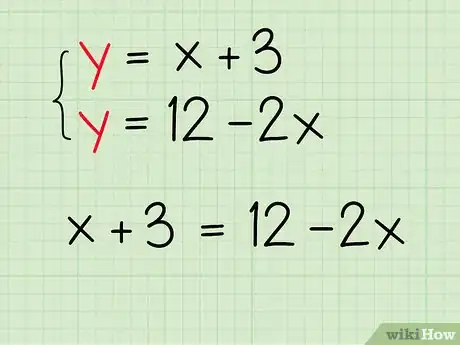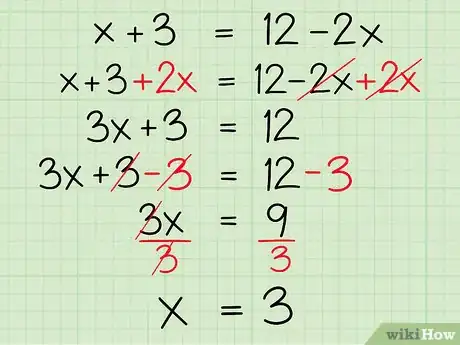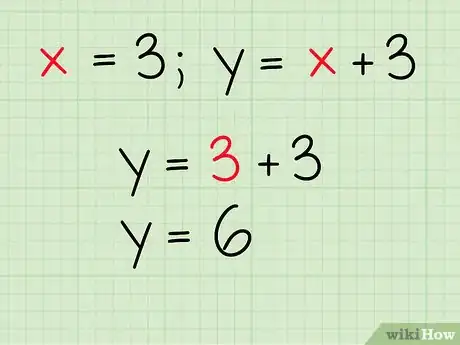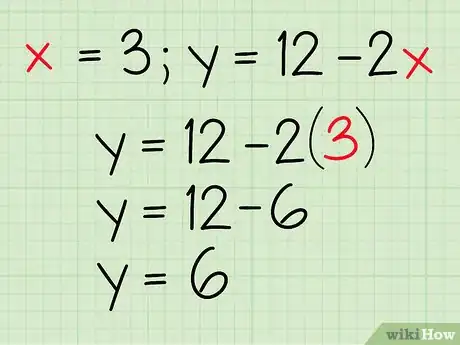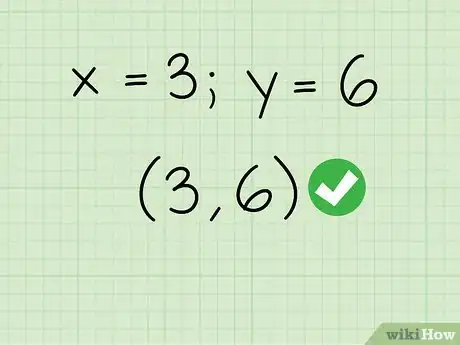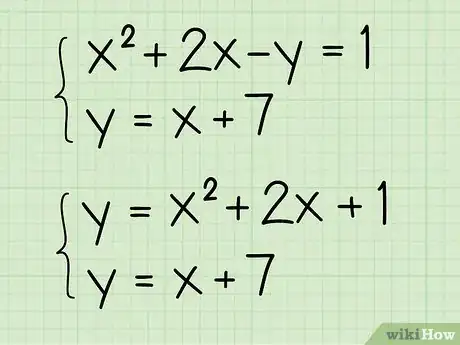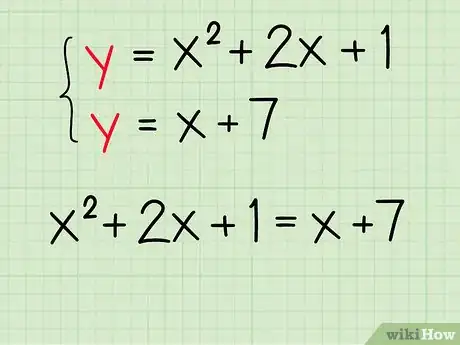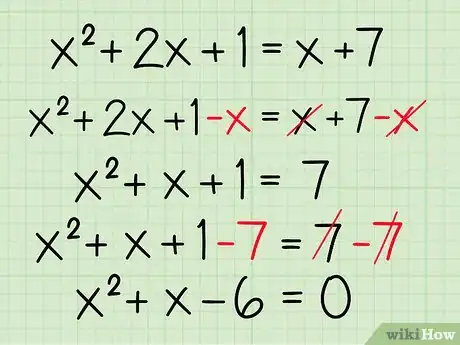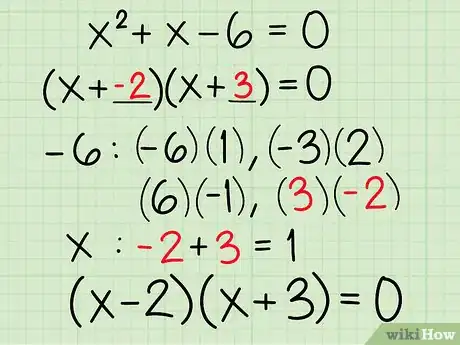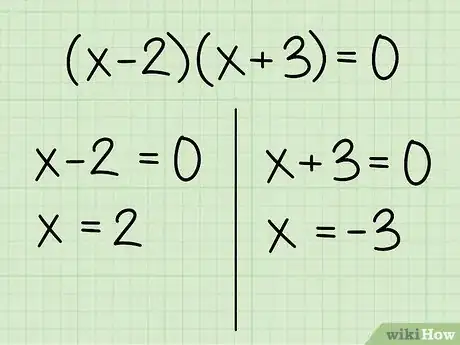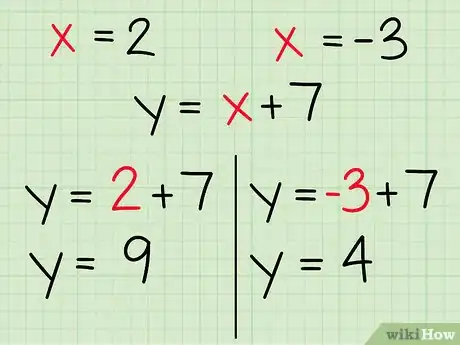Cómo encontrar algebraicamente el punto de intersección de dos líneas

Información del autor

Cuando dos líneas rectas se intersecan en un gráfico, coinciden únicamente en un punto, que se describe a través de un conjunto de coordenadas $x-$ e $y-$ . Debido a que ambas líneas pasan por ese punto, sabes que las coordenadas $x-$ e $y-$ deben satisfacer ambas ecuaciones. Con un par de técnicas adicionales, podrás encontrar las intersecciones de parábolas y otras curvas cuadráticas usando una lógica similar.

Método 1

Método 1 de 2:
Hallar la intersección de dos líneas rectas

1
Escribe la ecuación de cada una, dejando la $y$ en el lado izquierdo. Si es necesario, reordena la ecuación de modo que la variable $y$ $y$ quede sola de un lado del signo igual. Si la ecuación utiliza $f(x)$ $f(x)$ o $g(x)$ $g(x)$ en lugar de y, entonces separa ese término. Recuerda: puedes cancelar términos realizando la misma acción en ambos lados de la ecuación.
- Si no conoces las ecuaciones, encuéntralas basándote en la información que tienes.
- Ejemplo: tus dos líneas son $y=x+3$ y $y-12=-2x$ . Para despejar $y$ en la segunda ecuación, suma 12 en cada lado: $y=12-2x$
2
Establece los lados derechos de las ecuaciones iguales entre sí. Debes buscar un punto en donde las dos líneas tengan los mismos valores para $x$ $x$ e $y$ $y$ ; ahí es donde se cruzan las líneas. Ambas ecuaciones tienen solo $y$ $y$ en el lado izquierdo, así que sabes que ambos lados son iguales entre sí. Escribe una nueva ecuación que lo represente.
- Por ejemplo: sabes que $y=x+3$ y $y=12-2x$ ; por lo tanto, $x+3=12-2x$ .
3
Resuelve la ecuación para encontrar el valor de $x$ . La nueva ecuación solo tiene una variable: $x$ $x$ . Resuélvela usando álgebra, aplicando las mismas operaciones de ambos lados. Agrupa los términos de $x$ $x$ en un lado de la ecuación y luego exprésala de la forma $x$ $x$ =__ (si esto es imposible, ignora los próximos pasos y ve al final de esta sección).
- Ejemplo: $x+3=12-2x$
- Suma $2x$ en cada lado:
- $3x+3=12$
- Resta 3 en cada lado:
- $3x=9$
- Divide cada lado por 3:
- $x=3$ .
4
Utiliza este valor de $x$ para averiguar el valor de y. Elige la ecuación para cada línea. Reemplaza todas las $x$ $x$ de la ecuación por la respuesta que obtuviste. Aplica las operaciones aritméticas necesarias para resolverla y obtener el valor de $y$ $y$ .
- Ejemplo: $x=3$ y $y=x+3$
- $y=3+3$
- $y=6$
5
Revisa tu trabajo. Es una buena idea sustituir el valor de $x$ $x$ en la otra ecuación y ver si obtienes el mismo resultado. Si obtienes una solución diferente para $y$ $y$ , vuelve atrás y revisa tu trabajo para buscar el error.
- Ejemplo: $x=3$ y $y=12-2x$
- $y=12-2(3)$
- $y=12-6$
- $y=6$
- Esta es la misma respuesta que antes. Por lo tanto, sabes que no has cometido errores.
6
Escribe las coordenadas de $x$ e $y$ en la intersección. Ahora has resuelto el valor de $x$ $x$ y el valor de $y$ $y$ para el punto donde se intersecan las dos líneas. Escribe el punto como un par de coordenadas, colocando como primer número el valor de $x$ $x$ .
- Ejemplo: $x=3$ y $y=6$
- Las dos líneas se intersecan en (3,6).
7
Resuelve los casos raros. Algunas ecuaciones no permiten resolver el valor de $x$ $x$ . Esto no siempre significa que has cometido un error. Existen dos razones por las cuales un par de líneas puede producir una solución especial:
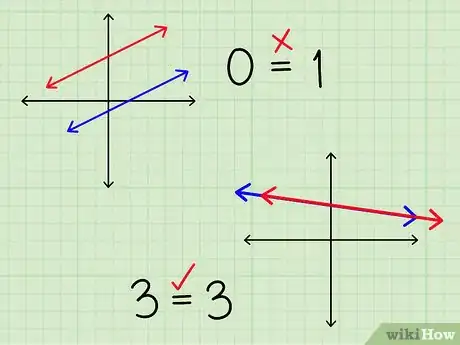
- Si las dos líneas son paralelas, no se intersecarán. Los términos de $x$ se cancelarán y tu ecuación se simplificará a una falsa declaración (por ejemplo $0=1$ ). Escribe como respuesta "las líneas no se intersecan" o "no existe solución real".
- Si las dos ecuaciones describen la misma línea, se "intersecan" en todos sus puntos. Los términos de $x$ se cancelarán y tu ecuación se simplificará a una declaración verdadera (como, por ejemplo, $3=3$ ). Escribe como respuesta "ambas ecuaciones describen la misma línea".

Método 2

Método 2 de 2:
Problemas con ecuaciones cuadráticas

1
Aprende a identificar ecuaciones cuadráticas. En una ecuación cuadrática, una o más variables están elevadas al cuadrado ( $x^{2}$ $x^{2}$ o $y^{2}$ $y^{2}$ ) y no existen potencias de nivel superior. Las líneas que representan estas ecuaciones son curvas y, por lo tanto, pueden intersecar una línea recta en 0, 1 o 2 puntos. Esta sección te enseñará cómo encontrar las 0, 1 o 2 soluciones a tu problema.
- Expande las ecuaciones con paréntesis para comprobar si son cuadráticas. Por ejemplo, $y=(x+3)(x)$ es cuadrática, ya que se expande a $y=x^{2}+3x.$
- Las ecuaciones de un círculo o de una elipse tienen un término $x^{2}$ y un término $y^{2}$ .^{[1]
  X
  Fuente de investigación}^{[2]
  X
  Fuente de investigación} Si tienes problemas con estos casos especiales, lee la sección "Consejos" más abajo.
2
Escribe las ecuaciones en términos de $y$ . Si es necesario, reescribe cada ecuación de modo que quede solo la $y$ $y$ de un lado.
- Ejemplo: encuentra la intersección de $x^{2}+2x-y=-1$ y $y=x+7$ .
- Reescribe la ecuación cuadrática en términos de $y$ :
- $y=x^{2}+2x+1$ y $y=x+7$ .
- Este ejemplo tiene una ecuación cuadrática y una ecuación lineal. Los problemas con dos ecuaciones cuadráticas se resuelven de forma similar.
3
Combina las dos ecuaciones para cancelar la $y$ . Una vez que hayas establecido ambas ecuaciones igual a $y$ $y$ , sabrás que ambos lados sin $y$ $y$ son iguales entre sí.
- Ejemplo: $y=x^{2}+2x+1$ y $y=x+7$
- $x^{2}+2x+1=x+7$
4
Ordena la nueva ecuación de modo que uno de los lados sea igual a cero. Utiliza técnicas algebraicas estándares para dejar todos los términos de un lado. Esto organizará el problema de modo que puedas resolverlo en el próximo paso.
- Ejemplo: $x^{2}+2x+1=x+7$
- Resta $x$ en cada lado:
- $x^{2}+x+1=7$
- Resta 7 en cada lado:
- $x^{2}+x-6=0$
5
Resuelve la ecuación cuadrática. Una vez que has establecido uno de los lados igual a cero, existen tres formas de resolver una ecuación cuadrática. Existen distintas opiniones acerca de cuál de ellos es más fácil. Puedes leer acerca de la fórmula cuadrática o del método de "completar el cuadrado", o seguir este ejemplo que aplica el método de factorización:
- Ejemplo: $x^{2}+x-6=0$
- El objetivo de factorizar es hallar los dos factores que multiplicados forman la ecuación. Comenzando por el primer término, sabes que $x^{2}$ puede dividirse por $x$ y $x$ . Escribe (x )(x ) = 0 para demostrarlo.
- El último término es -6. Haz una lista con cada par de factores que pueden multiplicarse para formar un 6 negativo: $-6*1$ , $-3*2$ , $-2*3$ , and $-1*6$ .
- El término del medio es $x$ (que podrías escribirlo como 1x). Suma cada par de factores hasta obtener 1 como respuesta. El par de factores correcto es $-2*3$ , debido a que $-2+3=1$ .
- Completa los espacios en blanco de tu respuesta con este par de factores: $(x-2)(x+3)=0$ .
6
Presta mucha atención, ya que puede haber dos soluciones para x. Si trabajas demasiado rápido, podrías encontrar una solución al problema y no darte cuenta de que existe una segunda. Aquí verás cómo hallar los dos valores de $x$ $x$ para las líneas que se intersecan en dos puntos:
- Ejemplo (factorización): al final obtuviste la ecuación $(x-2)(x+3)=0$ . Si cada uno de los factores entre paréntesis es igual a 0, entonces la ecuación es verdadera. Una solución es $x-2=0$ → $x=2$ . La otra solución es $x+3=0$ → $x=-3$ .
- Ejemplo (ecuaciones cuadráticas o método de completar el cuadrado): si usaste uno de estos métodos para resolver la ecuación, aparecerá una raíz cuadrada. Por ejemplo, la ecuación en este caso se convierte en $x=(-1+{\sqrt {25}})/2$ . Recuerda que una raíz cuadrada puede simplificarse a dos soluciones diferentes: ${\sqrt {25}}=5*5$ , y ${\sqrt {25}}=(-5)*(-5)$ . Escribe las dos ecuaciones, una para cada posibilidad y resuelve la $x$ para cada una de ellas.
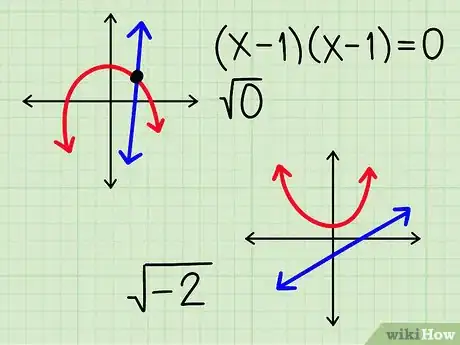
7
Resuelve problemas con una o cero soluciones. Dos líneas que apenas se tocan pueden tener una sola intersección y dos líneas que nunca se tocan pueden tener cero. A continuación, verás cómo reconocer estos casos:
- Una solución: los problemas se factorizan en dos factores idénticos ((x-1)(x-1) = 0). Al reemplazarlos en la fórmula cuadrática, el término de la raíz cuadrada es ${\sqrt {0}}$ . Solo necesitas resolver una ecuación.
- No existe solución real: no hay factores que satisfagan los requerimientos (sumando el término del medio). Cuando reemplaces los valores en la fórmula cuadrática, obtendrás un número negativo debajo del signo de raíz cuadrada (por ejemplo, ${\sqrt {-2}}$ ). Escribe como respuesta "no hay solución".
8
Reemplaza los valores de $x$ nuevamente en la ecuación original. Una vez que tengas el valor de $x$ $x$ de tu intersección, reemplázalo nuevamente en una de las ecuaciones con las cuales comenzaste. Resuélvela despejando $y$ $y$ para hallar el valor de y. Si tienes un segundo valor de x, repite este paso también para ese valor.
- Ejemplo: si encontraste dos soluciones, $x=2$ y $x=-3$ . Una de las líneas tiene la ecuación $y=x+7$ . Reemplaza $y=2+7$ y $y=-3+7$ , y luego resuelve cada ecuación para descubrir que $y=9$ y $y=4$ .
9
Escribe las coordenadas del punto. Ahora escribe tu respuesta en forma de coordenadas, con el valor de $x$ $x$ y el valor de $y$ $y$ de los puntos de intersección. Si tienes dos respuestas, asegúrate de que coincida el valor de $x$ $x$ con su correspondiente valor de y.
- Ejemplo: cuando reemplazaste $x=2$ , obtuviste $y=9$ , así que una de las intersecciones está en (2, 9). Si aplicas el mismo proceso para la segunda solución, verás que la otra intersección se encuentra en (-3, 4).

Consejos

Las ecuaciones de un círculo o una elipse tienen un término $x^{2}$ y un término $y^{2}$ . Para encontrar la intersección de un círculo y una línea recta, resuelve la ecuación lineal despejando la $x$ . Sustituye la solución de $x$ en la ecuación del círculo y obtendrás una simple ecuación cuadrática. Estos problemas pueden tener 0, 1 o 2 soluciones, tal como se explicó en el método anterior.
Los círculos y las parábolas (u otras ecuaciones cuadráticas) pueden tener 0, 1, 2, 3 o 4 soluciones. Encuentra la variable que está elevada al cuadrado en ambos términos (imagina que es x²). Resuelve despejando $x^{2}$ y sustituye la respuesta por la $x^{2}$ en la otra ecuación. Resuelve despejando $y$ para obtener 0, 1 o 2 soluciones. Reemplaza cada solución nuevamente en la ecuación cuadrática original y resuélvela para hallar el valor de $x$ . Cada una de ellas puede tener 0, 1 o 2 soluciones.