Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Las operaciones combinadas de mano de obra (o problemas de trabajo) son operaciones matemáticas que implican ecuaciones racionales.[1] Estas ecuaciones implican al menos una fracción. Las operaciones básicamente consisten en encontrar tasas unitarias, combinarlas y ponerlas en igualdad con una tasa desconocida. Estas operaciones requieren mucha lógica de interpretación, pero, siempre y cuando sepas cómo trabajar con fracciones, resolverlas es bastante sencillo.
Pasos
Método 1
Método 1 de 3:Resolver operaciones con dos personas que trabajan juntas
-
1Lee el problema detenidamente. Usa este método si el problema representa a dos o más personas que trabajan juntas para completar un trabajo. El problema también proporcionará la cantidad de tiempo que le toma a cada persona completar su trabajo por cuenta propia.
- Por ejemplo, el problema podría indicar "Si Juan puede pintar una sala en tres horas y Laura puede pintar la misma sala en cuatro horas, ¿cuánto tiempo les llevará pintar la sala juntos?".
-
2Determina la tasa horaria de cada persona. La tasa horaria está representada por la creación de una fracción, donde el número total de horas que toma completar el trabajo es el denominador (el número inferior) y uno es el numerador (el número superior).[2]
- Por ejemplo, si Juan puede pintar una sala en tres horas, su tasa horaria es de , es decir, cada hora que complete de la sala. Si Laura puede pintar la sala en cuatro horas, su tasa horaria será .
-
3Crea una proporción de la tasa horaria combinada. Esto será , donde equivale a la cantidad de tiempo que toma completar el trabajo juntos.[3]
-
4Establece la ecuación. Dado que trabajarán juntos, su tasa horaria combinada equivale a la suma de sus tasas horarias individuales.[4]
- Por ejemplo, si Juan pinta de la sala en una hora, Laura pinta de la sala en una hora, y juntos completan de la sala en una hora. La ecuación será:.
-
5Suma las fracciones. Tendrás que encontrar el mínimo denominador común. Para instrucciones completas sobre cómo sumar fracciones, puedes leer el artículo Sumar fracciones.
- Por ejemplo, 12 es el mínimo denominador común de y . Por lo tanto:
.
- Por ejemplo, 12 es el mínimo denominador común de y . Por lo tanto:
-
6Resuelve la . Para ello, haz una multiplicación cruzada. En este caso, simplemente toma la inversa de la fracción.[5]
- Por ejemplo:
.
- Por ejemplo:
-
7Simplifica la fracción, en caso de ser necesario. Esto te proporcionará la cantidad de horas que los trabajadores necesitan para completar el trabajo juntos.
- Por ejemplo, si Juan necesita tres horas para pintar una sala y Laura necesita cuatro, juntos pueden completar una sala en o de una hora. Esto equivale a casi dos horas (1 hora, 43 minutos).
Método 2
Método 2 de 3:Resolver problemas de dos personas que trabajan en contraposición
-
1Lee el problema detenidamente. Usa este método si el problema representa a una persona (o cosa) que completa un trabajo y otra persona (o cosa) que deshace el trabajo que la otra persona hace. Un problema típico implica el llenado de tuberías y el drenaje de una piscina.[6]
- Por ejemplo, el problema podría indicar "Si una manguera puede llenar una piscina en seis horas, y un drenaje abierto puede vaciarla en dos horas, ¿cuánto tomará abrir el drenaje para abrir la piscina con la manguera encendida?".
-
2Determina la tasa horaria de las personas (o cosas) que completan el trabajo. Lee el problema detenidamente para determinar cuál individuo es cuál. Si el objetivo es vaciar algo, quien se ocupe de drenar completará el trabajo. La tasa horaria está representada por la creación de una fracción, donde el número total de horas que tome completar el trabajo es el denominador (número inferior) y uno es el numerador (número superior).[7]
- Por ejemplo, si un drenaje puede vaciar una piscina en dos horas y tienes que calcular cuánto tiempo toma vaciar la piscina, el drenaje será el que complete el trabajo. Su tasa horaria es , es decir, cada hora, vacía de la piscina.
-
3Determina la tasa horaria de la persona o cosa que deshace el trabajo. Recuerda que el número total de horas que toma deshacer el trabajo estará en el denominador, y uno será el numerador.[8]
- Por ejemplo, si una manguera puede llenar una piscina en tres horas, pero el objetivo es vaciarla, la manguera será lo que deshace el trabajo. Si la manguera llena la piscina en seis horas, su tasa horaria será ; es decir, cada hora, llena de la piscina.
-
4Crea una proporción de la tasa horaria combinada. Esto será , donde equivale a la cantidad de tiempo que les toma completar el trabajo mientras trabajan en contraposición.[9]
-
5Establece la ecuación. Dado que trabajarán en contraposición, su tasa horaria combinada equivale a la diferencia entre sus tasas horarias individuales.[10] Esta es la tasa horaria de la persona o cosa que completa el trabajo menos la tasa horaria de la persona o cosa que deshace el trabajo.
- Por ejemplo, si el drenaje vacía de una piscina en una hora, una manguera llena de una piscina en una hora, y juntos vacían de una piscina en una hora, la ecuación será:.
-
6Resta las fracciones. Tendrás que encontrar el mínimo denominador común. Para instrucciones completas sobre cómo restar fracciones, puedes leer el artículo Restar fracciones.
- Por ejemplo, 6 es el mínimo denominador común de y . Por lo tanto:
.
- Por ejemplo, 6 es el mínimo denominador común de y . Por lo tanto:
-
7Haz una multiplicación cruzada para resolver . Ten en cuenta que, en este caso, puedes simplemente tomar la inversa de la fracción.[11]
- Por ejemplo,
.
- Por ejemplo,
-
8Simplifica la fracción, en caso de ser necesario. Esto te proporcionará la cantidad de horas que les toma a las personas o cosas completar el trabajo mientras trabajan en contraposición.
- Por ejemplo, si una manguera llena una piscina en seis horas y el drenaje la vacía en dos horas, trabajando en contraposición, la piscina se drenará en horas o horas.
Método 3
Método 3 de 3:Resolver problemas con dos personas que trabajan por turno
-
1Lee el problema detenidamente. Usa este método si el problema representa a dos o más personas (o cosas) que trabajan juntas para completar un trabajo por una parte del tiempo, y luego solo una persona (o cosa) completa (o termina) el trabajo por cuenta propia. El problema también debe proporcionar la tasa horaria de cada persona.
- Por ejemplo, el problema podría ser: "Nicolás puede limpiar el refugio para gatos en ocho horas y María puede limpiarlo en cuatro horas. Trabajan juntos por dos horas, pero María se marcha para llevar a algunos gatos al veterinario. ¿Cuánto tiempo le tomará a Nicolás terminar de limpiar el refugio solo?".
-
2Determina la tasa horaria de cada persona. La tasa horaria está representada por la creación de una fracción, donde el número total de horas que tome completar el trabajo es el denominador (número inferior) y uno es el numerador (número superior).[12]
- Por ejemplo, si Nicolás puede limpiar el refugio para gatos en ocho horas, su tasa horaria es ; es decir, cada hora, completa de una sala. Si María necesita cuatro horas para limpiar el refugio, su tasa horaria será .
-
3Determina cuánto pueden completar juntos en una hora. Para ello, suma sus tasas horarias. Para instrucciones completas sobre cómo sumar fracciones, lee el artículo Sumar fracciones.
- Por ejemplo, si Nicolás limpia de una sala en una hora y María completa de la sala en una hora, juntos completan de la sala en una hora:
- Por ejemplo, si Nicolás limpia de una sala en una hora y María completa de la sala en una hora, juntos completan de la sala en una hora:
-
4Calcula cuánto completan los trabajadores juntos. Para ello, multiplica cuánto completan por hora por la cantidad de horas que trabajan juntos.[13] Para instrucciones completas sobre cómo multiplicar fracciones, lee el artículo Multiplicar fracciones.
- Por ejemplo, si Nicolás y María juntos limpian del refugio en una hora, en dos horas, completarán el doble:
del refugio.
- Por ejemplo, si Nicolás y María juntos limpian del refugio en una hora, en dos horas, completarán el doble:
-
5Calcula cuánto trabajo resta después de que cada persona se marcha. Para ello, resta la fracción de lo que han hecho por 1 entero. Para instrucciones completas sobre cómo restar fracciones, lee el artículo Restar fracciones.
- Por ejemplo, si Nicolás y María limpian del refugio en dos horas, después de que María se marcha, Nicolás tiene que limpiar del refugio solo.
-
6Establece la ecuación. Ahora, calcula cuánto le tomará a cada persona restante completar el trabajo. Para ello, multiplica la tasa horaria de cada uno por la cantidad de horas () que tomará completar el trabajo. Esto equivale a la cantidad de trabajo que se debe terminar.[14]
- Por ejemplo, si Nicolás limpia el refugio a una tasa de por hora y tiene que completar del trabajo solo, la ecuación será , o, más simple,
-
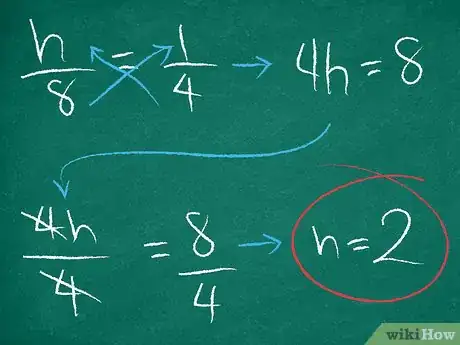
7Resuelve la . Para ello, haz una multiplicación cruzada de las dos fracciones. Asegúrate de simplificarlas, en caso de ser necesario. Esto te proporcionará la cantidad de horas que le tomará a la persona restante completar el trabajo por cuenta propia.
- Por ejemplo:
Por lo tanto, Nicolás necesitará dos horas para completar el trabajo solo.
- Por ejemplo:
Consejos
- Presta mucha atención a las unidades. Estos métodos funcionan para cualquier unidad de tiempo, como minutos o días. Algunas operaciones pueden establecer las tasas en distintas unidades, y tendrás que convertirlas.
- Si la operación implica a más de dos trabajadores, simplemente suma sus tasas de trabajo individuales. Luego, toma el recíproco de la suma para obtener el tiempo que toma trabajar juntos.
Cosas que necesitarás
- una calculadora
Referencias
- ↑ http://www.mathguide.com/lessons/Word-Work.html
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Algebra_WorkingTogether.xml
- ↑ http://purplemath.com/modules/workprob.htm
- ↑ http://purplemath.com/modules/workprob.htm
- ↑ http://purplemath.com/modules/workprob.htm
- ↑ http://purplemath.com/modules/workprob2.htm
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Algebra_WorkingTogether.xml
- ↑ http://www.algebralab.org/Word/Word.aspx?file=Algebra_WorkingTogether.xml
- ↑ http://purplemath.com/modules/workprob2.htm











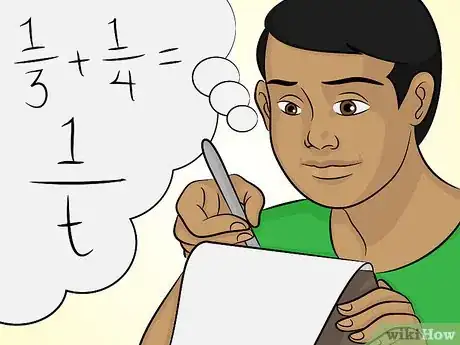

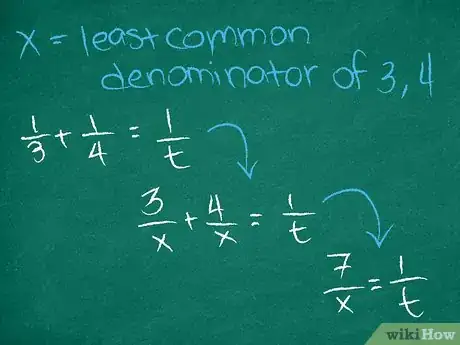





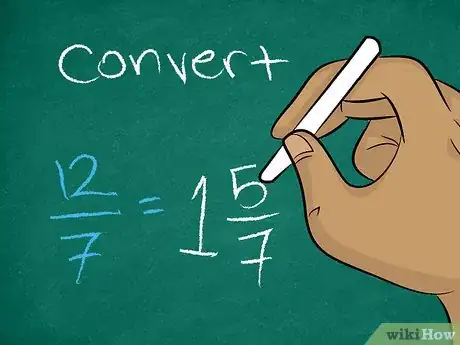






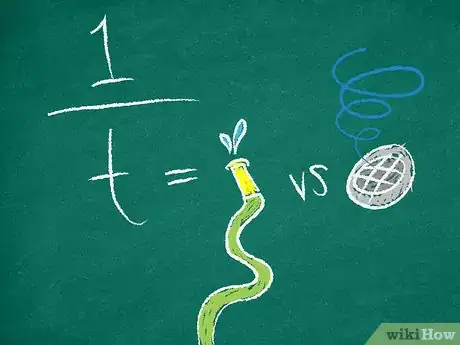


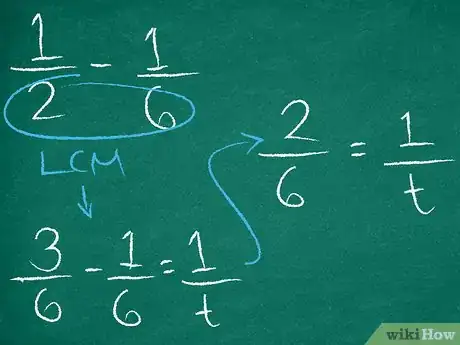


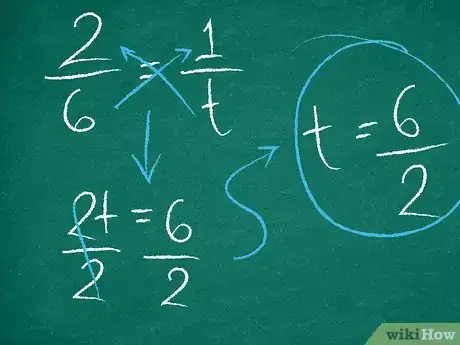


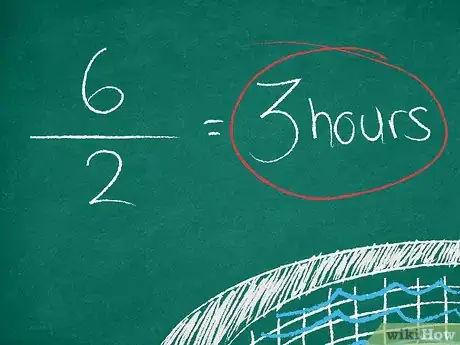





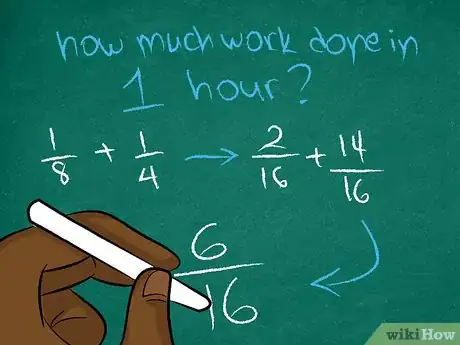



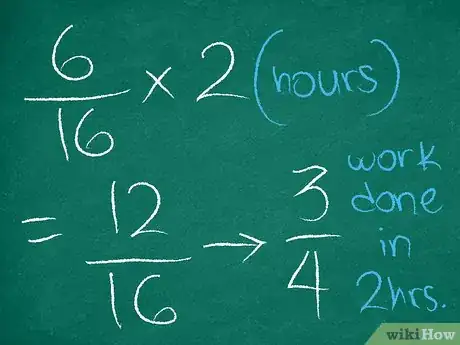




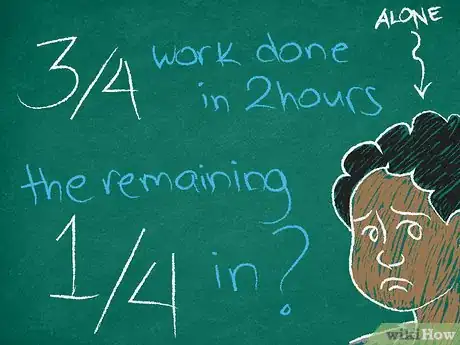


























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.