Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
En este artículo, hay 8 referencias citadas, que se pueden ver en la parte inferior de la página.
Este artículo ha sido visto 18 484 veces.
Las expresiones racionales son expresiones en forma de una fracción (o razón) de dos polinomios.[1] Así como con las fracciones regulares, una expresión racional se puede simplificar. Este es un proceso muy simple si el factor es un monomio (o factor de un solo término); sin embargo, puede ser un poco más detallado si el factor incluye varios términos.
Pasos
Método 1
Método 1 de 3:Factorizar monomios
-
1Analiza la expresión. Para usar este método debes ubicar un monomio en el numerador y en el denominador de tu expresión racional. Un monomio es un polinomio con un término.[2]
- Por ejemplo, la expresión tiene un término en el numerador y otro término en el denominador. Por lo tanto, cada uno es un monomio.
- La expresión tiene dos binomios y, por lo tanto, no se puede resolver mediante este método.
-
2Factoriza el numerador. Para hacerlo, escribe los factores que multiplicarías para obtener el monomio, incluyendo la variable. Para más información sobre cómo factorizar, lee este artículo sobre cómo factorizar un número. Vuelve a escribir la expresión usando los factores en el numerador y denominador.[3]
- Por ejemplo, lo factorizarías como y como . Por lo tanto, luego de factorizar la expresión se vería así:
- Por ejemplo, lo factorizarías como y como . Por lo tanto, luego de factorizar la expresión se vería así:
-
3Cancela los factores que compartan el numerador y denominador. Para hacerlo, tacha los factores que coincidan. La cancelación se da porque divides un factor entre sí mismo, lo cual es igual a 1.[4]
- Por ejemplo, en el numerador y denominador puedes tachar dos “2” y una “x” y la expresión quedaría así:
- Por ejemplo, en el numerador y denominador puedes tachar dos “2” y una “x” y la expresión quedaría así:
-
4Vuelve a escribir la expresión con los factores restantes. Recuerda que los términos que se cancelan dan 1 como resultado. Por lo tanto, si has cancelado todos los términos en el numerador o denominador, todavía te quedará “1”.
- Por ejemplo:
- Por ejemplo:
-
5Termina toda multiplicación que haya en el numerador o denominador. Así obtendrás la expresión racional, simplificada y final.
- Por ejemplo:
- Por ejemplo:
Método 2
Método 2 de 3:Factorizar factores comunes monomios
-
1Analiza la expresión racional. Para usar este método debes ubicar al menos un binomio en tu expresión. Puede ser en el numerador, denominador o en ambos. Un binomio es un polinomio con dos términos.[5]
- Por ejemplo, la expresión tiene dos términos en el denominador. Por lo tanto, este contiene un binomio.
-
2Encuentra un factor monomio que sea común para el numerador y denominador. El factor debe ser común para todos los términos de la expresión. Factoriza dicho término y vuélvelo a escribir en la expresión.[6]
- Por ejemplo, el monomio es común a cada término de la expresión . Por lo tanto, después de factorizar dicho término del numerador y denominador, la expresión se verá así:
- Por ejemplo, el monomio es común a cada término de la expresión . Por lo tanto, después de factorizar dicho término del numerador y denominador, la expresión se verá así:
-
3Cancela el factor común. Al factorizar los monomios del numerador y denominador obtienes 1 ya que estarás dividiendo dicho término entre sí mismo.[7]
- Por ejemplo:
- Por ejemplo:
-
4Vuelve a escribir la expresión después de cancelar el monomio. Así obtendrás la expresión racional simplificada. Si lo factorizaste de manera correcta, no habrá factores que sean comunes a cada término del numerador y denominador.
- Por ejemplo:
- Por ejemplo:
Método 3
Método 3 de 3:Factorizar factores comunes binomios
-
1Analiza la expresión. Este método funciona con las expresiones que tienen polinomios de segundo grado en el numerador y denominador. Un polinomio de segundo grado es uno que tiene un término elevado a la potencia 2.[8]
- Por ejemplo, la expresión tiene un polinomio de segundo grado en el numerador y denominador; por lo tanto, puedes utilizar este método para simplificarlo.
-
2Factoriza el polinomio del numerador en dos binomios. Aquí lo que harás será buscar dos binomios que te den el polinomio original al multiplicarlos por el método FOIL. Para más información sobre la manera de factorizar un polinomio de segundo grado, lee este artículo. Vuelve a escribir la expresión con el numerador factorizado.
- Por ejemplo, se puede factorizar como . Por lo tanto, ahora la expresión se vería así:
- Por ejemplo, se puede factorizar como . Por lo tanto, ahora la expresión se vería así:
-
3Factoriza el polinomio del denominador en dos binomios. Una vez más, lo que harás será buscar dos binomios que te den el polinomio original al multiplicarlos. Vuelve a escribir la expresión con el denominador factorizado.
- Por ejemplo, se puede factorizar como . Por lo tanto, ahora la expresión se vería así:
- Por ejemplo, se puede factorizar como . Por lo tanto, ahora la expresión se vería así:
-
4
-
5Vuelve a escribir la expresión con los factores restantes. Recuerda que te quedará 1 si cancelas todos los factores. Así obtendrás la expresión simplificada y final.
- Por ejemplo:
- Por ejemplo:
Cosas que necesitarás
- calculadora
- lápiz
- papel
Referencias
- ↑ https://www.mathsisfun.com/algebra/rational-expression.html
- ↑ https://www.mathsisfun.com/definitions/monomial.html
- ↑ https://www.youtube.com/watch?v=nVri1tpH3cI
- ↑ http://www.purplemath.com/modules/rtnldefs2.htm
- ↑ https://www.mathsisfun.com/definitions/binomial.html
- ↑ https://www.khanacademy.org/math/algebra2/rational-expressions-equations-and-functions/simplify-rational-expressions/v/simplifying-rational-expressions-w-common-monomial-factors
- ↑ http://www.purplemath.com/modules/rtnldefs2.htm
- ↑ http://www.purplemath.com/modules/polydefs.htm
- ↑ http://tutorial.math.lamar.edu/Classes/Alg/RationalExpressions.aspx




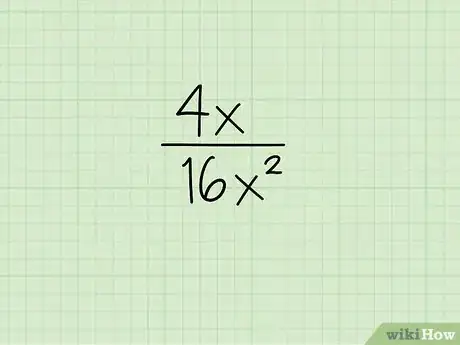


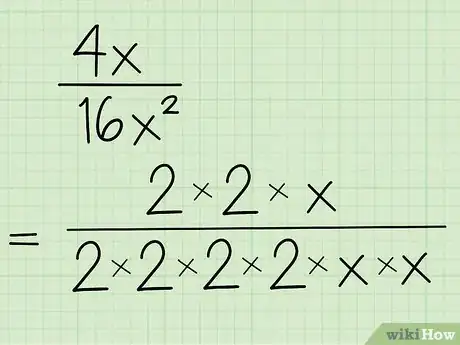









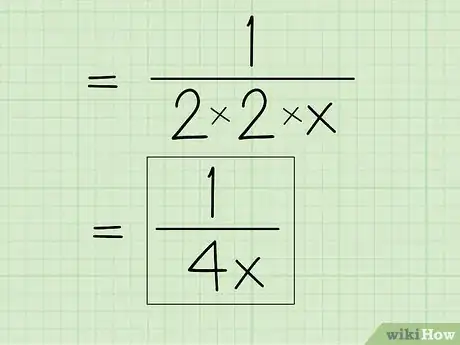

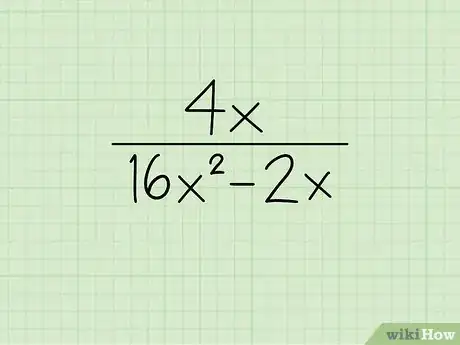

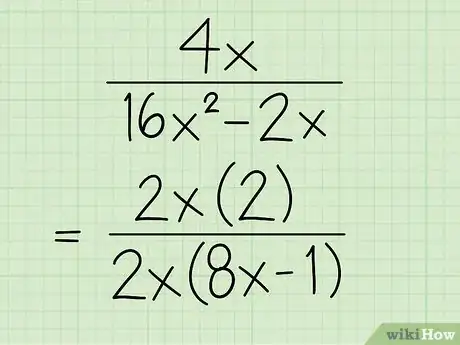


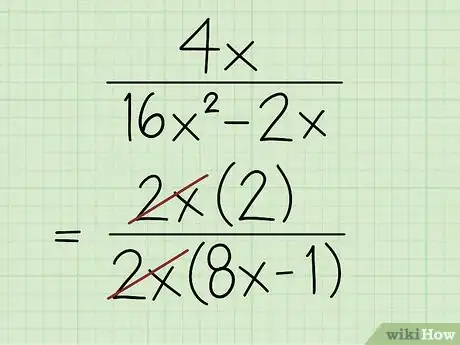

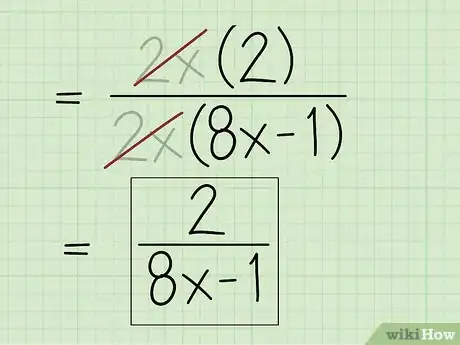

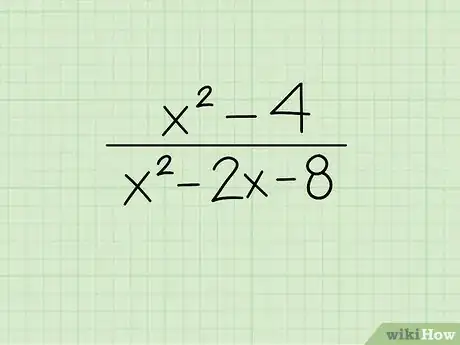

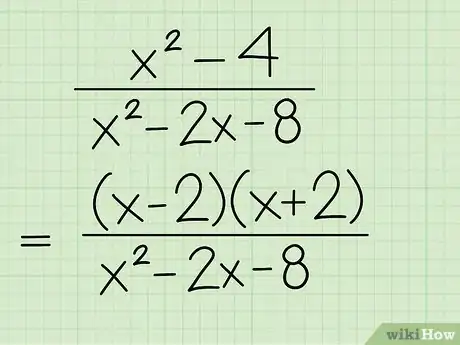



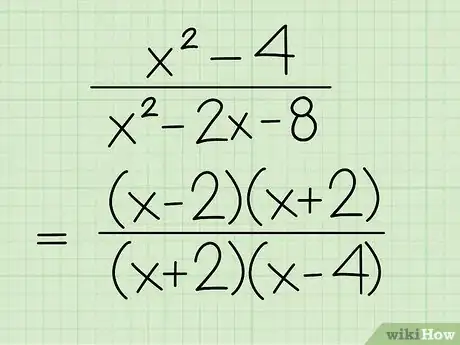



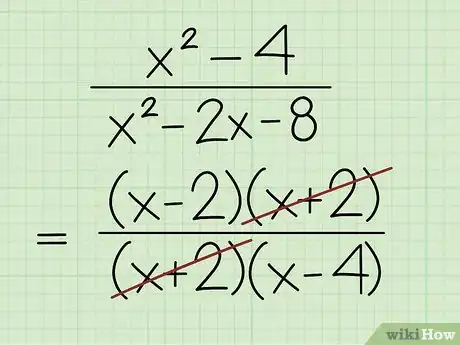

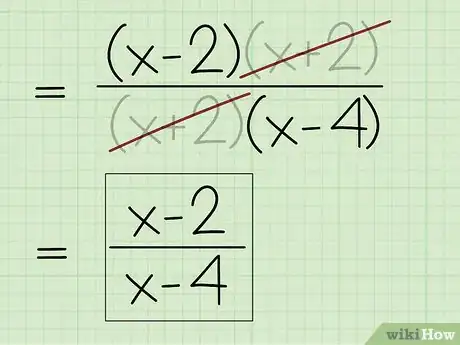




















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 18 484 veces.