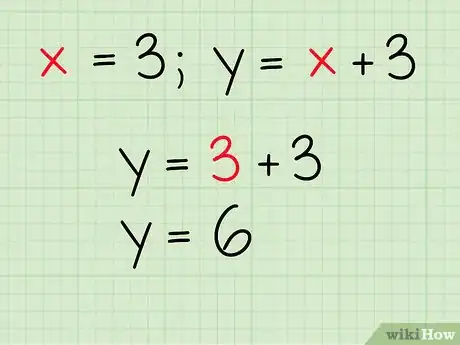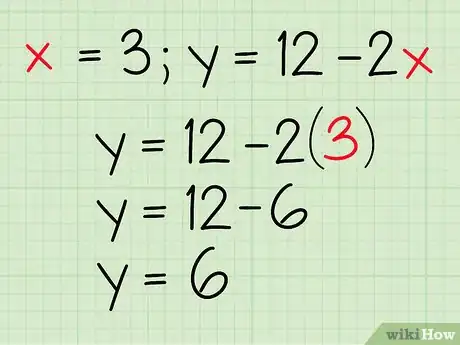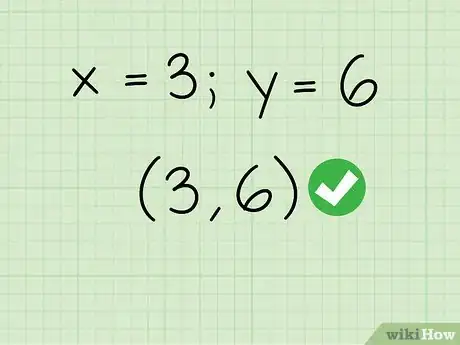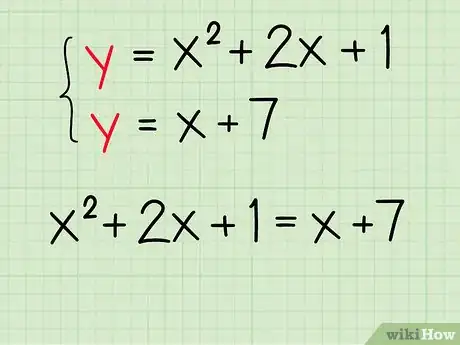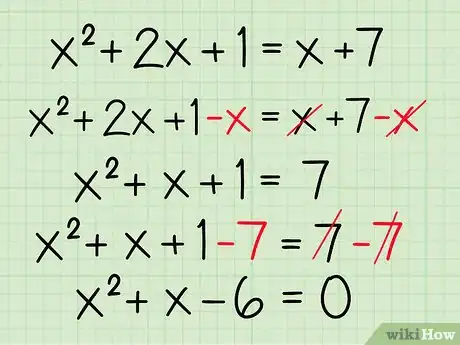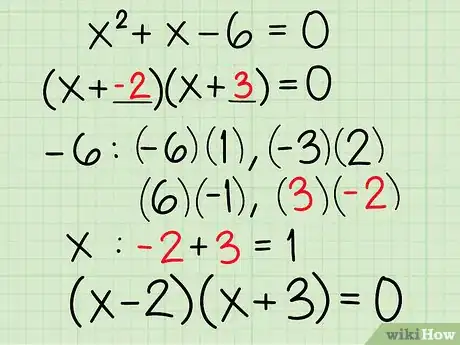Comment déterminer algébriquement le point d'intersection de deux courbes

Informations concernant l'auteur.e

Dans un repère orthonormé à deux dimensions, quand deux droites non parallèles se coupent, c'est forcément en un seul point de coordonnées (x,y). Partant de ce constant, ces dernières satisfont obligatoirement les équations des droites. Trouver ce point est assez facile. De la même façon, il est possible de trouver les coordonnées du point d'intersection avec des graphes comme ceux de paraboles ou des hyperboles.

Méthode 1

Méthode 1 sur 2:
Trouver l'intersection de deux droites

1
Notez les deux équations l'une sous l'autre. Faites en sorte que le y soit à gauche. Si ce n'est pas déjà fait, arrangez-vous pour que y soit à cette place. Il est possible qu'on vous donne la fonction soit la forme f(x) = ax + b : ce n'est pas grave, ce f(x) doit être à gauche, il remplace y en fait. Pour rappel, toute opération effectuée dans un des membres doit l'être dans l'autre.
- Si l'équation (ou les deux) ne vous est pas donnée, vous devrez la trouver à partir des données que vous aurez.
- Exemple : prenons deux droites d'équations $y=x+3$ et $y-12=-2x$ . Transformez la seconde en ajoutant 12 de chaque côté de l'équation, ce qui donne : $y=-2x+12$
2
Mettez les deux membres de droite à égalité. Le but est de trouver les coordonnées du point d'intersection de deux droites : elles se coupent donc en un seul point. Comme y = y, forcément les deux autres membres sont égaux. C'est pourquoi on les met à égalité pour déterminer x.
- Exemple : en reprenant les deux équations $y=x+3$ et $y=-2x+12$ , cela donne : $x+3=-2x+12$ .
3
Calculez x. La nouvelle équation n'a qu'une seule inconnue : x. Sa résolution consiste à isoler les x d'un côté et les valeurs numériques de l'autre, ce qui vous donnera finalement quelque chose de la forme x = __. Si ce n'est pas possible, passez à cette étape.
- Exemple : $x+3=-2x+12$
- Ajoutez $2x$ de chaque côté
- $3x+3=12$
- Ôtez 3 de chaque côté
- $3x=9$
- Divisez par 3 de chaque côté
- $x=3$
4
Servez-vous de x pour calculer y. Prenez l'une quelconque des équations de départ et remplacez le x par la valeur que vous venez de trouver. Faites les calculs et vous trouverez y.
- Exemple : $x=3$ et $y=x+3$
- $y=3+3$
- $y=6$
5
Vérifiez vos calculs. Pour vérifier que vous avez la bonne réponse, faites les mêmes calculs avec la seconde équation. Si vous ne vous êtes pas trompé, vous devriez trouver la même valeur pour y. Si ce n'est pas le cas, c'est que vous vous êtes trompés dans ce dernier calcul ou dans le calcul de x.
- Exemple : $x=3$ et $y=-2x+12$
- $y=-2(3)+12$
- $y=-6+12$
- $y=6$
- Les deux calculs coïncident : vous n'avez pas fait d'erreurs.
6
Inscrivez les coordonnées (x,y) du point d'intersection. Vous avez à présent l'abscisse (x) et l'ordonnée (y) du point d'intersection de vos deux droites. Rédigez la réponse en entier en mettant les deux coordonnées entre parenthèses, l'abscisse étant notée en premier.
- Exemple : $x=3$ et $y=6$
- Les deux droites ont un seul point d'intersection en (3,6).
7
Sachez que faire en cas de résultats bizarres. Il arrive que vous ne puissiez pas trouver les coordonnées du point d'intersection, sans que vous vous soyez trompé pour autant. Il existe deux cas de figure qui aboutissent à une solution particulière.
- Si les deux droites sont parallèles, elles ne peuvent pas, par définition, avoir de point d'intersection. Les deux droites ont le même coefficient directeur qui s'annule donc quand on pose l'égalité des équations, vous obtenez alors quelque chose du genre : $0=1$ , ce qui est évidemment faux. Comme réponse, vous pouvez inscrire que ces deux droites ne se coupent pas ou qu'il n'y a pas de solution réelle au problème.
- Si les deux équations ne sont en fait qu'une seule et même équation, sous deux formes différentes, en ce cas, comme c'est la même droite, elles ont une quantité infinie de points d'intersection. Quand vous les mettez à égalité, les x s'annulent et vous vous retrouvez avec une égalité toujours vérifiée, du genre $3=3$ . La seule réponse à ce problème est que les deux droites ne sont qu'une et que tous les points sont des points d'intersection.
Publicité

Méthode 2

Méthode 2 sur 2:
Trouver l'intersection de deux graphes de fonctions du second degré

1
Sachez reconnaitre une fonction du second degré. Dans une telle fonction, un des termes, souvent x, est au carré ( $x^{2}$ $x^{2}$ , éventuellement on a $y^{2}$ $y^{2}$ ). Aucun terme n'a une puissance supérieure à 2. Le graphe d'une telle fonction est une parabole, un cercle ou une ellipse, ce qui fait qu'avec une droite, il peut y avoir zéro, un ou encore deux points d'intersection. Il faut envisager ces trois cas de figure.
- Vérifiez que la fonction est bien du second degré. Si la fonction est factorisée, il est parfois difficile de savoir si c'est bien une fonction du second degré. Ainsi, $y=(x+3)(x)$ est une équation du second degré, car une fois développée, elle se présente sous la forme : $y=x^{2}+3x.$
- Quand une fonction présente les termes $x^{2}$ et $y^{2}$ , vous pouvez être sûr que c'est un cercle ou une ellipse ^{[1]
  X
  Source de recherche} ^{[2]
  X
  Source de recherche}. Pour plus de renseignements sur ces courbes spéciales, reportez-vous à la partie Conseils se trouvant à la fin de cet article.
2
Notez les deux équations l'une sous l'autre. Comme précédemment, faites en sorte que le y soit à gauche, il est parfois nécessaire de réorganiser la fonction.
- Exercice : trouvez le point d'intersection de la courbe $x^{2}+2x-y=-1$ et de la droite $y=x+7$ .
- Réorganisez la première fonction en isolant y à gauche.
- Vous obtenez ainsi : $y=x^{2}+2x+1$ et $y=x+7$ .
- Cet exemple comporte donc une fonction du second degré et une fonction linéaire. Avec deux fonctions du second degré, le raisonnement serait le même.
3
Mettez les deux membres de droite à égalité. Comme y = y, forcément les deux autres membres sont égaux et y a disparu, il ne reste qu'une seule inconnue : x.
- Exemple : $y=x^{2}+2x+1$ et $y=x+7$
- $x^{2}+2x+1=x+7$
4
Arrangez l'équation pour qu'il y ait 0 d'un côté. Il vous faut à présent arranger l'équation pour que le membre de droite soit égal à 0. Pour cela, vous devez respecter certaines règles d'algèbre, comme celle qui veut qu'une opération faite sur un membre le soit sur l'autre.
- Exemple : $x^{2}+2x+1=x+7$
- Soustrayez x des deux côtés
- $x^{2}+x+1=7$
- Soustrayez 7 des deux côtés
- $x^{2}+x-6=0$
5
Résolvez l'équation du second degré. Votre équation est désormais égale à 0, vous avez à votre disposition trois façons de procéder pour la résoudre, c'est-à-dire trouver x : la méthode par le déterminant, celle consistant à compléter le carré ou celle qui consiste à factoriser.
- Exemple : $x^{2}+x-6=0$
- Factoriser une équation consiste en fait à trouver un produit de monômes, et donc deux racines. Ainsi, $x^{2}+x-6=0$ peut se décomposer de la façon suivante : (x + a)(x + b) = 0, a et b étant les racines.
- Le dernier terme est -6. Dressez la liste de toutes les paires de facteurs qui ont pour produit -6. Il y a : $-6\times 1$ , $-3\times 2$ , $-2\times 3$ et $-1\times 6$ .
- Le terme du milieu est x (que nous écrirons 1x). Trouvez la paire de facteurs dont la somme est égale à 1. Une seule paire répond à cette condition et c'est $-2\times 3$ ( $-2+3=1$ ).
- Remplacez a et b par ces deux racines de l'équation, ce qui vous donne : $(x-2)(x+3)=0$ .
6
Pensez qu'il y a toujours deux solutions. Il peut arriver qu'il n'y ait qu'une solution (c'est une identité remarquable), mais le plus souvent, il y a deux solutions. C'est bien d'avoir une racine, mais il en faut deux. Cela signifie qu'il y a deux points d'intersection entre la parabole et la droite linéaire.
- Dans notre exemple de factorisation, nous avons désormais le produit suivant : $(x-2)(x+3)=0$ . Il suffit qu'un des deux éléments de l'équation soit égal à 0 pour que l'équation soit satisfaite. Posons donc $x-2=0$ , soit $x=2$ , puis posons que $x+3=0$ , soit $x=-3$ .
- Avec la méthode du déterminant, vous auriez trouvé deux racines, à savoir : $x=(-1+{\sqrt {25}})/2$ et $x=(-1-{\sqrt {25}})/2$ (partant du principe qu'un nombre et son opposé donnent le même carré). Une fois les calculs opérés, vous auriez trouvé : $x=(-1+5)/2$ et $x=(-1-5)/2$ , soit $x=(4)/2=2$ et $x=(-1-5)/2=-6/2=-3$ .
7
Sachez qu'il existe des cas avec une seule solution ou aucune. Cela se produit quand la droite est tangente à la parabole (un seul point d'intersection) ou quand les courbes ne se rencontrent jamais sans être parallèles (aucun point d'intersection).
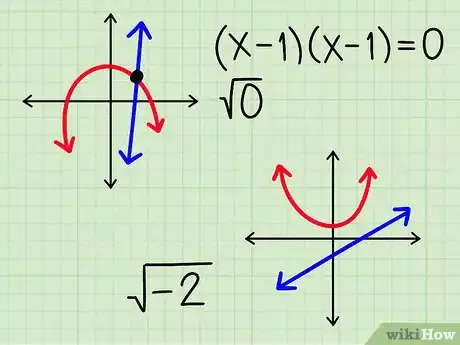
- Il n'y a qu'une seule solution quand l'équation est une certaine identité remarquable, du type (x-1)(x-1) = 0, il n'y a qu'un seul point d'intersection. L'équation a certes deux racines, mais elles sont identiques, à savoir 1 : un seul point d'intersection donc.
- Il n'y a aucune solution quand la quantité qui, dans le déterminant, se trouve sous le signe de la racine est négative (comme ${\sqrt {-2}}$ ). En ce cas, vous inscrirez comme réponse que les deux graphes ne se coupent pas et n'ont donc aucun point d'intersection.
8
Servez-vous des x pour calculer les y. Prenez l'une quelconque des équations de départ et remplacez le x par une des valeurs que vous venez de trouver. Faites les calculs et vous trouverez y. S'il y a deux points d'intersection, faites la même chose avec la seconde valeur de x.
- Exemple : nous avons trouvé deux solutions, à savoir $x=2$ et $x=-3$ . Une des droites ayant pour équation $y=x+7$ , il suffit de remplacer x par 2, puis par -3, ce qui donne : $y=2+7$ et $y=-3+7$ . Après avoir fait les calculs, on a respectivement : $y=9$ et $y=4$ .
9
Présentez correctement vos réponses. Indiquez les deux points d'intersection avec leurs coordonnées sous la forme (x,y). Faites attention à ne pas mélanger les coordonnées. S'il n'y a qu'un point, vous ne risquez pas de vous tromper.
- Exemple : avec $x=2$ , nous avons obtenu $y=9$ , ce qui signifie qu'il y a un premier point d'intersection en (2, 9). Dans la même veine, avec $x=-3$ , nous avons un second point d'intersection en (-3, 4).
Publicité

Conseils

Dans l'équation d'un cercle ou d'une ellipse, il y a toujours un terme au deuxième degré $x^{2}$ et un autre terme au même degré, $y^{2}$ . Dans le cas d'une intersection d'un cercle et d'une droite, le mieux est de trouver x avec l'équation de la droite. Ensuite seulement, vous déterminerez y avec l'équation du cercle, ce ne sera alors qu'une simple équation du second degré à résoudre. Il peut y avoir, dans ce cas précis, un ou deux points d'intersection… mais aussi aucun.
Un cercle et une parabole peuvent avoir 0, 1, 2, 3 ou 4 points d'intersection. En ce cas, il faut trouver la valeur de la variable au carré, disons pour faire simple, $x^{2}$ . Remplacez le $x^{2}$ de l'autre équation par la valeur que vous venez de trouver. Faites les calculs et vous trouverez pour y une ou deux solutions… ou aucune. Cela fait, remplacez dans une des deux équations y par sa ou ses valeurs. Après avoir fait tous les calculs, vous trouverez pour x à nouveau une ou deux solutions… ou aucune.