Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 106 533 veces.
Si sabes multiplicar dos matrices, ya estás bien encaminado hacia "dividir" una matriz entre otra. Esa palabra está entre comillas porque las matrices técnicamente no pueden dividirse. En cambio, se multiplica una matriz por la inversa de otra. Si esto suena extraño, considéralo en términos de una matemática que te sea más familiar: en lugar de calcular 10 ÷ 5, podemos tomar la inversa de 5 (5-1 o 1/5), resolver 10 x 5-1 y terminar con la misma respuesta. Por eso es que multiplicar por la inversa de una matriz se considera el proceso más cercano a la división definido en esta rama de las matemáticas. Estos cálculos se utilizan comúnmente para resolver sistemas de ecuaciones lineales.[1]
Resumen rápido
- No existe una definición para la división de matrices. En cambio, multiplica la primera matriz por la inversa de la segunda. Reescribe el problema [A] ÷ [B] como [A] * [B]-1 o [B]-1 * [A].
- Si la matriz [B] no es cuadrada o si su determinante es 0, escribe "no hay una única solución". De otro modo, encuentra el determinante de [B] y pasa al siguiente paso.
- Encuentra [B]-1 (la inversa de [B]).
- Multiplica las matrices para encontrar [A] * [B]-1 o [B]-1 * [A]. Ten en cuenta que estas no necesariamente darán la misma respuesta.
Pasos
Parte 1
Parte 1 de 3:Confirmar que la "división" es posible
-
1Comprende la "división" de matrices. Técnicamente, no existe la división de matrices. Dividir una matriz entre otra es una función indefinida.[2] El equivalente más cercano es multiplicar por la inversa de otra matriz. En otras palabras, mientras que [A] ÷ [B] es indefinido, puedes resolver el problema [A] * [B]-1. Debido a que estas dos ecuaciones serían equivalentes si utilizaras cantidades escalares, esto parece una división de matrices pero es importante utilizar la terminología correcta.
- Ten en cuenta que [A] * [B]-1 y [B]-1 * [A] no son el mismo problema. Quizás tengas que resolver ambos para encontrar todas las soluciones posibles.
- Por ejemplo, en lugar de , escribe .
Quizás también tengas que calcular , las cuales podrían tener una respuesta diferente.
-
2Confirma que la "matriz divisora" es cuadrada. Para obtener la inversa de una matriz, debe ser una matriz cuadrada con el mismo número de filas y columnas. Si la matriz que planeas invertir no es cuadrada, no habrá una única solución al problema.[3]
- El término "matriz divisora" es un poco vago ya que no es técnicamente un problema de división. Para [A] * [B]-1, esto se refiere a la matriz [B]. En nuestro problema de ejemplo, esta es .
- A una matriz que tenga una inversa se le llama "invertible" o "no singular". Las matrices que no tienen una inversa son "singulares".
-
3Verifica que ambas matrices puedan multiplicarse. Para multiplicar dos matrices, la cantidad de columnas en la primera matriz debe ser igual a la cantidad de filas en la segunda.[4] Si esto no funciona en cualquiera de las disposiciones ([A] * [B]-1 o [B]-1 * [A]), no hay una solución al problema.
- Por ejemplo, si [A] es una matriz de 4 x 3 y [B] es una matriz de 2 x 2, no hay una solución. [A] * [B]-1 no funciona porque 4 ≠ 2 y [B]-1 * [A] no funciona porque 2 ≠ 3.
- Ten en cuenta que la inversa [B]-1 siempre tiene el mismo número de filas y columnas que la matriz original [B]. No necesitas calcular la inversa para terminar este paso.
- En nuestro ejemplo, ambas matrices son de 2 x 2, así que pueden multiplicarse en cualquier orden.
-
4Encuentra el determinante de una matriz de 2 x 2. Hay un requisito más que debes revisar antes de poder encontrar la inversa de una matriz. El determinante de la matriz no debe ser cero. Si el determinante es cero, la matriz no tiene una inversa. Así es como puedes encontrar el determinante en el caso más simple, una matriz de 2 x 2:
- Matriz de 2 x 2: el determinante de la matriz es ad - bc. En otras palabras, resta el producto de la diagonal principal (de la esquina superior izquierda hacia la esquina inferior derecha) al producto de la antidiagonal (de la esquina superior derecha hacia la esquina inferior izquierda).
- Por ejemplo, la matriz tiene el determinante (7)(3) - (4)(2) = 21 - 8 = 13. Este no es cero, así que es posible encontrar la inversa.
-
5Encuentra el determinante de una matriz más grande. Si la matriz es de 3 x 3 o más grande, encontrar el determinante toma un poco más de trabajo:
- Matriz de 3 x 3: elige cualquier elemento y tacha la fila y la columna a la que pertenezca. Encuentra el determinante de la matriz restante de 2 x 2, multiplica por el elemento elegido y consulta un cuadro de signos de matrices para determinar el signo. Repite el procedimiento para los otros dos elementos de la misma fila o columna que el primero que hayas elegido y luego suma los tres determinantes. Lee este artículo para obtener instrucciones paso a paso y consejos sobre cómo acelerar este proceso.
- Matrices más grandes: se recomienda usar una calculadora o software gráfico. El método es similar al método para las matrices de 3 x 3 pero es tedioso hacerlo a mano.[5] Por ejemplo, para encontrar el determinante de una matriz de 4 x 4, tienes que encontrar los determinantes de cuatro matrices de 3 x 3.
-
6Continúa. Si la matriz no es cuadrada o si el determinante es cero, escribe "no hay una única solución ". El problema está terminado. Si la matriz es cuadrada y su determinante no es cero, pasa a la siguiente sección para el siguiente paso: encontrar la inversa.
Parte 2
Parte 2 de 3:Invertir la matriz
-
1Cambia las posiciones de los elementos de la diagonal principal de la matriz 2 x 2. Si la matriz es de 2 x 2, puedes usar un atajo para facilitar mucho más este cálculo.[6] El primer paso de este atajo involucra cambiar el elemento de la esquina superior izquierda con el de la esquina inferior derecha. Por ejemplo:
- →
- Nota: la mayoría de las personas usan calculadoras para encontrar la inversa de una matriz de 3 x 3 o más grande. Si quieres calcularlo a mano, consulta el final de esta sección.
-
2Toma el lado opuesto de los otros dos elementos, pero déjalos en posición. En otras palabras, multiplica los elementos de la esquina superior derecha y la esquina inferior izquierda por -1:
- →
-
3Obtén el recíproco del determinante. Encontraste el determinante de esta matriz en la sección anterior así que no tienes que calcularlo otra vez. Solo escribe el recíproco 1 / (determinante):
- En nuestro ejemplo, el determinante es 13. Su recíproco es .
-
4Multiplica la nueva matriz por el recíproco del determinante. Multiplica cada elemento de la nueva matriz por el recíproco que acabas de encontrar. La matriz que resulte es la inversa de la matriz de 2 x 2:
-
=
-
-
5Confirma que la inversa sea correcta. Para revisar tu trabajo, multiplica la inversa por la matriz original. Si la inversa es correcta, su producto siempre será la matriz identidad, . Si los cálculos dan resultado, pasa a la siguiente sección para terminar el problema.
- Para el problema de ejemplo, multiplica .
- Aquí puedes encontrar un curso de actualización sobre cómo multiplicar matrices.
- Nota: la multiplicación de matrices no es conmutativa, es decir, el orden de los factores importa. Sin embargo, al multiplicar una matriz por su inversa, ambas opciones darán como resultado la matriz identidad.[7]
-
6Revisa la inversión de matrices para las matrices de 3 x 3 o más grandes. A menos que estés aprendiendo este procedimiento por primera vez, ahorra tiempo usando una calculadora gráfica o software de matemáticas para las matrices más grandes. Si necesitas calcularlo a mano, este es un pequeño resumen de un método:[8] [9]
- Coloca la matriz identidad I a la derecha de tu matriz. Por ejemplo, [B] → [B | I ]. La matriz identidad tiene "1" elemento a lo largo de la diagonal principal y "0" elementos en todas las demás posiciones.
- Realiza operaciones de fila para reducir la matriz hasta que el lado izquierdo esté escalonado y luego continúa reduciendo hasta que el lado izquierdo sea la matriz identidad.
- Una vez que termines la operación, la matriz estará en la forma [I | B-1]. En otras palabras, el lado derecho será la inversa de la matriz original.
Parte 3
Parte 3 de 3:Multiplicar matrices para terminar el problema
-
1Escribe ambas ecuaciones posibles. En la matemática regular con cantidades escalares, la multiplicación es conmutativa: 2 x 6 = 6 x 2. Esto no aplica para las matrices, así que es posible que tengas que resolver dos problemas:
- [A] * [B]-1 es la solución de x para el problema x[B] = [A].
- [B]-1 * [A] es la solución de x para el problema [B]x = [A].
- Si esto es parte de una ecuación, asegúrate de realizar la misma operación en ambos lados. Si [A] = [C], entonces [B]-1[A] no es igual a [C][B]-1 porque [B]-1 está a la izquierda de [A] pero a la derecha de [C].[10]
-
2Encuentra las dimensiones de tu respuesta. Las dimensiones de la matriz final son las dimensiones externas de los dos factores. Tiene la misma cantidad de filas que la primera matriz y la misma cantidad de columnas que la segunda matriz.
- Regresando a nuestro ejemplo original, tanto como son matrices de 2 x 2, así que las dimensiones de la respuesta también serán de 2 x 2.
- Para usar un ejemplo más complicado, si [A] es una matriz de 4 x 3 y [B]-1 es una matriz de 3 x 3, las dimensiones de la matriz [A] * [B]-1 serán 4 x 3.
-
3Encuentra el valor del primer elemento. Consulta el artículo en el enlace para obtener instrucciones completas o refresca tu memoria con este resumen:
- Para encontrar la fila 1, columna 1 de [A][B]-1, encuentra el producto escalar de la fila 1 de [A] y la columna 2 de [B]-1. Es decir, para una matriz de 2 x 2, calcula .
- En nuestro ejemplo, , la fila 1 columna 1 de nuestra respuesta es:
.
-
4Repite el procedimiento del producto escalar para cada posición en la matriz. Por ejemplo, el elemento en la posición 2,1 es el producto escalar de la fila 2 de [A] y la columna 1 de [B]-1. Trata de terminar el ejemplo por tu cuenta. Debes obtener las siguientes respuestas:
- Si necesitas encontrar la otra solución, .
Consejos
- Puedes dividir una matriz entre un escalar dividiendo cada elemento de la matriz entre el escalar.
- Por ejemplo, la matriz dividida entre 2 = .
Advertencias
- Las calculadoras no siempre son 100 % fiables cuando se trata de cálculos con matrices. Por ejemplo, si tu calculadora te dice que un elemento es un número muy pequeño (2E-8, por ejemplo), lo más probable es que el valor sea cero.[11]
Referencias
- ↑ http://www.mathcentre.ac.uk/resources/Engineering%20maths%20first%20aid%20kit/latexsource%20and%20diagrams/5_6.pdf
- ↑ https://people.richland.edu/james/lecture/m116/matrices/operations.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/operations.html
- ↑ http://www.purplemath.com/modules/minors.htm
- ↑ http://www.mathwords.com/i/inverse_of_a_matrix.htm
- ↑ http://www.purplemath.com/modules/mtrxinvr2.htm
- ↑ http://www.mathwords.com/i/inverse_of_a_matrix.htm
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html




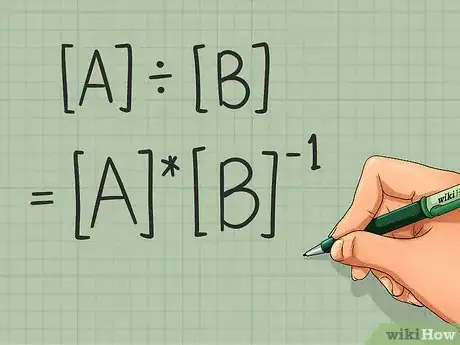



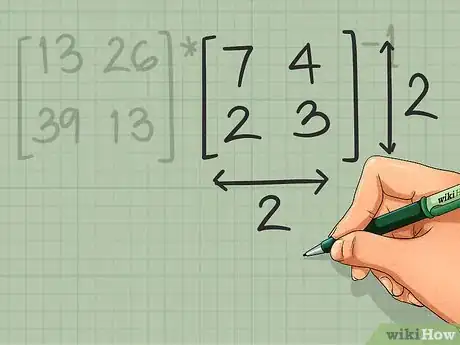

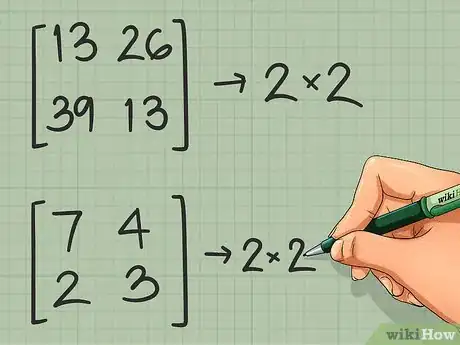
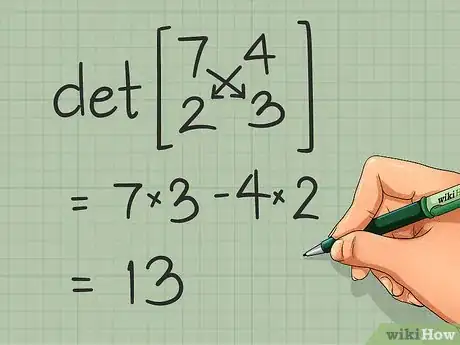

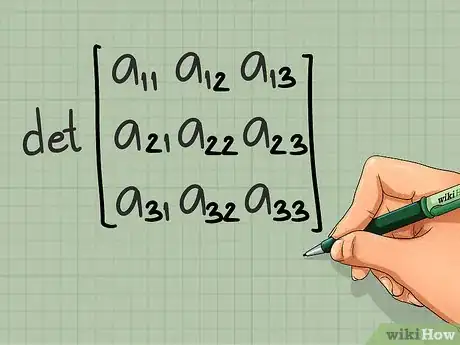
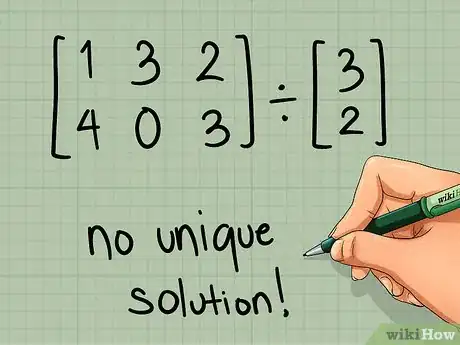
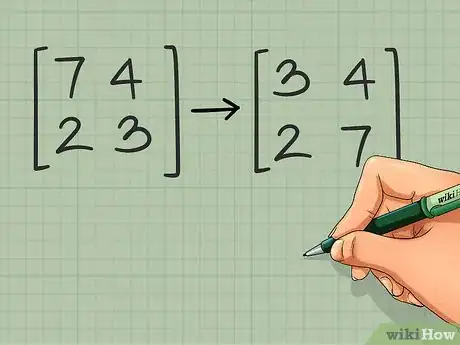

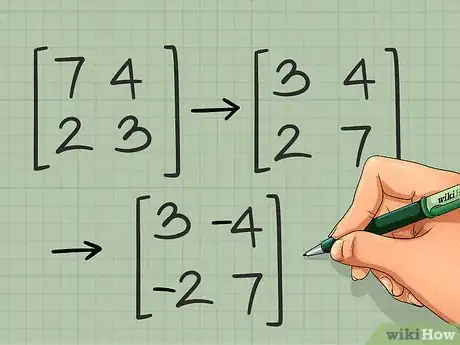

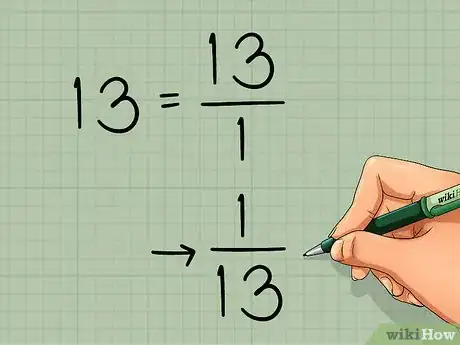

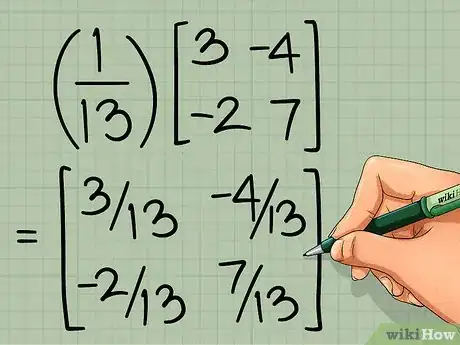


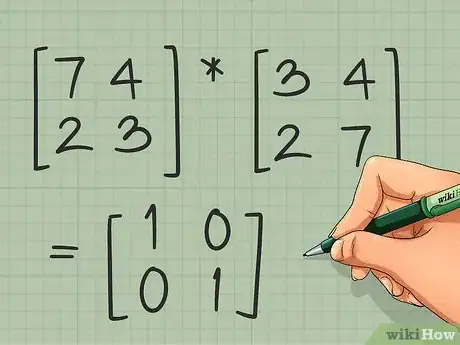


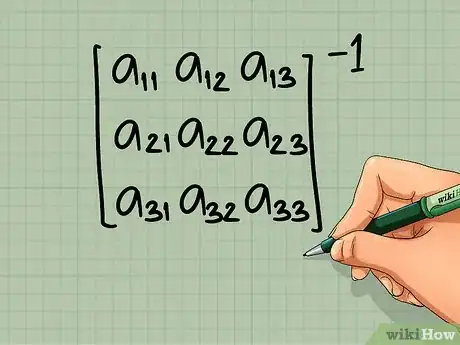
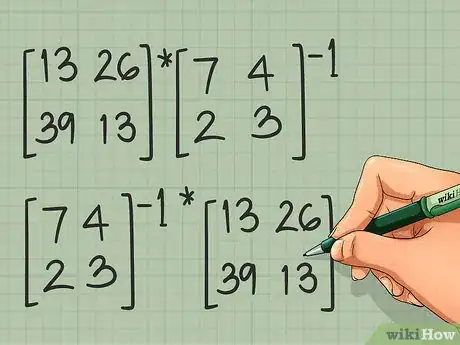
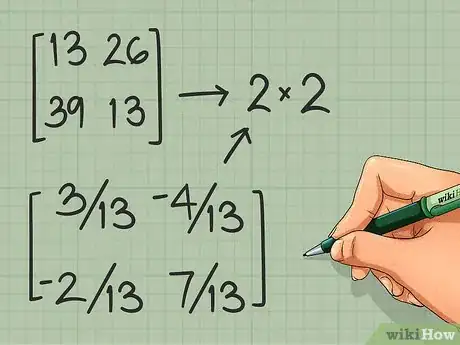

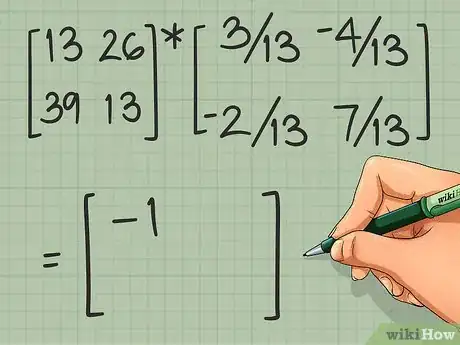





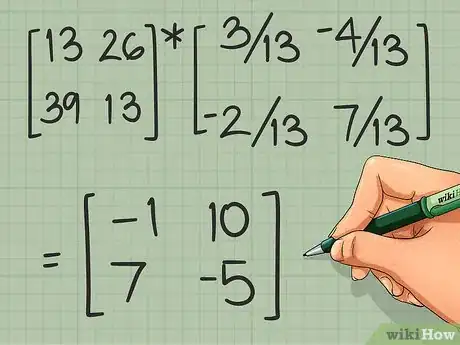























wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 106 533 veces.