Nuestro equipo de editores e investigadores capacitados han sido autores de este artículo y lo han validado por su precisión y amplitud.
wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad.
Este artículo ha sido visto 349 054 veces.
Los problemas con fracciones pueden parecer complicados al principio, pero se vuelven más fáciles con la práctica y el saber cómo resolverlos. Comienza por aprender la terminología y los fundamentos, luego practica sumar, restar, multiplicar y dividir fracciones. Una vez que entiendas lo que son las fracciones y cómo manipularlas, podrás resolver problemas con fracciones en poco tiempo.
Pasos
Método 1
Método 1 de 2:Practicar los fundamentos
-
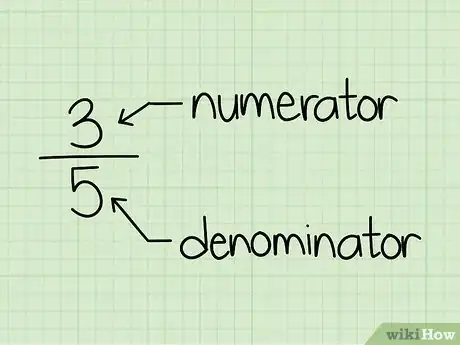
1Ten en cuenta que el numerador está en la parte superior y el denominador está en la parte inferior. Las fracciones se refieren a las partes de un todo, y el número superior en una fracción se llama el numerador. Este te indica con cuántas partes del todo vas a trabajar. Al número inferior en una fracción se le conoce como el denominador y te indica cuántas partes componen un todo.[1]
- Por ejemplo, en 3/5, 3 es el numerador, de modo que hay 3 partes y 5 es el denominador por lo que hay 5 partes en total. En 7/8, 7 es el numerador y 8, el denominador.
-
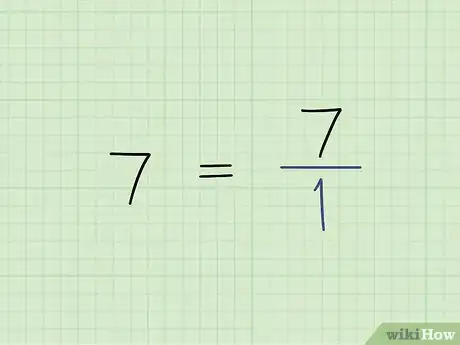
2Convierte un número entero en una fracción poniéndolo sobre 1. Si tienes un número entero y necesitas convertirlo a una fracción, puedes usar el número entero como numerador. Siempre usa 1 como el denominador ya que todo número indivisible tiene una sola parte.[2]
- Por ejemplo, si necesitas convertir 7 en una fracción, escríbela como 7/1.
-
3Reduce fracciones si necesitas simplificarlas. Comienza por encontrar el máximo factor común del numerador y el denominador. El máximo factor común es el número más grande entre el cual se puede dividir tanto el numerador como el denominador. Luego, simplemente divide el numerador y el denominador entre el máximo factor común para reducir la fracción.[3]
- Por ejemplo, si tienes la fracción 15/45, el máximo factor común es 15, ya que tanto 15 como 45 se pueden dividir entre 15. Divide 15 entre 15, lo cual es 1, de modo que ese es el nuevo numerador. Divide 45 entre 15, lo cual es 3, de modo que ese es el nuevo denominador. Esto significa que 15/45 se puede reducir a 1/3.
-
4Aprende a convertir números mixtos en fracciones impropias. Un número mixto tiene un número entero y una fracción. Para resolver ciertos problemas de fracciones más fácilmente, es posible que necesites convertir el número mixto en una fracción impropia (lo que significa que el número en la parte superior es mayor que el número en la parte inferior). Puedes hacerlo multiplicando el número entero por el denominador y añadiendo este número al numerador. Coloca el nuevo numerador sobre el denominador.[4]
- Digamos que tienes el número mixto 1 2/3. Comienza por multiplicar 3 por 1, lo cual es 3. Añade 3 al número 2, el cual es el numerador existente. El nuevo numerador es 5, por lo que la fracción mixta es 5/3.
Consejo: por lo general, necesitarás convertir los números mixtos en fracciones impropias si las vas a multiplicar o dividir.
-
5Averigua cómo convertir fracciones impropias en números mixtos. A veces, puedes tener el problema opuesto y la necesidad de convertir una fracción impropia en un número mixto. Comienza por averiguar cuántas veces el numerador puede entrar en el denominador usando la división. Esto se convertirá en el número entero. Halla el residuo multiplicando el número entero por el divisor (el número entre el cual vas a dividir) y restando el resultado del dividendo (el número que vas a dividir). Coloca el residuo sobre el denominador original.[5]
- Digamos que tienes la fracción impropia 17/4. Establece el problema como 17 ÷ 4. El número 4 cabe en el 17 un total de 4 veces, por lo que el número entero es 4. Luego, multiplica 4 por 4, que es igual a 16. Resta 16 de 17, que es igual a 1, de modo que es el residuo. Esto significa que 17/4 es lo mismo que 4 1/4.
Anuncio
Método 2
Método 2 de 2:Hacer cálculos con fracciones
-
1Suma fracciones con el mismo denominador mediante la combinación de los numeradores. Para sumar fracciones, deben tener el mismo denominador. Si lo hacen, simplemente suma los numeradores.[6]
- Por ejemplo, para resolver 5/9 + 1/9, solamente tienes que sumar 5 + 1, que es igual a 6. La respuesta, entonces, es 6/9 que se puede reducir a 2/3.
-
2Resta fracciones con el mismo denominador restando los numeradores. Si necesitas restar fracciones, deben tener el mismo denominador, al igual que si las fueses a sumar. Todo lo que tienes que hacer es restar el numerador más pequeño del numerador más grande para resolver el problema.[7]
- Por ejemplo, para resolver 6/8 - 2/8, todo lo que tienes que hacer es restar 2 de 6. La respuesta es 4/8, que se puede reducir a 1/2.
-
3Busca un múltiplo común para sumar o restar fracciones sin el mismo denominador. Si las fracciones no tienen el mismo denominador, necesitarás encontrar un múltiplo común de ambos denominadores y convertir cada fracción para que tengan el mismo denominador. Para ello, multiplica tanto el numerador como el denominador por el número que los convertirá al múltiplo común. Luego, suma o resta los numeradores para encontrar la respuesta.[8]
- Por ejemplo, si necesitas sumar 1/2 y 2/3, comienza por determinar un múltiplo común. En este caso, el múltiplo común es 6 ya que tanto 2 como 3 pueden convertirse en 6. Para convertir 1/2 en una fracción con un denominador de 6, multiplica el numerador y el denominador por 3: 1 x 3 = 3 y 2 x 3 = 6, por lo que la nueva fracción será 3/6. Para convertir 2/3 en una fracción con un denominador de 6, multiplica tanto el numerador como el denominador por 2: 2 x 2 = 4 y 3 x 2 = 6, así que la nueva fracción será 4/6. Ahora, puedes sumar los numeradores: 3/6 + 4/6 = 7/6. Puesto que esta es una fracción impropia, puedes convertirla en el número mixto 1 1/6.
- Por otro lado, digamos que vas a trabajar con el problema 7/10 - 1/5. El múltiplo común en este caso es 10, ya que 1/5 se puede convertir en una fracción con un denominador de 10 multiplicándolo por 2: 1 x 2 = 2 y 5 x 2 = 10, así que la nueva fracción será 2/10. No es necesario convertir la otra fracción en absoluto. Solamente resta 2 de 7, lo cual es 5. La respuesta es 5/10, la cual también se puede reducir a 1/2.
-
4Multiplica fracciones en línea recta. Afortunadamente, multiplicar fracciones es bastante fácil. Si las fracciones no se encuentran en los términos más bajos, redúcelas. Luego, todo lo que necesitas hacer es multiplicar el numerador por el numerador y el denominador por el denominador.[9]
- Por ejemplo, para multiplicar 2/3 y 7/8, busca el nuevo numerador multiplicando 2 por 7, lo cual es 14. Luego, multiplica 3 por 8, lo cual es 24. Por lo tanto, la respuesta es 14/24, la cual se puede reducir a 7/12 dividiendo el numerador y el denominador entre 2.
-
5Divide fracciones volteando la segunda fracción al revés y multiplicándola directamente. Para dividir fracciones, comienza por convertir la fracción que deseas dividir en un recíproco. Hazlo dándole vuelta hacia abajo para que el numerador se convierta en el denominador y el denominador se convierta en el numerador. Luego, multiplica ambos numeradores y ambos denominadores.[10]
- Por ejemplo, para resolver 1/2 1/6, voltea 1/6 al revés para que se convierta en 6/1. Entonces simplemente multiplica 1 x 6 para encontrar el numerador (el cual es 6) y 2 x 1 para encontrar el denominador (el cual es 2). Así, la respuesta es 6/2, lo cual es igual a 3.
Anuncio
Consejos
- Tómate el tiempo para leer cuidadosamente el problema al menos dos veces para estar seguro de que sabes lo que te pide que hagas.
- Consulta con tu profesor para averiguar si necesitas convertir fracciones impropias en números mixtos y/o reducir fracciones en sus términos más bajos para obtener calificaciones completas.
- Para obtener el recíproco de un número entero, basta con poner un 1 sobre él. Por ejemplo, 5 se convierte en 1/5.
- Las fracciones nunca pueden tener un denominador de cero. Un denominador de cero es indefinido, ya que la división entre cero es matemáticamente imposible.
Referencias
- ↑ https://medium.com/i-math/the-no-nonsense-straightforward-da76a4849ec
- ↑ https://medium.com/i-math/the-no-nonsense-straightforward-da76a4849ec
- ↑ http://www.math.com/school/subject1/lessons/S1U4L2GL.html
- ↑ https://sciencing.com/solve-math-problems-fractions-7964895.html
- ↑ https://sciencing.com/solve-math-problems-fractions-7964895.html
- ↑ https://www.bbc.co.uk/bitesize/articles/z9n4k7h
- ↑ https://www.bbc.co.uk/bitesize/articles/z9n4k7h
- ↑ https://www.bbc.co.uk/bitesize/articles/z9n4k7h
- ↑ http://www.math.com/school/subject1/lessons/S1U4L4GL.html




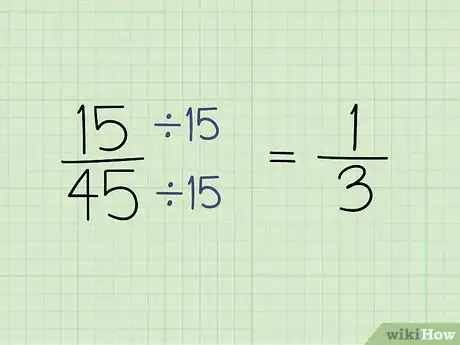
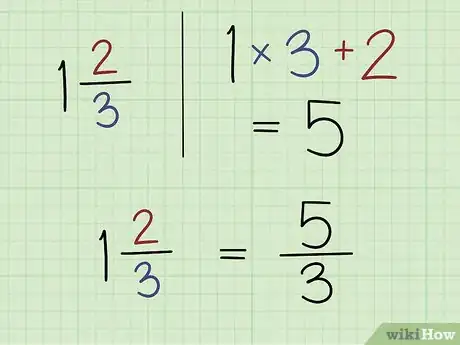

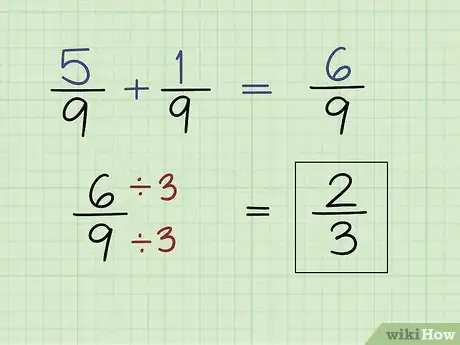

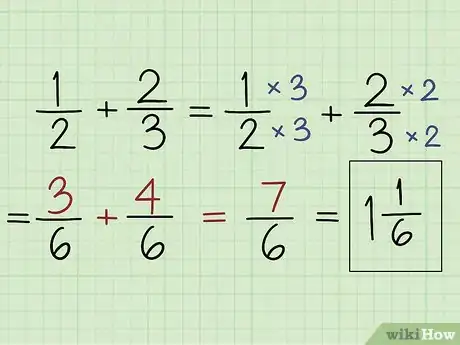

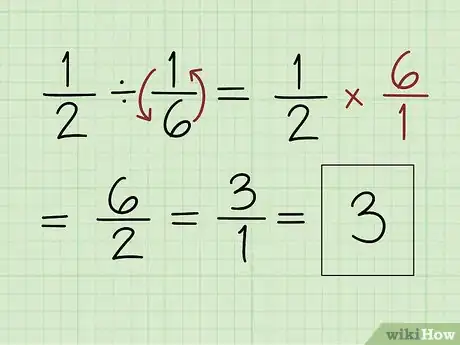



















wikiHow's Content Management Team revisa cuidadosamente el trabajo de nuestro personal editorial para asegurar que cada artículo cumpla con nuestros altos estándares de calidad. Este artículo ha sido visto 349 054 veces.