Comment calculer la surface d'un objet

Informations concernant l'auteur.e

Trouver la surface d'un objet géométrique est assez simple dans la mesure où l'on connait bien les formules de calcul des surfaces et qu'on sait les utiliser. Partant, quand vous passerez à des solides en trois dimensions, vous saurez également en calculer la surface totale extérieure. Voyons tout cela de plus près !

Partie 1

Partie 1 sur 2:
Calculer l'aire d'objets plans (en deux dimensions)

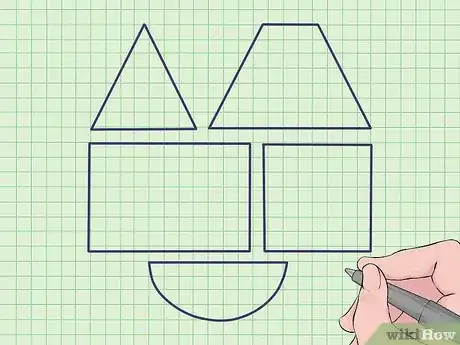
1
Identifiez en premier chacune des figures composant votre objet. Si votre problème ne concerne pas une figure géométrique simple, comme un cercle ou un trapèze, mais une forme plus complexe, il faut décomposer cette dernière en figures géométriques élémentaires. Vous devez identifier chacune de ces figures, c'est-à-dire trouver la forme et les dimensions de chacune.
- Dans l'illustration ci-dessus, la forme est composée des figures suivantes : un triangle, un trapèze, un rectangle, un carré et un demi-cercle (moitié de cercle).
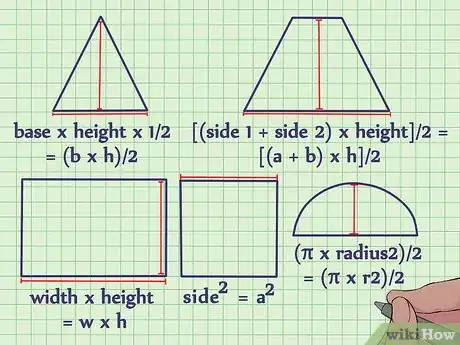
2
Inscrivez sur le papier les formules de calcul des aires de chacune de ces figures. Ces formules donnent la surface en fonction des mesures que vous avez. Voici les formules des figures les plus courantes en géométrie :
- aire d'un carré = côté² = a²
- aire d'un rectangle = largeur x hauteur = l x h
- aire d'un trapèze = [(côté1 + côté 2) x hauteur]/2 = [(a + b) x h]/2
- aire d'un triangle = base x hauteur x 1/2 = (b + h)/2
- aire d'un demi-cercle = (π x rayon²)/2 = (π x r²)/2
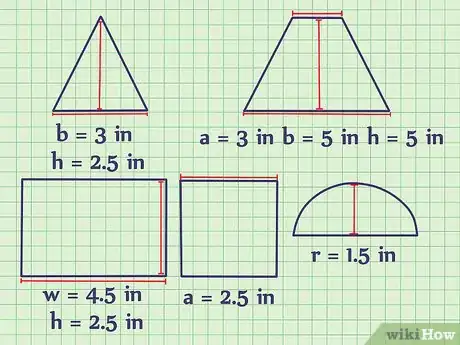
3
Inscrivez les dimensions de chacune des figures. Après avoir noté les formules de calcul, récupérez les dimensions de chacune des figures afin de les utiliser dans leurs formules respectives. Prenons donc les dimensions suivantes :
- pour le carré : a = 2,5 cm
- pour le rectangle : l = 4,5 cm, h = 2,5 cm
- pour le trapèze : a = 3 cm, b = 5 cm, h = 5 cm
- pour le triangle : b = 3 cm, h = 2,5 cm
- pour le demi-cercle : r = 1,5 cm
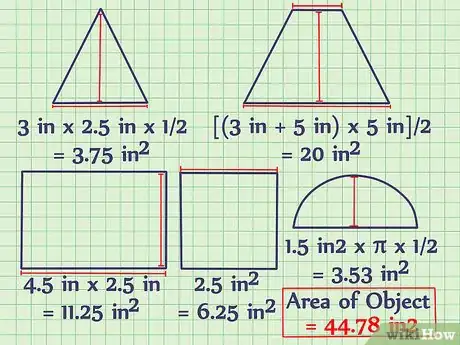
4
À partir des dimensions et des formules de calcul, trouvez les aires de chaque figure et additionnez-les. Vous le voyez sur l'illustration, l'objet de départ a été décomposé en figures élémentaires dont il faut, pour chacune, trouver l'aire en s'aidant des formules et des dimensions. Dans un deuxième temps, il suffira d'additionner toutes ces aires intermédiaires pour obtenir l'aire totale de l'objet. Les aires s'expriment en unités carrées (cm², m²…) L'aire totale de l'objet choisi est de 44,78 cm². Voici comment on obtient ce résultat :
- trouvez l'aire de chacune des figures :
  - aire du carré = (2,5 cm)² = 6,25 cm²
  - aire du rectangle = 4,5 cm x 2,5 cm = 11,25 cm²
  - aire du trapèze = [(3 cm + 5 cm) x 5 cm]/2 = 20 cm²
  - aire du triangle = 3 cm x 2,5 cm x 1/2 = 3,75 cm²
  - aire du demi-cercle = (1,5 cm)² x π x 1/2 = 3,53 cm²
- additionnez toutes ces aires :
  - aire de l'objet = aire du carré + aire du rectangle + aire du trapèze + aire du demi-cercle
  - aire de l'objet = 6,25 cm² + 11,25 cm² + 20 cm² + 3,75 cm² + 3,53 cm²
  - aire de l'objet = 44,78 cm²
Publicité

Partie 2

Partie 2 sur 2:
Calculer la surface totale des solides (en trois dimensions)

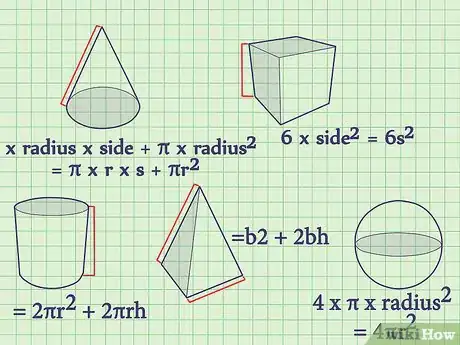
1
Inscrivez les formules qui vont vous servir à trouver la surface totale de chaque objet géométrique. La surface totale correspond à la totalité des surfaces des faces des solides, que ces faces soient planes ou courbes. Tout objet à trois dimensions a une surface totale, à l'extérieur ; le volume de l'objet est, quant à lui, tout l'espace occupé à l'intérieur des faces. Vous trouverez ci-dessous les formules de calcul des surfaces des principaux solides :
- surface totale d'un cube (de côté a) = 6 x côté² = 6a²
- surface totale d'un cône = (π x rayon x apothème) + (π x rayon²) = πra + πr²
- surface totale d'une sphère = 4 x π x rayon² = 4πr²
- surface totale d'un cylindre = 2 x π x rayon² + 2 x π x rayon x hauteur = 2πr² + 2πrh
- surface totale d'une pyramide de base carrée = côté de la base² + 2 x côté de la base x h = b² + 2bh
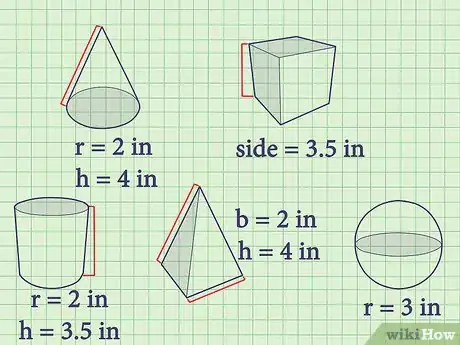
2
Inscrivez les dimensions de chaque figure. Les voici :
- pour le cube : côté = a = 3,5 cm,
- pour le cône : r = 2 cm, a = 4 cm,
- pour la sphère : r = 3 cm,
- pour le cylindre : r = 2 cm, h = 3,5 cm,
- pour la pyramide à base carrée : b = 2 cm, h = 4 cm.
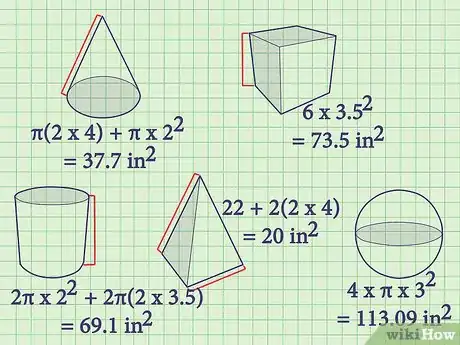
3
Calculez la surface de chaque solide. Vous avez maintenant toutes les dimensions utiles de chaque figure, il suffit de remplacer les lettres des formules par leurs valeurs respectives. Voici comment on procède :
- surface totale du cube = 6 x 3,5² = 73,5 cm²
- surface totale du cône = π (2 x 4) + π x 2² = 37,7 cm²
- surface totale de la sphère = 4 x π x 3² = 113,09 cm²
- surface totale du cylindre = 2π x 2² + 2π (2 x 3,5) = 69,1 cm²
- surface totale de la pyramide à base carrée = 2² + 2(2 x 4) = 20 cm²
Publicité

Conseils

Prenez vos mesures avec une règle ou à l'aide d'un pied à coulisse.

Avertissements

Ne confondez pas « aire » et « surface totale », qui sont assez proches, mais utilisées dans différents contextes. On appelle aire la surface d'objets plans et surface totale, la somme des surfaces de toutes les faces d'un solide.