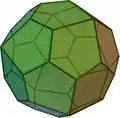
Poliedro
Un poliedro es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego antiguo πολύεδρον (polyedron), de la raíz πολύς (polys), «muchas» y de ἕδρα (hedra), «base», «asiento», «cara».


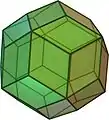
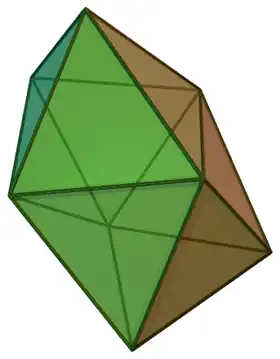


Los poliedros se conciben como cuerpos tridimensionales, pero hay semejantes topológicos del concepto en cualquier dimensión. Así, el punto o vértice es el semejante topológico del poliedro en cero dimensiones, una arista o segmento lo es en 1 dimensión, el polígono para 2 dimensiones; y el polícoro es el de cuatro dimensiones. Todas estas formas son conocidas como politopos, por lo que podemos definir un poliedro como un politopo tridimensional.

Definición
La definición más común de poliedro es la de una región acotada del espacio, delimitada solamente por polígonos planos.
Sin embargo, la definición puede cambiar dependiendo de si se interpreta un poliedro como un volumen, como los polígonos que lo delimitan, o como únicamente los segmentos que conforman el esqueleto del poliedro.
Esta y otras variaciones en la definición permiten la inclusión de otros términos, tales como las estelaciones, teselaciones, caras oblicuas, geometría no euclidiana, etc.
Denominación de los poliedros
El nombre dado a un poliedro depende de las propiedades del poliedro que sean relevantes en el contexto en que se esté mencionando.
Normalmente el nombre incluye:
- alguna cualidad acerca de las caras del poliedro, como su número (tetraedro (4), pentaedro (5), etc.); su forma (deltaedro (triangular), romboedro (rómbica), etc.); u otra cualidad
- propiedades que posea el poliedro (si es regular, toroidal, rómbico, etc.)
- transformaciones que han sido hechas en el poliedro (truncado, romo, estrellado, etc.)
Criterios de clasificación de los poliedros
Los poliedros pueden clasificarse según varios criterios:
- Los poliedros convexos contienen en su interior todos los segmentos que unen dos puntos también contenidos en el poliedro. En el caso de que dicho segmento se salga del cuerpo se dice que son poliedros cóncavos, como es el caso de los poliedros toroidales y los sólidos de Kepler-Poinsot.
- Los poliedros de caras regulares tienen solo polígonos regulares como caras.
- Los poliedros isoedrales o transitivos de caras poseen bajo las simetrías del poliedro una equivalencia entre cualquier par de caras.
- Los poliedros isotoxales o transitivos de aristas poseen bajo las simetrías del poliedro una equivalencia entre cualquier par de aristas.
- Los poliedros isogonales o transitivos de vértices poseen bajo las simetrías del poliedro una equivalencia entre cualquier par de vértices.
Estos en conjunto definen algunas de las principales familias de poliedros:
(Las propiedades en amarillo solo se encuentran en algunos (pero no todos) los poliedros de la familia.)
| Convexos | De caras regulares | Isoedrales | Isotoxales | Isogonales | Familia |
|---|---|---|---|---|---|
| Si | Si | No | No | No | Sólidos de Johnson |
| No nec. | Si | No | Si | Si | Poliedros cuasirregulares |
| No nec. | Si | No nec. | No nec. | Si | Poliedros uniformes |
| No nec. | No nec. | Si | No nec. | Si | Poliedros nobles |
| No nec. | Si | Si | Si | Si | Poliedros regulares |
| No | Si | Si | Si | Si | Sólidos de Kepler-Poinsot |
| Si | Si | Si | Si | Si | Sólidos platónicos |
Clasificación según el número de caras
El nombre que se le asigna a un poliedro según su número de caras se compone de un prefijo numeral más el sufijo ‑edro. La siguiente lista muestra varios ejemplos:
| Nombre | Número de caras |
|---|---|
| Henaedro o monoedro | 1 |
| Diedro | 2 |
| Triedro | 3 |
| Tetraedro | 4 |
| Pentaedro | 5 |
| Hexaedro | 6 |
| Heptaedro | 7 |
| Octaedro u octoedro | 8 |
| Eneaedro o nonaedro | 9 |
| Decaedro | 10 |
| Endecaedro o undecaedro | 11 |
| Dodecaedro | 12 |
| Tridecaedro | 13 |
| Tetradecaedro | 14 |
| Pentadecaedro | 15 |
| Hexadecaedro | 16 |
| Heptadecaedro | 17 |
| Octadecaedro u octodecaedro | 18 |
| Eneadecaedro o nonadecaedro | 19 |
| Icosaedro o isodecaedro | 20 |
| Triacontaedro o tricontaedro | 30 |
| Tetracontaedro | 40 |
| Pentacontaedro o pentecontaedro | 50 |
| Hectaedro o hecatontaedro | 100 |
| Chiliaedro | 1.000 |
| Miriaedro | 10.000 |
| Decamiriaedro | 100.000 |
| Hectamiriaedro o megaedro | 1.000.000 |
| Gigaedro | 1.000.000.000 |
| Quettaedro | 1030 |
| Googoledro | 10100 |
| Apeiroedro | infinitos |
| n-edro[lower-alpha 1] | n |
- n puede ser cualquier constante o variable escrita por su nombre o en dígitos.
Reglas de denominación
El prefijo numeral que forma parte de estos nombres se puede dividir según el dígito en el número de caras que es descrito por cada parte del prefijo.
Cada una de estas puede a su vez dividirse en dos partes: la primera (prefijo de dígito) indica el dígito al que se refiere (1, 2, 3, ..., hasta 9), y la segunda (prefijo de posición) indica la posición que lleva el dígito en el número de caras al que se refiere (decenas, centenas, etc.)
Además, se tiene que:
- Los 0s, la posición de los 1s y la del dígito en las unidades no se mencionan en el nombre
- Si el dígito en las decenas es un 1 o el número de caras termina en 12, las unidades se mencionan antes que las decenas
- El prefijo isodeca- puede reemplazarse por icosa-
La siguiente tabla muestra los distintos prefijos de dígito y de posición. Dependiendo de la posición del dígito correspondiente, los prefijos que se usan varían.
| Prefijo de dígito | Prefijo de posición | |||||
|---|---|---|---|---|---|---|
| Dígito | Posición del dígito correspondiente | Posición | Prefijo | |||
| Cualquiera | Unidades | Decenas | Centenas | |||
| 1 | en-, hena-, mono- o un-[lower-alpha 1] | 10 | conta- o deca-[lower-alpha 2] | |||
| 2 | di-[lower-alpha 3] | do-[lower-alpha 4] | iso- | dia-[lower-alpha 5] | 100 | cosi-, hecatonta- o hecta-[lower-alpha 6] |
| 3 | tri- | tria- | tria-[lower-alpha 7] | 1.000 | chilia- | |
| 4 | tetra- | 10.000 | miria- | |||
| 5 | penta- | pente- | 100.000 | decamiria- | ||
| 6 | hexa- | hexe- | 1.000.000 | hectamiria- o mega- | ||
| 7 | hepta- | 10.000.000 | decamega- | |||
| 8 | octa- | octo- | 100.000.000 | hectamega- | ||
| 9 | enea- o nona- | ...[lower-alpha 8] | ||||
- mono- solo se usa si el dígito en las decenas corresponde a 0, y en- o un- solo se usan si el dígito en las decenas es 1
- deca- se usa solo si el dígito en las decenas es 1 o 2, y conta- solo en caso contrario
- di- se usa solo si el dígito en las decenas es distinto 1 y el nombre no contiene el prefijo deca-
- do- se usa solo si el dígito en las decenas es 1
- dia- se usa en las centenas solo si el nombre contiene el prefijo cosi-
- hecatonta- se usa solo si el dígito correspondiente es 1, y cosi- solo en el caso contrario
- tria- se usa en las centenas solo si el nombre contiene el prefijo cosi-
- A partir del megaedro se utiliza el prefijo del SI correspondiente, y se añade antes el prefijo deca- o hecta- para especificar potencias de 10 intermedias.
Familias de poliedros
Poliedros regulares
Un poliedro regular es isoedral, isotoxal, isogonal, y todas sus caras son regulares. En total existen cinco poliedros regulares convexos, que corresponden a los sólidos platónicos; más 4 no convexos, que corresponden a los sólidos de Kepler-Poinsot y son estelaciones de sólidos platónicos; sumando 9 en total.
Sólidos platónicos
Los sólidos platónicos o sólidos de Platón son poliedros regulares y convexos. Solo existen cinco sólidos platónicos.
| Nombre | Imagen | Símbolo de Schläfli | Configuración de vértices |
|---|---|---|---|
| Tetraedro |  |
{3,3} | 3.3.3 |
| Cubo o hexaedro regular |  |
{4,3} | 4.4.4 |
| Octaedro |  |
{3,4} | 3.3.3.3 |
| Dodecaedro |  |
{5,3} | 5.5.5 |
| Icosaedro |  |
{3,5} | 3.3.3.3.3 |
Sólidos de Kepler-Poinsot
Los sólidos de Kepler-Poinsot o sólidos de Kepler son poliedros regulares y que, a diferencia de los sólidos platónicos, no son convexos. Solo hay cuatro de ellos y se obtienen como estelaciones del dodecaedro o del icosaedro.
| Nombre | Imagen | Símbolo de Schläfli | Configuración de vértices |
|---|---|---|---|
| Gran dodecaedro |  |
{5,5⁄2} | (55)/2 |
| Pequeño dodecaedro estrellado |  |
{5⁄2,5} | (5⁄2)5 |
| Gran icosaedro |  |
{3,5⁄2} | (35)/2 |
| Gran dodecaedro estrellado |  |
{5⁄2,3} | (5⁄2)3 |
Poliedros irregulares
Los poliedros irregulares son aquellos que tienen desigualdades entre sus caras, aristas y/o vértices.
Sólidos arquimedianos
Los sólidos arquimedianos o sólidos de Arquímedes son poliedros convexos y uniformes pero no transitivos de caras, y no incluyen a la familia infinita de los poliedros prismáticos. Fueron ampliamente estudiados por Arquímedes. Algunos se obtienen truncando los sólidos platónicos. Solo hay trece sólidos arquimedianos.
| Nombre | Imagen | Configuración de vértices |
|---|---|---|
| Tetraedro truncado | 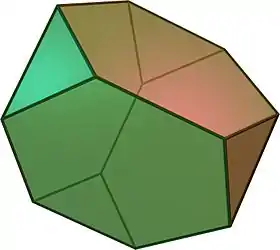 |
3.6.6 |
| Cuboctaedro | 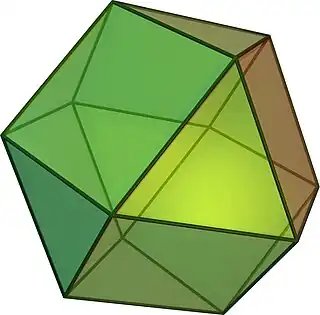 |
3.4.3.4 |
| Cubo truncado | 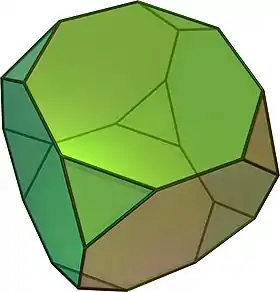 |
3.8.8 |
| Octaedro truncado | 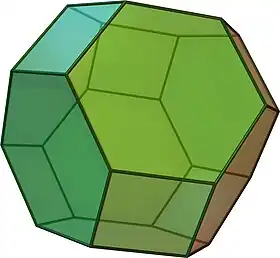 |
4.6.6 |
| Rombicuboctaedro |  |
3.4.4.4 |
| Cuboctaedro truncado | 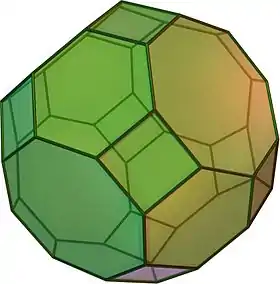 |
4.6.8 |
| Cubo romo | 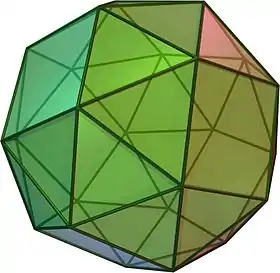 |
3.3.3.3.4 |
| Icosidodecaedro | 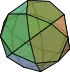 |
3.5.3.5 |
| Dodecaedro truncado |  |
3.10.10 |
| Icosaedro truncado |  |
5.6.6 |
| Rombicosidodecaedro |  |
3.4.5.4 |
| Icosidodecaedro truncado |  |
4.6.10 |
| Dodecaedro romo |  |
3.3.3.3.5 |
Prismas y antiprismas
El resto de poliedros convexos y uniformes consiste de prismas y antiprismas, los cuales en conjunto llevan el nombre de poliedros prismáticos. Las familias de los prismas y antiprismas son ambas infinitas.
Todos los prismas uniformes se construyen con dos caras paralelas llamadas bases, directrices o caras directrices, y una serie de cuadrados, tantos como lados tenga la cara directriz. Por ejemplo, el prisma cuyas caras directrices son triangulares se llama prisma triangular y se compone de dos triángulos y tres cuadrados.
Los antiprismas uniformes también contienen dos directrices, pero en este caso van unidas por triángulos, donde la base de cada triángulo va unida a una arista de una de las bases del antiprisma, y el vértice del mismo triángulo va unido a un vértice de la otra base.
Sólidos de Johnson
El resto de los poliedros convexos de caras regulares está conformado por los sólidos de Johnson. Este es un grupo extenso de poliedros convexos de caras regulares y no uniformes. Solo uno de estos, el Pseudorrombicuboctaedro, tiene la misma configuración en todos sus vértices (pero no es transitivo de vértices). Los sólidos de Johnson fueron clasificados y ampliamente estudiados por el matemático Norman Johnson. Solo hay 92 sólidos de Johnson.
Poliedros estrellados uniformes
Los poliedros estrellados uniformes son una familia de poliedros no convexos, isogonales y de caras regulares. Contiene dos familias infinitas, los prismas estrellados y los antiprismas estrellados, más otros 57 poliedros, 4 de los cuales son los sólidos de Kepler-Poinsot.
Sólidos de Catalan
Corresponden a los duales de los sólidos de Arquímedes (el dual es básicamente el reemplazo de las caras por vértices y viceversa, de manera que las uniones entre los vértices del dual coincidan con las uniones entre las caras del poliedro original). Por ejemplo, el dual del icosaedro (de 20 caras y 12 vértices) es el dodecaedro (de 12 caras y 20 vértices), y viceversa. Los sólidos de Catalan son isoedrales, pero no de caras regulares.
Deltaedros
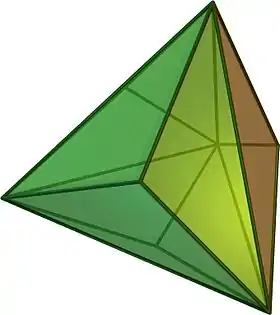
Se llama deltaedros a los cuerpos que solo están formados por triángulos equiláteros. Solo hay ocho deltaedros convexos. Tres de ellos pertenecen a los sólidos platónicos: el tetraedro, el octaedro y el icosaedro; y los otros cinco a los sólidos de Johnson: la bipirámide triangular, la bipirámide pentagonal, la bipirámide cuadrada giroelongada, el biesfenoide romo y el prisma triangular triaumentado.
| Nombre | Imagen |
|---|---|
| Tetraedro |  |
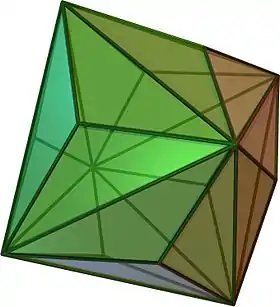
| Octaedro |  |
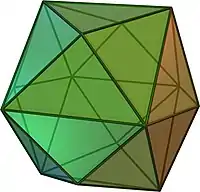
| Icosaedro | 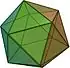 |
| Bipirámide triangular | 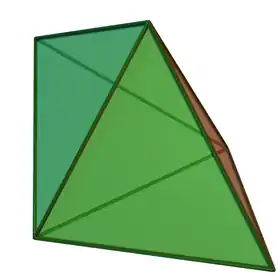 |
| Bipirámide pentagonal | 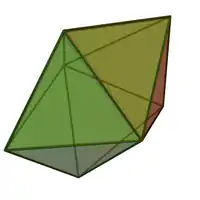 |
| Biesfenoide romo |  |
| Prisma triangular triaumentado | 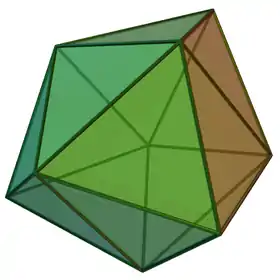 |
| Bipirámide cuadrada giroelongada | 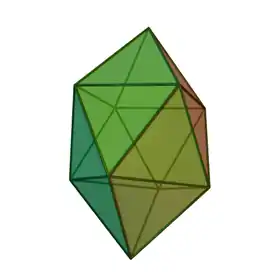 |
Trapezoedros
Los trapezoedros son los duales de los antiprismas.
Generalizaciones de poliedros
Apeiroedros
Se puede incluir como poliedros a aquellos que tienen una cantidad infinita de caras, llamados apeiroedros, entre los que se encuentran:
- Los teselados o teselaciones, las cuales son poliedros que llenan completamente el plano en el que se encuentran. Todos los ángulos diedros en una teselación son planos.
- Los poliedros oblicuos infinitos, los cuales tienen caras oblicuas o figuras de vértice oblicuas
Poliedros en el espacio no euclidiano
También se puede extender el concepto de poliedro hacia espacios no euclidianos:
- Un poliedro esférico es una teselación en la superficie de la esfera, donde las aristas corresponden a geodésicas.
- También es posible teselar un espacio hiperbólico.
Véase también
Bibliografía
- Quince Salas, Ricardo. Propiedades elementales de los poliedros regulares. Santander: [s.n.], 1974. 17 p. Comunicación presentada a las Reuniones sobre Geometría aplicada a la Arquitectura y a la Ingeniería Civil.
- Quince Salas, Ricardo. Áreas y volúmenes de cuerpos geométricos. Teoría y ejercicios. Santander: Escuela Superior de Ingenieros de Caminos, Canales y Puertos, [s.a.]. 202 p.
- Quince Salas, Ricardo. Áreas y volúmenes de cuerpos geométricos. Tomo 2: soluciones. Santander: Escuela Superior de Ingenieros de Caminos, Canales y Puertos, [s.a.]. 124 p.
Enlaces externos
 Wikimedia Commons alberga una galería multimedia sobre Poliedro.
Wikimedia Commons alberga una galería multimedia sobre Poliedro.
En español
Teoría general
- Weisstein, Eric W. «Polyhedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Polyhedra Pages (en inglés)
- Uniform Solution for Uniform Polyhedra by Dr. Zvi Har'El Archivado el 27 de noviembre de 2015 en Wayback Machine. (en inglés)
- Symmetry, Crystals and Polyhedra (en inglés)
Listas y bases de datos de poliedros
- Virtual Reality Polyhedra – La Enciclopedia de poliedros.
- Electronic Geometry Models – Contiene una revisada selección de poliedros con característica inusuales.
- Polyhedron Models – Poliedros virtuales. (en inglés)
- Modelos de papel de varios poliedros
- Polyhedra Viewer – Visor basado en web para ver las relaciones entre varios poliedros.
Software libre
- A Plethora of Polyhedra (en inglés) – Una colección interactiva y gratuita de poliedros en Java. Incluye redes, secciones planares, duales, truncamientos y estrellamientos de más de 300 poliedros.
- Hyperspace Star Polytope Slicer (en inglés) – Una applet en java para Explorer, incluye una variedad de opciones de visores 3d.
- openSCAD – Programa libre en multiplataforma para programadores. Los poliedros son unas de las formas que se pueden modelas con ellos. Hay un manual (OpenSCAD User Manual).
- OpenVolumeMesh (en inglés) – Una biblioteca en C++ en multiplataforma para manejar redes poliédricas. Desarrollado por el Aachen Computer Graphics Group, RWTH Aachen University.
- Polyhedronisme Archivado el 25 de abril de 2012 en Wayback Machine. – Una utilidad basada en web para generar modelos de poliedros que usa la Conway polyhedron notation. Los modelos se pueden exportar como imagen en 2D, o como 3D OBJ o ficheros VRML2. Los ficheros en 3D se pueden abrir con software CAD.
Recursos para hacer modelos físicos
- Paper Models of Polyhedra. Redes gratuitas de poliedros.
- Instrucciones sencillas para construir más de 30 poliedros de papel (en inglés)
- Polyhedra plaited with paper strips. Modelos de poliedros construidos sin usar pegamento.
- Adopt a Polyhedron (en inglés) - Vista interactiva, redes y datos para iompresoras 3D para todas los tipos de poliedros con hasta nueve vértices.