قائمة الثوابت الرياضية

• القيمة العددية للثابت: من المراجع العالمية كموقع ماثوورلد أو من موسوعة المتتاليات الصحيحة على الإنترنت والتي تعرف اختصارا باسم أويس ويكي (OEIS).
• لاتخ: الصيغة في تنسيق تخ.
• الصيغة الرياضية: المستخدمة في برنامج ولفرام ألفا.
• أويس: موسوعة على الإنترنت عن الأعداد الصحيحة.
• الكسر المستمر: وهو الكسر الذي يأخذ الصيغة التالية

${\displaystyle x=a_{0}+{\cfrac {1}{a_{1}+{\cfrac {1}{a_{2}+{\cfrac {1}{a_{3}+{\cfrac {1}{\ddots \,}}}}}}}}}$

• العام: عام اكتشاف الثابت.
• تنسيق الويب: القيمة بشكل مناسب على صفحات الإنترنت.
• النوع: نوع العدد.
  • ك: عدد كسري
  • غ.ك: عدد غير نسبي (عدد غير كسري)
  • ج : عدد جبري
  • م : عدد متسام
  • خ : عدد مركب

هذا الجدول يهتم بأهم الدوال والثوابت الرياضية على مر العصور:

القيمة العددية	الاسم	الرسومات	الرمز	لاتخ	الصيغة	النوع	أويس ويكي	الكسر المستمر	العام	تنسيق الويب
0.74048048969306104116	ثابت هيرميت تعبئة الكرات بنظام ثلاثي الأبعاد حدسية كيبلر [1]		${\displaystyle {\mu _{_{K}}}}$	${\displaystyle {\frac {\pi }{3{\sqrt {2}}}}{\color {white}......\color {black}}}$ أثبت توماس هيلز في عام 2014 أن حدثية كيبلر صحيحة.[2]	pi/(3 sqrt(2))		A093825	[0;1,2,1,5,1,4,2,2,1,1,2,2,2,6,1,1,1,5,2,1,1,1, ...]	1611	0.74048048969306104116931349834344894
22.45915771836104547342	pi^e [3]		${\displaystyle \pi ^{e}}$	${\displaystyle \pi ^{e}}$	pi^e		A059850	[22;2,5,1,1,1,1,1,3,2,1,1,3,9,15,25,1,1,5,...]		22.4591577183610454734271522045437350
2.80777024202851936522	ثابت فرانسين روبنسون [4]		${\displaystyle {F}}$	${\displaystyle \int _{0}^{\infty }{\frac {1}{\Gamma (x)}}\,dx.=e+\int _{0}^{\infty }{\frac {e^{-x}}{\pi ^{2}+\ln ^{2}x}}\,dx}$	N[int[0 to ∞] {1/Gamma(x)}]		A058655	[2;1,4,4,1,18,5,1,3,4,1,5,3,6,1,1,1,5,1,1,1...]	1978	2.80777024202851936522150118655777293
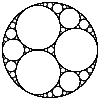
1.305686729 ≈ بواسطة توماس ودهار 1.305688 ≈ بواسطة ماكمولين	الهندسة الكسيرية لأبلونيوس البرغاوي [5]  · [6]		${\displaystyle \varepsilon }$				A052483	[0;3,2,3,16,8,10,3,1,1,2,1,3,1,2,13,1,1,4,1,5,...]	1994 1998	1.305686729 ≈ 1.305688 ≈
0.43828293672703211162 0.360592471871385485 i	الأس الانهائي للوحدة التخليلةi [7]		${\displaystyle {}^{\infty }{i}}$	${\displaystyle \lim _{n\to \infty }{}^{n}i=\lim _{n\to \infty }\underbrace {i^{i^{\cdot ^{\cdot ^{i}}}}} _{n}}$	i^i^i^i^i^i^...	خ	A077589  A077590	[0;2,3,1,1,4,2,2,1,10,2,1,3,1,8,2,1,2,1, ...] + [0;2,1,3,2,2,3,1,5,5,1,2,1,10,10,6,1,1...] i		0.43828293672703211162697516355126482 + 0.36059247187138548595294052690600 i
0.9288358271	مجموع مقلوب الأعداد الأولية التوأم		${\displaystyle B_{1}}$	${\displaystyle {\frac {1}{4}}+{\frac {1}{6}}+{\frac {1}{12}}+{\frac {1}{18}}+{\frac {1}{30}}+{\frac {1}{42}}+{\frac {1}{60}}+{\frac {1}{72}}+\cdots }$	1/4 + 1/6 + 1/12 + 1/18 + 1/30 + 1/42 + 1/60 + 1/72 + ...		A241560	[0; 1, 13, 19, 4, 2, 3, 1, 1]	2014	0.928835827131
0.63092975357145743709	مجموعة كانتور [8]		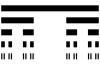${\displaystyle d_{f}(k)}$	${\displaystyle \lim _{\varepsilon \to 0}{\frac {\log N(\varepsilon )}{\log(1/\varepsilon )}}={\frac {\log 2}{\log 3}}}$	log(2)/log(3) N[3^x=2]	م	A102525	[0;1,1,1,2,2,3,1,5,2,23,2,2,1,1,55,1,4,3,1,1,...]		0.63092975357145743709952711434276085
0.31830988618379067153	مقلوب باي (π), سرينفاسا أينجار رامانجن[9]		${\displaystyle {\frac {1}{\pi }}}$	${\displaystyle {\frac {2{\sqrt {2}}}{9801}}\sum _{n=0}^{\infty }{\frac {(4n)!\,(1103+26390\;n)}{(n!)^{4}\,396^{4n}}}}$	2 sqrt(2)/9801 * Sum[n=0 to ∞] {((4n)!/n!^4) *(1103+ 26390n) / 396^(4n)}	م	A049541	[0;3,7,15,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,...]		0.31830988618379067153776752674502872
0.28878809508660242127	فلاجوليت وريتشموند [10]		${\displaystyle {Q}}$	${\displaystyle \prod _{n=1}^{\infty }\left(1-{\frac {1}{2^{n}}}\right)=\left(1{-}{\frac {1}{2^{1}}}\right)\left(1{-}{\frac {1}{2^{2}}}\right)\left(1{-}{\frac {1}{2^{3}}}\right)...}$	prod[n=1 to ∞] {1-1/2^n}		A048651	[0;3,2,6,4,1,2,1,9,2,1,2,3,2,3,5,1,2,1,1,6,1,...]	1992	0.28878809508660242127889972192923078
1.53960071783900203869	ثابت إليوت هرشل ليب للجليد (يستخدم في تحديد عدد المسارات الاويلرية) [11]		${\displaystyle {W}_{2D}}$	${\displaystyle \lim _{n\to \infty }(f(n))^{n^{-2}}=\left({\frac {4}{3}}\right)^{\frac {3}{2}}={\frac {8}{3{\sqrt {3}}}}}$	(4/3)^(3/2)	ج	A118273	[1;1,1,5,1,4,2,1,6,1,6,1,2,4,1,5,1,1,2,...]	1967	1.53960071783900203869106341467188655
0.20787957635076190854	${\displaystyle i^{i}}$ [12]		${\displaystyle i^{i}}$	${\displaystyle e^{-{\frac {\pi }{2}}}}$	e^(-π/2)	م	A049006	[0;4,1,4,3,1,1,1,1,1,1,1,1,7,1,20,1,3,6,10,...]	1746	0.20787957635076190854695561983497877
4.53236014182719380962	ثابت فان دير باو		${\displaystyle {\alpha }}$	${\displaystyle {\frac {\pi }{\ln(2)}}={\frac {\sum \limits _{n=0}^{\infty }{\frac {4(-1)^{n}}{2n+1}}}{\sum \limits _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}}}={\frac {{\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-\cdots }{{\frac {1}{1}}-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }}}$	π/ln(2)		A163973	[4;1,1,7,4,2,3,3,1,4,1,1,4,7,2,3,3,12,2,1,...]		4.53236014182719380962768294571666681
0.76159415595576488811	دالة زائدية للعدد 1 [13]		${\displaystyle {th}\,1}$	${\displaystyle -i\tan(i)={\frac {e-{\frac {1}{e}}}{e+{\frac {1}{e}}}}={\frac {e^{2}-1}{e^{2}+1}}}$	(e-1/e)/(e+1/e)	م	A073744	[0;1,3,5,7,9,11,13,15,17,19,21,23,25,27,...] = [0;2p+1], p∈ℕ		0.76159415595576488811945828260479359
0.59017029950804811302	ثابت تشيبيشيف [14] · [15]		${\displaystyle {\lambda _{Ch}}}$	${\displaystyle {\frac {\Gamma ({\tfrac {1}{4}})^{2}}{4\pi ^{3/2}}}={\frac {4({\tfrac {1}{4}}!)^{2}}{\pi ^{3/2}}}}$	(Gamma(1/4)^2) /(4 pi^(3/2))		A249205	[0;1,1,2,3,1,2,41,1,6,5,124,5,2,2,1,1,6,1,2,...]		0.59017029950804811302266897027924429
0.07077603931152880353 0.6840003894379-	MKB ثابت [16] · [17] · [18]		${\displaystyle M_{I}}$	${\displaystyle \lim _{n\rightarrow \infty }\int _{1}^{2n}(-1)^{x}~{\sqrt[{x}]{x}}~dx=\int _{1}^{2n}e^{i\pi x}~x^{1/x}~dx}$	lim_(2n->∞) int[1 to 2n] {exp(i*Pi*x)*x^(1/x) dx}	خ	A255727  A255728	[0;14,7,1,2,1,23,2,1,8,16,1,1,3,1,26,1,6,1,1, ...] - [0;1,2,6,13,41,112,1,25,1,1,1,1,3,13,2,1, ...] i	2009	0.07077603931152880353952802183028200 -0.68400038943793212918274445999266 i
1.259921049894873164767	الجذر التكعيبي للرقم 2		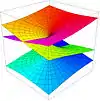${\displaystyle {\sqrt[{3}]{2}}}$	${\displaystyle {\sqrt[{3}]{2}}}$	2^(1/3)	ج	A002580	[1;3,1,5,1,1,4,1,1,8,1,14,1,10,2,1,4,12,2,3,...]		1.25992104989487316476721060727822835
1.09317045919549089396	ثابت سمراندش 1ª [19]		${\displaystyle {S_{1}}}$	${\displaystyle \sum _{n=2}^{\infty }{\frac {1}{\mu (n)!}}{\color {white}....\color {black}}}$ حيث μ(n) هو دالة كيمبنر			A048799	[1;10,1,2,1,2,1,13,3,1,6,1,2,11,4,6,2,15,1,1,...]		1.09317045919549089396820137014520832
0.62481053384382658687 + 1.30024 25902 20120 419 i	الكسر المستمر المعمم للوحدة التخليلية i		${\displaystyle {{F}_{CG}}_{(i)}}$	${\displaystyle \textstyle i{+}{\frac {i}{i+{\frac {i}{i+{\frac {i}{i+{\frac {i}{i+{\frac {i}{i+{\frac {i}{i+i{/...}}}}}}}}}}}}}={\sqrt {\frac {{\sqrt {17}}-1}{8}}}+i\left({\tfrac {1}{2}}{+}{\sqrt {\frac {2}{{\sqrt {17}}-1}}}\right)}$	i+i/(i+i/(i+i/(i+i/(i+i/( i+i/(i+i/(i+i/(i+i/(i+i/( i+i/(i+i/(i+i/(i+i/(i+i/( i+i/(i+i/(i+i/(i+i/(i+i/( ...)))))))))))))))))))))	ج	A156590  A156548	[i;1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,i,1,..] = [0;1,i]		0.62481053384382658687960444744285144 + 1.30024259022012041915890982074952 i
3.05940740534257614453	ثابت المضروب المزدوج		${\displaystyle {C_{_{n!!}}}}$	${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{n!!}}={\sqrt {e}}\left[{\frac {1}{\sqrt {2}}}+\gamma ({\tfrac {1}{2}},{\tfrac {1}{2}})\right]}$	Sum[n=0 to ∞]{1/n!!}		A143280	[3;16,1,4,1,66,10,1,1,1,1,2,5,1,2,1,1,1,1,1,2,...]		3.05940740534257614453947549923327861
5.97798681217834912266	ثابت ماديلونغ [20]		${\displaystyle {H}_{2}(2)}$	${\displaystyle \pi \ln(3){\sqrt {3}}}$	Pi Log[3]Sqrt[3]		A086055	[5;1,44,2,2,1,15,1,1,12,1,65,11,1,3,1,1,...]		5.97798681217834912266905331933922774
0.91893853320467274178	صيغة راب [21]		${\displaystyle {\zeta '(0)}}$	${\displaystyle \int \limits _{a}^{a+1}\log \Gamma (t)\,\mathrm {d} t={\tfrac {1}{2}}\log 2\pi +a\log a-a,\quad a\geq 0}$	integral_a^(a+1) {log(Gamma(x))+a-a log(a)} dx		A075700	[0;1,11,2,1,36,1,1,3,3,5,3,1,18,2,1,1,2,2,1,1,...]		0.91893853320467274178032973640561763
2.20741609916247796230	مسألة الأريكة المتحركة [22]		${\displaystyle {S_{_{H}}}}$	${\displaystyle {\frac {\pi }{2}}+{\frac {2}{\pi }}\,}$	pi/2 + 2/pi	م	A086118	[2;4,1,4,1,1,2,5,1,11,1,1,5,1,6,1,3,1,1,1,1,7,...]	1967	2.20741609916247796230685674512980889
1.17628081825991750654	عدد سالم،[23] تخيل ليمير		${\displaystyle {\sigma _{_{10}}}}$	${\displaystyle x^{10}+x^{9}-x^{7}-x^{6}-x^{5}-x^{4}-x^{3}+x+1}$	x^10+x^9-x^7-x^6 -x^5-x^4-x^3+x+1	ج	A073011	[1;5,1,2,17,1,7,2,1,1,2,4,7,2,2,1,1,15,1,1, ...	1983?	1.17628081825991750654407033847403505
0.37395581361920228805	ثابت إميل أرتين [24]		${\displaystyle {C}_{Artin}}$	${\displaystyle \prod _{n=1}^{\infty }\left(1-{\frac {1}{p_{n}(p_{n}-1)}}\right)\quad p_{n}\scriptstyle {\text{ = prime}}}$	Prod[n=1 to ∞] {1-1/(prime(n) (prime(n)-1))}		A005596	[0;2,1,2,14,1,1,2,3,5,1,3,1,5,1,1,2,3,5,46,...]	1999	0.37395581361920228805472805434641641
0.42215773311582662702	حجم رباعي الأسطح [25]		${\displaystyle {V_{_{R}}}}$	${\displaystyle {\frac {s^{3}}{12}}(3{\sqrt {2}}-49\,\pi +162\,\arctan {\sqrt {2}})}$	(3*Sqrt[2] - 49*Pi + 162*ArcTan[Sqrt[2]])/12		A102888	[0;2,2,1,2,2,7,4,4,287,1,6,1,2,1,8,5,1,1,1,1, ...]		0.42215773311582662702336591662385075
2.82641999706759157554	ثابت موراتا [26]		${\displaystyle {C_{m}}}$	${\displaystyle \prod _{n=1}^{\infty }{\underset {p_{n}:\,{prime}}{{\Big (}1+{\frac {1}{(p_{n}-1)^{2}}}{\Big )}}}}$	Prod[n=1 to ∞] {1+1/(prime(n) -1)^2}		A065485	[2;1,4,1,3,5,2,2,2,4,3,2,1,3,2,1,1,1,8,2,2,28,...]		2.82641999706759157554639174723695374
1.09864196439415648573	ثابت باريس		${\displaystyle C_{Pa}}$	${\displaystyle \prod _{n=2}^{\infty }{\frac {2\varphi }{\varphi +\varphi _{n}}}\;,\;\varphi {=}{Fi}}$  con  ${\displaystyle \varphi _{n}{=}{\sqrt {1{+}\varphi _{n{-}1}}}}$   y   ${\displaystyle \varphi _{1}{=}1}$			A105415	[1;10,7,3,1,3,1,5,1,4,2,7,1,2,3,22,1,2,5,2,1,...]		1.09864196439415648573466891734359621
2.39996322972865332223 بالراديان	الزاوية الذهبية [27]		${\displaystyle {b}}$	${\displaystyle (4-2\,\Phi )\,\pi =(3-{\sqrt {5}})\,\pi }$ = 137.5077640500378546 ...°	(4-2*Phi)*Pi	م	A131988	[2;2,1,1,1087,4,4,120,2,1,1,2,1,1,7,7,2,11,...]	1907	2.39996322972865332223155550663361385
1.64218843522212113687	ثابت ليبيسج [28]		${\displaystyle {L2}}$	${\displaystyle {\frac {1}{5}}+{\frac {\sqrt {25-2{\sqrt {5}}}}{\pi }}={\frac {1}{\pi }}\int _{0}^{\pi }{\frac {\left|\sin({\frac {5t}{2}})\right|}{\sin({\frac {t}{2}})}}\,dt}$	1/5 + sqrt(25 - 2*sqrt(5))/Pi	م	A226655	[1;1,1,1,3,1,6,1,5,2,2,3,1,2,7,1,3,5,2,2,1,1,...]	1910	1.64218843522212113687362798892294034
1.26408473530530111307	ثابت فارديt[29]		${\displaystyle {V_{c}}}$	${\displaystyle {\frac {\sqrt {3}}{\sqrt {2}}}\prod _{n\geq 1}\left(1+{1 \over (2e_{n}-1)^{2}}\right)^{\!1/2^{n+1}}}$			A076393	[1;3,1,3,1,2,5,54,7,1,2,1,2,3,15,1,2,1,1,2,1,...]	1991	1.26408473530530111307959958416466949
1.5065918849 ± 0.0000000028	مساحة مجموعة ماندلبرو [30]		${\displaystyle \gamma }$	${\displaystyle {\sqrt {6\pi -1}}-e=1.506591651\cdots }$			A098403	[1;1,1,37,2,2,1,10,1,1,2,2,4,1,1,1,1,5,4,...]	1912	1.50659177 +/- 0.00000008
1.6111149258083	ثابت المضروب الأسي		${\displaystyle {S_{Ef}}}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{(n{-}1)^{\cdot ^{\cdot ^{\cdot ^{2^{1}}}}}}}}=1{+}{\frac {1}{2^{1}}}{+}{\frac {1}{3^{2^{1}}}}+{\frac {1}{4^{3^{2^{1}}}}}+{\frac {1}{5^{4^{3^{2^{1}}}}}}{+}\cdots }$		م	A080219	[1; 1, 1, 1, 1, 2, 1, 808, 2, 1, 2, 1, 14,...]		1.61111492580837673611111111111111111
1.11786415118994497314	ثابت جوه شموتز [31]		${\displaystyle C_{GS}}$	${\displaystyle \int _{0}^{\infty }{\frac {\log(s+1)}{e^{s}-1}}\ ds=\!-\!\sum _{n=1}^{\infty }{\frac {e^{n}}{n}}Ei(-n)}$	Integrate{ log(s+1) /(E^s-1)}		A143300	[1;8,2,15,2,7,2,1,1,1,1,2,3,5,3,5,1,1,4,13,1,...]		1.11786415118994497314040996202656544
0.3181315052047641 ±1.337235701430689	النقط الثابتة على اللوغاريتم الأكبر[32] ·		${\displaystyle {-W(-1)}}$	${\displaystyle \lim _{n\rightarrow \infty }}$${\displaystyle f(x)=\underbrace {\log(\log(\log(\log(\cdots \log(\log(x))))))\,\!} \atop {\log _{s}{\text{ n times}}}}$ تختلف القيمة الابتدائية لx لتصبح ${\textstyle 0,1,e,e^{e},e^{e^{e}}}$, etc.	-W(-1)	خ	A059526  A059527	[-i;1 +2i,1+i,6-i,1+2i,-7+3i,2i,2,1-2i,-1+i,-, ...]		0.31813150520476413531265425158766451 -1.33723570143068940890116214319371 i
0.28016949902386913303	ثابت بيرنشتين [33]		${\displaystyle {\beta }}$	${\displaystyle \approx {\frac {1}{2{\sqrt {\pi }}}}}$	1/(2 sqrt(pi))	م	A073001	[0;3,1,1,3,9,6,3,1,3,14,34,2,1,1,60,2,2,1,1,...]	1913	0.28016949902386913303643649123067200
0.66016181584686957392	ثابت العددان الأوليان التوأمان [34]		${\displaystyle {C}_{2}}$	${\displaystyle \prod _{p=3}^{\infty }{\frac {p(p-2)}{(p-1)^{2}}}}$	prod[p=3 to ∞] {p(p-2)/(p-1)^2		A005597	[0;1,1,1,16,2,2,2,2,1,18,2,2,11,1,1,2,4,1,...]	1922	0.66016181584686957392781211001455577
1.22674201072035324441	ثابت معامل فيبوناتشي [35]		${\displaystyle F}$	${\displaystyle \prod _{n=1}^{\infty }\left(1-\left(-{\frac {1}{{\varphi }^{2}}}\right)^{n}\right)=\prod _{n=1}^{\infty }\left(1-\left({\frac {{\sqrt {5}}-3}{2}}\right)^{n}\right)}$	prod[n=1 to ∞] {1-((sqrt(5) -3)/2)^n}		A062073	[1;4,2,2,3,2,15,9,1,2,1,2,15,7,6,21,3,5,1,23,...]		1.22674201072035324441763023045536165
0.11494204485329620070	ثابت كيبلر-بووكمب [36]		${\displaystyle {\rho }}$	${\displaystyle \prod _{n=3}^{\infty }\cos \left({\frac {\pi }{n}}\right)=\cos \left({\frac {\pi }{3}}\right)\cos \left({\frac {\pi }{4}}\right)\cos \left({\frac {\pi }{5}}\right)...}$	prod[n=3 to ∞] {cos(pi/n)}		A085365	[0;8,1,2,2,1,272,2,1,41,6,1,3,1,1,26,4,1,1,...]		0.11494204485329620070104015746959874
1.78723165018296593301	ثابت كومورنيك-لوريتي [37]		${\displaystyle {q}}$	${\displaystyle 1=\!\sum _{n=1}^{\infty }{\frac {t_{k}}{q^{k}}}\qquad \scriptstyle {\text{Raiz real de}}\displaystyle \prod _{n=0}^{\infty }\!\left(\!1{-}{\frac {1}{q^{2^{n}}}}\!\right)\!{+}{\frac {q{-}2}{q{-}1}}=0}$	FindRoot[(prod[n=0 to ∞] {1-1/(x^2^n)}+(x-2) /(x-1))= 0, {x, 1.7}, WorkingPrecision->30]	م	A055060	[1;1,3,1,2,3,188,1,12,1,1,22,33,1,10,1,1,7,...]	1998	1.78723165018296593301327489033700839
3.30277563773199464655	القيمة البرونزية [38]		${\displaystyle {\sigma }_{\,Rr}}$	${\displaystyle {\frac {3+{\sqrt {13}}}{2}}=1+{\sqrt {3+{\sqrt {3+{\sqrt {3+{\sqrt {3+\cdots }}}}}}}}}$	(3+sqrt 13)/2	ج	A098316	[3;3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,...] = [3;3,...]		3.30277563773199464655961063373524797
0.82699334313268807426	تغطية القرص [39]		${\displaystyle {C_{5}}}$	${\displaystyle {\frac {1}{\sum \limits _{n=0}^{\infty }{\frac {1}{\binom {3n+2}{2}}}}}={\frac {3{\sqrt {3}}}{2\pi }}}$	3 Sqrt[3]/(2 Pi)	م	A086089	[0;1,4,1,3,1,1,4,1,2,2,1,1,7,1,4,4,2,1,1,1,1,...]	1939 1949	0.82699334313268807426698974746945416
2.66514414269022518865	ثابتة غيلفوند–شنايدر [40]		${\displaystyle G_{\,GS}}$	${\displaystyle 2^{\sqrt {2}}}$	2^sqrt{2}	م	A007507	[2;1,1,1,72,3,4,1,3,2,1,1,1,14,1,2,1,1,3,1,...]	1934	2.66514414269022518865029724987313985
3.27582291872181115978	ثابت ليفي [41]		${\displaystyle \gamma }$	${\displaystyle e^{\pi ^{2}/(12\ln 2)}}$	e^(\pi^2/(12 ln(2))		A086702	[3;3,1,1,1,2,29,1,130,1,12,3,8,2,4,1,3,55,...]	1936	3.27582291872181115978768188245384386
0.52382257138986440645	دالة تشي		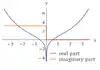${\displaystyle {\operatorname {Chi()} }}$	${\displaystyle \gamma +\int _{0}^{x}{\frac {\cosh t-1}{t}}\,dt}$ ${\displaystyle \scriptstyle \gamma \,{\text{= 0.5772156649...}}}$	Chi(x)		A133746	[0;1,1,9,1,172,1,7,1,11,1,1,2,1,8,1,1,1,1,1,...]		0.52382257138986440645095829438325566
1.1319882487943	ثابت فيسونث[42]		${\displaystyle {C}_{Vi}}$	${\displaystyle \lim _{n\to \infty }|a_{n}|^{\frac {1}{n}}}$      حيثan = عدد فيبوناتشي	lim_(n->∞) |a_n|^(1/n)	م	A078416	[1;7,1,1,2,1,3,2,1,2,1,8,1,5,1,1,1,9,1,...]	1997	1.1319882487943
1.23370055013616982735	ثابت فاراد [43]		${\displaystyle {\tfrac {3}{4}}\zeta (2)}$	${\displaystyle {\frac {\pi ^{2}}{8}}=\sum _{n=0}^{\infty }{\frac {1}{(2n-1)^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{5^{2}}}+{\frac {1}{7^{2}}}+\cdots }$	sum[n=1 to ∞] {1/((2n-1)^2)}	م	A111003	[1;4,3,1,1,2,2,5,1,1,1,1,2,1,2,1,10,4,3,1,1,...]	1902 a 1965	1.23370055013616982735431137498451889
2.50662827463100050241	الجذر التربيعي ل 2 باي		${\displaystyle {\sqrt {2\pi }}}$	${\displaystyle {\sqrt {2\pi }}=\lim _{n\to \infty }{\frac {n!\;e^{n}}{n^{n}{\sqrt {n}}}}{\color {white}....\color {black}}}$ تقريب ستيرلينغ	sqrt (2 pi)	م	A019727	[2;1,1,37,4,1,1,1,1,9,1,1,2,8,6,1,2,2,1,3,...]	1692 a 1770	2.50662827463100050241576528481104525
4.13273135412249293846	الجذر التربيعي لتاو* مشتقة الدالة الأسية للأساس e		${\displaystyle {\sqrt {\tau e}}}$	${\displaystyle {\sqrt {2\pi e}}}$	sqrt(2 pi e)		A019633	[4;7,1,1,6,1,5,1,1,1,8,3,1,2,2,15,2,1,1,2,4,...]		4.13273135412249293846939188429985264
0.97027011439203392574	ثابت لوتش [44]		${\displaystyle {{\text{£}}_{_{Lo}}}}$	${\displaystyle {\frac {6\ln 2\ln 10}{\pi ^{2}}}}$	6*ln(2)*ln(10)/Pi^2		A086819	[0;1,32,1,1,1,2,1,46,7,2,7,10,8,1,71,1,37,1,1,...]	1964	0.97027011439203392574025601921001083
0.98770039073605346013	المساحة المحيطة لمثلث رولو [45]		${\displaystyle {\mathcal {T}}_{R}}$	${\displaystyle a^{2}\cdot \left(2{\sqrt {3}}+{\frac {\pi }{6}}-3\right)}$    حيث a= طول ضلع المربع	2 sqrt(3)+pi/6-3	م	A066666	[0;1,80,3,3,2,1,1,1,4,2,2,1,1,1,8,1,2,10,1,2,...]	1914	0.98770039073605346013199991355832854
0.70444220099916559273	ثابت الإهمال 2 [46]		${\displaystyle {\mathcal {C}}_{2}}$	${\displaystyle {\underset {p_{n}:\,{prime}}{\prod _{n=1}^{\infty }\left(1-{\frac {1}{p_{n}(p_{n}+1)}}\right)}}}$	N[prod[n=1 to ∞] {1 - 1/(prime(n)* (prime(n)+1))}]		A065463	[0;1,2,2,1,1,1,1,4,2,1,1,3,703,2,1,1,1,3,5,1,...]		0.70444220099916559273660335032663721
1.84775906502257351225	معامل الربط [47][48]		${\displaystyle {\mu }}$	${\displaystyle {\sqrt {2+{\sqrt {2}}}}\;=\lim _{n\rightarrow \infty }c_{n}^{1/n}}$ دالة متعددة الحدود: ${\displaystyle \;x^{4}-4x^{2}+2=0}$	sqrt(2+sqrt(2))	ج	A179260	[1;1,5,1,1,3,6,1,3,3,10,10,1,1,1,5,2,3,1,1,3,...]		1.84775906502257351225636637879357657
0.30366300289873265859	ثابت جاووس-كوزمين-يرسينغ [49]		${\displaystyle {\lambda }_{2}}$	${\displaystyle \lim _{n\to \infty }{\frac {F_{n}(x)-\ln(1-x)}{(-\lambda )^{n}}}=\Psi (x),}$ حيث ${\displaystyle \Psi (x)}$ دالة تحليلية و ${\displaystyle \Psi (0)\!=\!\Psi (1)\!=\!0}$.			A038517	[0;3,3,2,2,3,13,1,174,1,1,1,2,2,2,1,1,1,2,2,1,...]	1973	0.30366300289873265859744812190155623
1.57079632679489661923	ثابت فارد K1 جداء واليس [50]		${\displaystyle {\frac {\pi }{2}}}$	${\displaystyle \prod _{n=1}^{\infty }\left({\frac {4n^{2}}{4n^{2}-1}}\right)={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdot {\frac {8}{7}}\cdot {\frac {8}{9}}\cdots }$	Prod[n=1 to ∞] {(4n^2)/(4n^2-1)}	م	A069196	[1;1,1,3,31,1,145,1,4,2,8,1,6,1,2,3,1,4,1,5,1...]	1655	1.57079632679489661923132169163975144
1.606695152415291763	ثابت إيردوس بروين[51][52]		${\displaystyle {E}_{\,B}}$	${\displaystyle \sum _{m=1}^{\infty }\sum _{n=1}^{\infty }{\frac {1}{2^{mn}}}=\sum _{n=1}^{\infty }{\frac {1}{2^{n}-1}}={\frac {1}{1}}\!+\!{\frac {1}{3}}\!+\!{\frac {1}{7}}\!+\!{\frac {1}{15}}\!+\!...}$	sum[n=1 to ∞] {1/(2^n-1)}	غ.ك	A065442	[1;1,1,1,1,5,2,1,2,29,4,1,2,2,2,2,6,1,7,1,...]	1949	1.60669515241529176378330152319092458
1.61803398874989484820	فاي، النسبة الذهبية [53]		${\displaystyle {\varphi }}$	${\displaystyle {\frac {1+{\sqrt {5}}}{2}}={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\cdots }}}}}}}}}$	(1+5^(1/2))/2	ج	A001622	[0;1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,...] = [0;1,...]	-300 ~	1.61803398874989484820458683436563811
1.64493406684822643647	دالة ريمان زيتا (2)		${\displaystyle {\zeta }(\,2)}$	${\displaystyle {\frac {\pi ^{2}}{6}}=\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+{\frac {1}{4^{2}}}+\cdots }$	Sum[n=1 to ∞] {1/n^2}	م	A013661	[1;1,1,1,4,2,4,7,1,4,2,3,4,10 1,2,1,1,1,15,...]	1826 to 1866	1.64493406684822643647241516664602519
1.73205080756887729352	الجذر التربيعي ل 3[54]		${\displaystyle {\sqrt {3}}}$	${\displaystyle {\sqrt[{3}]{3\,{\sqrt[{3}]{3\,{\sqrt[{3}]{3\,{\sqrt[{3}]{3\,{\sqrt[{3}]{3\,\cdots }}}}}}}}}}}$	(3(3(3(3(3(3(3) ^1/3)^1/3)^1/3) ^1/3)^1/3)^1/3) ^1/3 ...	ج	A002194	[1;1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,...] = [1;1,2,...]	-465 to -398	1.73205080756887729352744634150587237
1.75793275661800453270	عدد كاسنر		${\displaystyle {R}}$	${\displaystyle {\sqrt {1+{\sqrt {2+{\sqrt {3+{\sqrt {4+\cdots }}}}}}}}}$	Fold[Sqrt[#1+#2] &,0,Reverse [Range[20]]]		A072449	[1;1,3,7,1,1,1,2,3,1,4,1,1,2,1,2,20,1,2,2,...]	1878 a 1955	1.75793275661800453270881963821813852
2.29558714939263807403	ثابت القطع المكافئ العالمي [55]		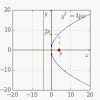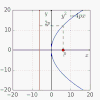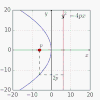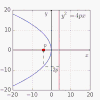${\displaystyle {P}_{\,2}}$	${\displaystyle \ln(1+{\sqrt {2}})+{\sqrt {2}}\;=\;\operatorname {arcsinh} (1)+{\sqrt {2}}}$	ln(1+sqrt 2)+sqrt 2	م	A103710	[2;3,2,1,1,1,1,3,3,1,1,4,2,3,2,7,1,6,1,8,7,2,1,...]		2.29558714939263807403429804918949038
1.78657645936592246345	ثابت سيلفرمان[56]		${\displaystyle {{\mathcal {S}}_{_{m}}}}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{\phi (n)\sigma _{1}(n)}}={\underset {p_{n}:\,{prime}}{\prod _{n=1}^{\infty }\left(1+\sum _{k=1}^{\infty }{\frac {1}{p_{n}^{2k}-p_{n}^{k-1}}}\right)}}}$ ø() = مؤشر أويلر، σ1() = دالة القواسم.	Sum[n=1 to ∞] {1/[EulerPhi(n) DivisorSigma(1,n)]}		A093827	[1;1,3,1,2,5,1,65,11,2,1,2,13,1,4,1,1,1,2,5,4,...]		1.78657645936592246345859047554131575
2.59807621135331594029	مساحة شكل سداسي منتظم مع جانب يساوي 1[57]		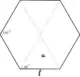${\displaystyle {\mathcal {A}}_{6}}$	${\displaystyle {\frac {3{\sqrt {3}}}{2}}}$	3 sqrt(3)/2	ج	A104956	[2;1,1,2,20,2,1,1,4,1,1,2,20,2,1,1,4,1,1,2,20,...] [2;1,1,2,20,2,1,1,4]		2.59807621135331594029116951225880855
0.66131704946962233528	ثابت فيلر تورنر [58]		${\displaystyle {{\mathcal {C}}_{_{FT}}}}$	${\displaystyle {\underset {p_{n}:\,{prime}}{{\frac {1}{2}}\prod _{n=1}^{\infty }\left(1-{\frac {2}{p_{n}^{2}}}\right){+}{\frac {1}{2}}}}={\frac {3}{\pi ^{2}}}\prod _{n=1}^{\infty }\left(1-{\frac {1}{p_{n}^{2}-1}}\right){+}{\frac {1}{2}}}$	[prod[n=1 to ∞] {1-2/prime(n)^2}] /2 + 1/2	م	A065493	[0;1,1,1,20,9,1,2,5,1,2,3,2,3,38,8,1,16,2,2,...]	1932	0.66131704946962233528976584627411853
1.46099848620631835815	ثابت باكستر [59]	Mapamundi Four-Coloring	${\displaystyle {\mathcal {C}}^{2}}$	${\displaystyle \prod _{n=1}^{\infty }{\frac {(3n-1)^{2}}{(3n-2)(3n)}}={\frac {3}{4\pi ^{2}}}\,\Gamma \left({\frac {1}{3}}\right)^{3}}$ Γ() = دالة غاما	3×Gamma(1/3) ^3/(4 pi^2)		A224273	[1;2,5,1,10,8,1,12,3,1,5,3,5,8,2,1,23,1,2,161,...]	1970	1.46099848620631835815887311784605969
1.92756197548292530426	ثابت تترنك		${\displaystyle {\mathcal {T}}}$	الجذور الموجبة للمعادلة التالية: ${\displaystyle \;\;x^{4}-x^{3}-x^{2}-x-1=0}$	Root[x+x^-4-2=0]	ج	A086088	[1;1,12,1,4,7,1,21,1,2,1,4,6,1,10,1,2,2,1,7,1,...]		1.92756197548292530426190586173662216
1.00743475688427937609	مكعب روبرت الرايني		${\displaystyle {f_{(3,4)}}}$	الجذور الموجبة للمعادلة التالية: ${\displaystyle \;\;4x^{4}{-}28x^{3}{-}7x^{2}{+}16x{+}16=0}$	Root[4*x^8-28*x^6 -7*x^4+16*x^2+16 =0]	ج	A243309	[1;134,1,1,73,3,1,5,2,1,6,3,11,4,1,5,5,1,1,48,...]		1.00743475688427937609825359523109914
1.70521114010536776428	ثابت نيفن [60]		${\displaystyle {C}}$	${\displaystyle 1+\sum _{n=2}^{\infty }\left(1-{\frac {1}{\zeta (n)}}\right)}$	1+ Sum[n=2 to ∞] {1-(1/Zeta(n))}		A033150	[1;1,2,2,1,1,4,1,1,3,4,4,8,4,1,1,2,1,1,11,1,...]	1969	1.70521114010536776428855145343450816
0.6045997880780726168	العلاقة بين مساحة مثلث متساوي الأضلاع والدائر بداخلة		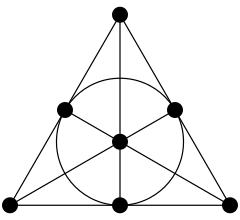${\displaystyle {\frac {\pi }{3{\sqrt {3}}}}}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n{2n \choose n}}}=1-{\frac {1}{2}}+{\frac {1}{4}}-{\frac {1}{5}}+{\frac {1}{7}}-{\frac {1}{8}}+\cdots }$ متسلسلة دركليه	Sum[1/(n Binomial[2 n, n]) , {n, 1, ∞}]	م	A073010	[0;1,1,1,1,8,10,2,2,3,3,1,9,2,5,4,1,27,27,6,6,...]		0.60459978807807261686469275254738524
1.15470053837925152901	ثابت هيرمت [61]		${\displaystyle \gamma _{_{2}}}$	${\displaystyle {\frac {2}{\sqrt {3}}}={\frac {1}{\cos \,({\frac {\pi }{6}})}}}$	2/sqrt(3)	ج	1+  A246724	[1;6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,...] [1;6,2]		1.15470053837925152901829756100391491
0.41245403364010759778	ثابت موروس [62]		${\displaystyle \tau }$	${\displaystyle \sum _{n=0}^{\infty }{\frac {t_{n}}{2^{n+1}}}}$    حيث ${\displaystyle \tau (x)=\sum _{n=0}^{\infty }(-1)^{t_{n}}\,x^{n}=\prod _{n=0}^{\infty }(1-x^{2^{n}})}$		م	A014571	[0;2,2,2,1,4,3,5,2,1,4,2,1,5,44,1,4,1,2,4,1,1,...]		0.41245403364010759778336136825845528
0.58057755820489240229	ثابت بيل [63]		${\displaystyle {{\mathcal {P}}_{_{Pell}}}}$	${\displaystyle 1-\prod _{n=0}^{\infty }\left(1-{\frac {1}{2^{2n+1}}}\right)}$	N[1-prod[n=0 to ∞] {1-1/(2^(2n+1)}]	م	A141848	[0;1,1,2,1,1,1,1,14,1,3,1,1,6,9,18,7,1,27,1,1,...]		0.58057755820489240229004389229702574
0.66274341934918158097	نهاية لابلاس [64]		${\displaystyle {\lambda }}$	${\displaystyle {\frac {x\;e^{\sqrt {x^{2}+1}}}{{\sqrt {x^{2}+1}}+1}}=1}$	(x e^sqrt(x^2+1)) /(sqrt(x^2+1)+1) = 1		A033259	[0;1,1,1,27,1,1,1,8,2,154,2,4,1,5,1,1,2,1601,...]	1782 ~	0.66274341934918158097474209710925290
0.17150049314153606586	ثابت هال مونتغمري [65]		${\displaystyle {{\delta }_{_{0}}}}$	${\displaystyle 1+{\frac {\pi ^{2}}{6}}+2\;\mathrm {Li} _{2}\left(-{\sqrt {e}}\;\right)\quad \mathrm {Li} _{2}\,\scriptstyle {\text{= Dilogarithm integral}}}$	1 + Pi^2/6 + 2*PolyLog[2, -Sqrt[E]]		A143301	[0;5,1,4,1,10,1,1,11,18,1,2,19,14,1,51,1,2,1,...]		0.17150049314153606586043997155521210
1.55138752454832039226	مثلث كالبي [66]		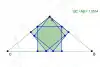${\displaystyle {C_{_{CR}}}}$	${\displaystyle {1 \over 3}+{(-23+3i{\sqrt {237}})^{\tfrac {1}{3}} \over 3\cdot 2^{\tfrac {2}{3}}}+{11 \over 3(2(-23+3i{\sqrt {237}}))^{\tfrac {1}{3}}}}$	FindRoot[ 2x^3-2x^2-3x+2 ==0, {x, 1.5}, WorkingPrecision->40]	ج	A046095	[1;1,1,4,2,1,2,1,5,2,1,3,1,1,390,1,1,2,11,6,2,...]	1946 ~	1.55138752454832039226195251026462381
1.22541670246517764512	غاما(3/4) [67]		${\displaystyle \Gamma ({\tfrac {3}{4}})}$	${\displaystyle \left(-1+{\frac {3}{4}}\right)!=\left(-{\frac {1}{4}}\right)!}$	(-1+3/4)!		A068465	[1;4,2,3,2,2,1,1,1,2,1,4,7,1,171,3,2,3,1,1,8,3,...]		1.22541670246517764512909830336289053
1.20205690315959428539	ثابت أبيري [68]		${\displaystyle \zeta (3)}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{3}}}={\frac {1}{1^{3}}}+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+{\frac {1}{5^{3}}}+\cdots =}$ ${\displaystyle {\frac {1}{2}}\sum _{n=1}^{\infty }{\frac {H_{n}}{n^{2}}}={\frac {1}{2}}\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }{\frac {1}{ij(i{+}j)}}=\!\!\int \limits _{0}^{1}\!\!\int \limits _{0}^{1}\!\!\int \limits _{0}^{1}{\frac {\mathrm {d} x\mathrm {d} y\mathrm {d} z}{1-xyz}}}$	Sum[n=1 to ∞] {1/n^3}	غ.ك	A010774	[1;4,1,18,1,1,1,4,1,9,9,2,1,1,1,2,7,1,1,7,11,...]	1979	1.20205690315959428539973816151144999
0.91596559417721901505	ثابت كاتالان[69][70][71]		${\displaystyle {C}}$	${\displaystyle \int _{0}^{1}\!\!\int _{0}^{1}\!\!{\frac {1}{1{+}x^{2}y^{2}}}\,dx\,dy=\!\sum _{n=0}^{\infty }\!{\frac {(-1)^{n}}{(2n{+}1)^{2}}}\!=\!{\frac {1}{1^{2}}}{-}{\frac {1}{3^{2}}}{+}{\cdots }}$	Sum[n=0 to ∞] {(-1)^n/(2n+1)^2}	م	A006752	[0;1,10,1,8,1,88,4,1,1,7,22,1,2,3,26,1,11,...]	1864	0.91596559417721901505460351493238411
0.78539816339744830961	بيتا(1) [72]		${\displaystyle {\beta }(1)}$	${\displaystyle {\frac {\pi }{4}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}={\frac {1}{1}}-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}-\cdots }$	Sum[n=0 to ∞] {(-1)^n/(2n+1)}	م	A003881	[0; 1,3,1,1,1,15,2,72,1,9,1,17,1,2,1,5,1,1,10,...]	1805 to 1859	0.78539816339744830961566084581987572
0.001317641154853178109	ثابت روجر هيث براون[73]		${\displaystyle {C_{_{HBM}}}}$	${\displaystyle {\underset {p_{n}:\,{prime}}{\prod _{n=1}^{\infty }\left(1-{\frac {1}{p_{n}}}\right)^{7}\left(1+{\frac {7p_{n}+1}{p_{n}^{2}}}\right)}}}$	N[prod[n=1 to ∞] {((1-1/prime(n))^7) *(1+(7*prime(n)+1) /(prime(n)^2))}]	م	A118228	[0;758,1,13,1,2,3,56,8,1,1,1,1,1,143,1,1,1,2,...]		0.00131764115485317810981735232251358
0.56755516330695782538	الوحدة النمطية للرفع الوحدة التخيليةi		${\displaystyle |{}^{\infty }{i}|}$	${\displaystyle \lim _{n\to \infty }\left|{}^{n}i\right|=\left|\lim _{n\to \infty }\underbrace {i^{i^{\cdot ^{\cdot ^{i}}}}} _{n}\right|}$	Mod(i^i^i^...)		A212479	[0;1,1,3,4,1,58,12,1,51,1,4,12,1,1,2,2,3,...]		0.56755516330695782538461314419245334
0.78343051071213440705	حلم الطالب الجامعي (1) ليوهان بيرنولي [74]		${\displaystyle {I}_{1}}$	${\displaystyle \int _{0}^{1}\!x^{x}\,dx=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{n}}}={\frac {1}{1^{1}}}-{\frac {1}{2^{2}}}+{\frac {1}{3^{3}}}-{\cdots }}$	Sum[n=1 to ∞] {-(-1)^n /n^n}		A083648	[0;1,3,1,1,1,1,1,1,2,4,7,2,1,2,1,1,1,2,1,14,...]	1697	0.78343051071213440705926438652697546
1.291285997062663540407	حلم الطالب الجامعي (2) ليوهان بيرنولي [75]		${\displaystyle {I}_{2}}$	${\displaystyle \int _{0}^{1}\!{\frac {1}{x^{x}}}\,dx=\sum _{n=1}^{\infty }{\frac {1}{n^{n}}}={\frac {1}{1^{1}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{4}}}+\cdots }$	Sum[n=1 to ∞] {1/(n^n)}		A073009	[1;3,2,3,4,3,1,2,1,1,6,7,2,5,3,1,2,1,8,1,2,4,...]	1697	1.29128599706266354040728259059560054
0.70523017179180096514	ثابت بريموريال [76]		${\displaystyle {P_{\#}}}$	${\displaystyle {\underset {p_{n}:\,{prime}}{\sum _{n=1}^{\infty }{\frac {1}{p_{n}\#}}={\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{30}}+{\frac {1}{210}}+...=\sum _{k=1}^{\infty }\prod _{n=1}^{k}{\frac {1}{p_{n}}}}}}$	Sum[k=1 to ∞] (prod[n=1 to k] {1/prime(n)})	غ.ك	A064648	[0;1,2,2,1,1,4,1,2,1,1,6,13,1,4,1,16,6,1,1,4,...]		0.70523017179180096514743168288824851
0.14758361765043327417	صيغة بيلي-بوروين-بلوف [77]		${\displaystyle {C}}$	${\displaystyle {\frac {1}{\pi }}\arctan {\frac {1}{2}}={\frac {1}{\pi }}\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2^{2n+1})(2n+1)}}}$ ${\displaystyle ={\frac {1}{\pi }}\left({\frac {1}{2}}-{\frac {1}{3\cdot 2^{3}}}+{\frac {1}{5\cdot 2^{5}}}-{\frac {1}{7\cdot 2^{7}}}+\cdots \right)}$	Arctan(1/2)/pi	م	A086203	[0;6,1,3,2,5,1,6,5,3,1,1,2,1,1,2,3,1,2,3,2,2,...]		0.14758361765043327417540107622474052
0.15915494309189533576	ثابت بلوف [78]		${\displaystyle {A}}$	${\displaystyle {\frac {1}{2\pi }}}$	1/(2 pi)	م	A086201	[0;6,3,1,1,7,2,146,3,6,1,1,2,7,5,5,1,4,1,2,42,...]		0.15915494309189533576888376337251436
0.29156090403081878013	ثابت ديمر ثنائي الأبعاد 2D, [79][80]		${\displaystyle {\frac {C}{\pi }}}$ C= ثابت كاتالان	${\displaystyle \int \limits _{-\pi }^{\pi }{\frac {\cosh ^{-1}\left({\frac {\sqrt {\cos(t)+3}}{\sqrt {2}}}\right)}{4\pi }}\,dt}$	N[int[-pi to pi] {arccosh(sqrt( cos(t)+3)/sqrt(2)) /(4*Pi)dt}]		A143233	[0;3,2,3,16,8,10,3,1,1,2,1,3,1,2,13,1,1,4,1,5,...]		0.29156090403081878013838445646839491
0.498015668118356042 0.15494982830181068512 i	المضروب (i)[81]		${\displaystyle {i}\,!}$	${\displaystyle \Gamma (1+i)=i\,\Gamma (i)=\int \limits _{0}^{\infty }{\frac {t^{i}}{e^{t}}}\mathrm {d} t}$	Integral_0^∞ t^i/e^t dt	خ	A212877  A212878	[0;6,2,4,1,8,1,46,2,2,3,5,1,10,7,5,1,7,2,...] - [0;2,125,2,18,1,2,1,1,19,1,1,1,2,3,34,...] i		0.49801566811835604271369111746219809 - 0.15494982830181068512495513048388 i
2.09455148154232659148	ثابت واليس		${\displaystyle W}$	${\displaystyle {\sqrt[{3}]{\frac {45-{\sqrt {1929}}}{18}}}+{\sqrt[{3}]{\frac {45+{\sqrt {1929}}}{18}}}}$	(((45-sqrt(1929)) /18))^(1/3)+ (((45+sqrt(1929)) /18))^(1/3)	ج	A007493	[2;10,1,1,2,1,3,1,1,12,3,5,1,1,2,1,6,1,11,4,...]	1616 to 1703	2.09455148154232659148238654057930296
0.723648402298200009408	ثابت سرناك		${\displaystyle {C_{sa}}}$	${\displaystyle \prod _{p>2}{\Big (}1-{\frac {p+2}{p^{3}}}{\Big )}}$	N[prod[k=2 to ∞] {1-(prime(k)+2) /(prime(k)^3)}]	م	A065476	[0;1,2,1,1,1,1,1,1,1,4,4,1,1,1,1,1,1,1,8,2,1,1,...]		0.72364840229820000940884914980912759
0.632120558828557678404	الثابت الزمني [82]		${\displaystyle {\tau }}$	${\displaystyle \lim _{n\to \infty }1-{\frac {!n}{n!}}=\lim _{n\to \infty }P(n)=\int _{0}^{1}e^{-x}dx=1{-}{\frac {1}{e}}=}$ ${\displaystyle \sum \limits _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n!}}={\frac {1}{1!}}{-}{\frac {1}{2!}}{+}{\frac {1}{3!}}{-}{\frac {1}{4!}}{+}{\frac {1}{5!}}{-}{\frac {1}{6!}}{+}\cdots }$	lim_(n->∞) (1- !n/n!) !n=subfactorial	م	A068996	[0;1,1,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,...] = [0;1,1,1,2n], n∈ℕ		0.63212055882855767840447622983853913
1.04633506677050318098	ثابت مينكوفسكي-سيجل [83]		${\displaystyle F_{1}}$	${\displaystyle \prod _{n=1}^{\infty }{\frac {n!}{{\sqrt {2\pi n}}\left({\frac {n}{e}}\right)^{n}{\sqrt[{12}]{1+{\tfrac {1}{n}}}}}}}$	N[prod[n=1 to ∞] n! /(sqrt(2*Pi*n) *(n/e)^n *(1+1/n) ^(1/12))]		A213080	[1;21,1,1,2,1,1,4,2,1,5,7,2,1,20,1,1,1134,3,..]	1867 1885 1935	1.04633506677050318098095065697776037
5.244115108584239620929	ثابت ليمنيسكيت [84]		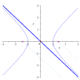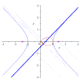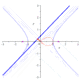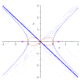${\displaystyle 2\varpi }$	${\displaystyle {\frac {[\Gamma ({\tfrac {1}{4}})]^{2}}{\sqrt {2\pi }}}=4\int _{0}^{1}{\frac {dx}{\sqrt {(1-x^{2})(2-x^{2})}}}}$	Gamma[ 1/4 ]^2 /Sqrt[ 2 Pi ]		A064853	[5;4,10,2,1,2,3,29,4,1,2,1,2,1,2,1,4,9,1,4,1,2,...]	1718	5.24411510858423962092967917978223883
0.661707182267176235155	ثابت روبين [85]		${\displaystyle \Delta (3)}$	${\displaystyle {\frac {4\!+\!17{\sqrt {2}}\!-6{\sqrt {3}}\!-7\pi }{105}}\!+\!{\frac {\ln(1\!+\!{\sqrt {2}})}{5}}\!+\!{\frac {2\ln(2\!+\!{\sqrt {3}})}{5}}}$	(4+17*2^(1/2)-6 *3^(1/2)+21*ln(1+ 2^(1/2))+42*ln(2+ 3^(1/2))-7*Pi)/105		A073012	[0;1,1,1,21,1,2,1,4,10,1,2,2,1,3,11,1,331,1,4,...]	1978	0.66170718226717623515583113324841358
1.30357726903429639125	ثابت كونواي [86]		${\displaystyle {\lambda }}$	${\displaystyle {\begin{smallmatrix}x^{71}\quad \ -x^{69}-2x^{68}-x^{67}+2x^{66}+2x^{65}+x^{64}-x^{63}-x^{62}-x^{61}-x^{60}\\-x^{59}+2x^{58}+5x^{57}+3x^{56}-2x^{55}-10x^{54}-3x^{53}-2x^{52}+6x^{51}+6x^{50}\\+x^{49}+9x^{48}-3x^{47}-7x^{46}-8x^{45}-8x^{44}+10x^{43}+6x^{42}+8x^{41}-5x^{40}\\-12x^{39}+7x^{38}-7x^{37}+7x^{36}+x^{35}-3x^{34}+10x^{33}+x^{32}-6x^{31}-2x^{30}\\-10x^{29}-3x^{28}+2x^{27}+9x^{26}-3x^{25}+14x^{24}-8x^{23}\quad \ -7x^{21}+9x^{20}\\+3x^{19}\!-4x^{18}\!-10x^{17}\!-7x^{16}\!+12x^{15}\!+7x^{14}\!+2x^{13}\!-12x^{12}\!-4x^{11}\!-2x^{10}\\+5x^{9}+x^{7}\quad \ -7x^{6}+7x^{5}-4x^{4}+12x^{3}-6x^{2}+3x-6\ =\ 0\quad \quad \quad \end{smallmatrix}}}$		ج	A014715	[1;3,3,2,2,54,5,2,1,16,1,30,1,1,1,2,2,1,14,1,...]	1987	1.30357726903429639125709911215255189
1.18656911041562545282	ثابت ليفي[87]		${\displaystyle {\beta }}$	${\displaystyle {\frac {\pi ^{2}}{12\,\ln 2}}}$	pi^2 /(12 ln 2)		A100199	[1;5,2,1,3,1,1,28,18,16,3,2,6,2,6,1,1,5,5,9,...]	1935	1.18656911041562545282172297594723712
0.83564884826472105333	مبرهنة باكر [88]		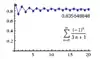${\displaystyle \beta _{3}}$	${\displaystyle \int _{0}^{1}{\frac {\mathrm {d} t}{1+t^{3}}}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{3n+1}}={\frac {1}{3}}\left(\ln 2+{\frac {\pi }{\sqrt {3}}}\right)}$	Sum[n=0 to ∞] {((-1)^(n))/(3n+1)}		A113476	[0;1,5,11,1,4,1,6,1,4,1,1,1,2,1,3,2,2,2,2,1,3,...]		0.83564884826472105333710345970011076
23.10344790942054161603	متتالية كيمبنر(0) [89]		${\displaystyle {K_{0}}}$	${\displaystyle 1{+}{\frac {1}{2}}{+}{\frac {1}{3}}{+}\cdots {+}{\frac {1}{9}}{+}{\frac {1}{11}}{+}\cdots {+}{\frac {1}{19}}{+}{\frac {1}{21}}{+}\cdots }$ ${\displaystyle {+}{\frac {1}{99}}{+}{\frac {1}{111}}{+}\cdots {+}{\frac {1}{119}}{+}{\frac {1}{121}}{+}\cdots }$	1+1/2+1/3+1/4+1/5 +1/6+1/7+1/8+1/9 +1/11+1/12+1/13 +1/14+1/15+...		A082839	[23;9,1,2,3244,1,1,5,1,2,2,8,3,1,1,6,1,84,1,...]		23.1034479094205416160340540433255981
0.989431273831146951741	ثابت ليبسج [90]		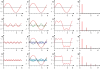${\displaystyle {C_{1}}}$	${\displaystyle \lim _{n\to \infty }\!\!\left(\!{L_{n}{-}{\frac {4}{\pi ^{2}}}\ln(2n{+}1)}\!\!\right)\!{=}{\frac {4}{\pi ^{2}}}\!\left({\sum _{k=1}^{\infty }\!{\frac {2\ln k}{4k^{2}{-}1}}}{-}{\frac {\Gamma '({\tfrac {1}{2}})}{\Gamma ({\tfrac {1}{2}})}}\!\!\right)}$	4/pi^2*[(2 Sum[k=1 to ∞] {ln(k)/(4*k^2-1)}) -poligamma(1/2)]		A243277	[0;1,93,1,1,1,1,1,1,1,7,1,12,2,15,1,2,7,2,1,5,...]		0.98943127383114695174164880901886671
0.19452804946532511361	المعامل الثاني لدي بو ريموند [91]		${\displaystyle {C_{2}}}$	${\displaystyle {\frac {e^{2}-7}{2}}=\int _{0}^{\infty }\left|{{\frac {d}{dt}}\left({\frac {\sin t}{t}}\right)^{n}}\right|\,dt-1}$	(e^2-7)/2	م	A062546	[0;5,7,9,11,13,15,17,19,21,23,25,27,29,31,...] = [0;2p+3], p∈ℕ		0.19452804946532511361521373028750390
0.78853056591150896106	ثابت لورث[92]		${\displaystyle C_{L}}$	${\displaystyle \sum _{n=2}^{\infty }{\frac {\ln \left({\frac {n}{n-1}}\right)}{n}}}$	Sum[n=2 to ∞] log(n/(n-1))/n		A085361	[0;1,3,1,2,1,2,4,1,127,1,2,2,1,3,8,1,1,2,1,16,...]		0.78853056591150896106027632216944432
1.187452351126501054595	ثابت غوياس α [93]		${\displaystyle F_{\alpha }}$	${\displaystyle x_{n+1}=\left(1+{\frac {1}{x_{n}}}\right)^{n}{\text{ for }}n=1,2,3,\ldots }$			A085848	[1;5,2,1,81,3,2,2,1,1,1,1,1,6,1,1,3,1,1,4,3,2,...]	2000	1.18745235112650105459548015839651935
2.293166287411861031508	ثابت غوياس β		${\displaystyle F_{\beta }}$	${\displaystyle x^{x+1}=(x+1)^{x}}$	x^(x+1) = (x+1)^x		A085846	[2;3,2,2,3,4,2,3,2,130,1,1,1,1,1,6,3,2,1,15,1,...]	2000	2.29316628741186103150802829125080586
0.82246703342411321823	ثابت نيسلون-رامانجن [94]		${\displaystyle {\frac {{\zeta }(2)}{2}}}$	${\displaystyle {\frac {\pi ^{2}}{12}}=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}}}={\frac {1}{1^{2}}}{-}{\frac {1}{2^{2}}}{+}{\frac {1}{3^{2}}}{-}{\frac {1}{4^{2}}}{+}{\frac {1}{5^{2}}}{-}\cdots }$	Sum[n=1 to ∞] {((-1)^(n+1))/n^2}	م	A072691	[0;1,4,1,1,1,2,1,1,1,1,3,2,2,4,1,1,1,1,1,1,4...]	1909	0.82246703342411321823620758332301259
0.69314718055994530941	اللوغارتم الطبيعي للرقم 2 [95]		${\displaystyle Ln(2)}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n2^{n}}}=\sum _{n=1}^{\infty }{\frac {({-}1)^{n+1}}{n}}={\frac {1}{1}}-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\cdots }}$	Sum[n=1 to ∞] {(-1)^(n+1)/n}	م	A002162	[0;1,2,3,1,6,3,1,1,2,1,1,1,1,3,10,1,1,1,2,1,1,...]	1550 to 1617	0.69314718055994530941723212145817657
0.47494937998792065033	ثابت ويرستراس [96]		${\displaystyle \sigma ({\tfrac {1}{2}})}$	${\displaystyle {\frac {e^{\frac {\pi }{8}}{\sqrt {\pi }}}{4\cdot 2^{3/4}{({\frac {1}{4}}!)^{2}}}}}$	(E^(Pi/8) Sqrt[Pi]) /(4 2^(3/4) (1/4)!^2)		A094692	[0;2,9,2,11,1,6,1,4,6,3,19,9,217,1,2,4,8,6...]	1872	0.47494937998792065033250463632798297
0.577215664901532860606	ثابت أويلر-ماسكيروني		${\displaystyle {\gamma }}$	${\displaystyle \sum _{n=1}^{\infty }\sum _{k=0}^{\infty }{\frac {(-1)^{k}}{2^{n}+k}}=\sum _{n=1}^{\infty }\left({\frac {1}{n}}-\ln \left(1+{\frac {1}{n}}\right)\right)}$ ${\displaystyle =\int _{0}^{1}-\ln \left(\ln {\frac {1}{x}}\right)\,dx=-\Gamma '(1)=-\Psi (1)}$	sum[n=1 to ∞] |sum[k=0 to ∞] {((-1)^k)/(2^n+k)}		A001620	[0;1,1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,1,...]	1735	0.57721566490153286060651209008240243
1.38135644451849779337	ثابت بيتا كينسر ماهلر لمتعددة الحدود[97]		${\displaystyle \beta }$	${\displaystyle e^{^{\textstyle {\frac {2}{\pi }}\displaystyle {\int _{0}^{\frac {\pi }{3}}}\textstyle {t\tan t\ dt}}}=e^{^{\displaystyle {\,\int _{\frac {-1}{3}}^{\frac {1}{3}}}\textstyle {\,\ln \lfloor 1+e^{2\pi it}}\rfloor dt}}}$	e^((PolyGamma(1,4/3) - PolyGamma(1,2/3) +9)/(4*sqrt(3)*Pi))		A242710	[1;2,1,1,1,1,1,4,1,139,2,1,3,5,16,2,1,1,7,2,1,...]	1963	1.38135644451849779337146695685062412
1.358456274182988435206	الدوامة الذهبية		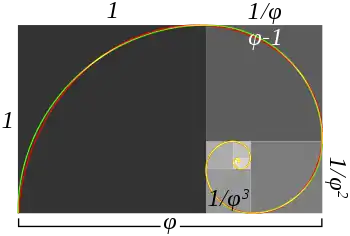${\displaystyle c}$	${\displaystyle \varphi ^{\frac {2}{\pi }}=\left({\frac {1+{\sqrt {5}}}{2}}\right)^{\frac {2}{\pi }}}$	GoldenRatio^(2/pi)		A212224	[1;2,1,3,1,3,10,8,1,1,8,1,15,6,1,3,1,1,2,3,1,1,...]		1.35845627418298843520618060050187945
0.57595996889294543964	ثابت ستيفين [98]		${\displaystyle C_{S}}$	${\displaystyle \prod _{n=1}^{\infty }\left(1-{\frac {p}{p^{3}-1}}\right)}$	Prod[n=1 to ∞] {1-hprime(n) /(hprime(n)^3-1)}	م	A065478	[0;1,1,2,1,3,1,3,1,2,1,77,2,1,1,10,2,1,1,1,7,...]		0.57595996889294543964316337549249669
0.73908513321516064165	عدد دوتي [99]		${\displaystyle d}$	${\displaystyle \lim _{x\to \infty }\cos ^{[x]}(c)=\lim _{x\to \infty }\underbrace {\cos(\cos(\cos(\cdots (\cos(c)))))} _{x}}$	cos(c)=c	م	A003957	[0;1,2,1,4,1,40,1,9,4,2,1,15,2,12,1,21,1,17,...]		0.73908513321516064165531208767387340
0.67823449191739197803	ثابت تانيجوتشي [100]		${\displaystyle C_{T}}$	خطأ رياضيات (خطأ في الصياغة): {\displaystyle \prod_{n = 1}^\infty \left(1 - \frac{3}{{p_n}^3}+\frac{2}{{p_n}^4}+�rac{1}{{p_n}^5}-�rac{1}{{p_n}^6} ight) } ${\displaystyle \scriptstyle p_{n}=\,ext{prime}}$	Prod[n=1 to ∞] {1 -3/ithprime(n)^3 +2/ithprime(n)^4 +1/ithprime(n)^5 -1/ithprime(n)^6}	م	A175639	[0;1,2,9,3,1,2,9,11,1,13,2,15,1,1,1,2,4,1,1,1,...]		0.67823449191739197803553827948289481
1.85407467730137191843	ثابت جاووس ليمنيسكيت[101]		${\displaystyle L{\text{/}}{\sqrt {2}}}$	${\displaystyle \int \limits _{0}^{\infty }{\frac {\mathrm {d} x}{\sqrt {1+x^{4}}}}={\frac {1}{4{\sqrt {\pi }}}}\,\Gamma \left({\frac {1}{4}}\right)^{2}={\frac {4\left({\frac {1}{4}}!\right)^{2}}{\sqrt {\pi }}}}$ ${\displaystyle \scriptstyle \Gamma (){\text{= Gamma function}}}$	pi^(3/2)/(2 Gamma(3/4)^2)		A093341	[1;1,5,1,5,1,3,1,6,2,1,4,16,3,112,2,1,1,18,1,...]		1.85407467730137191843385034719526005
1.75874362795118482469	ثابت الضرب اللانهائي [102]		${\displaystyle Pr_{1}}$	${\displaystyle \prod _{n=2}^{\infty }{\Big (}1+{\frac {1}{n}}{\Big )}^{\frac {1}{n}}}$	Prod[n=2 to inf] {(1+1/n)^(1/n)}		A242623	[1;1,3,6,1,8,1,4,3,1,4,1,1,1,6,5,2,40,1,387,2,...]	1977	1.75874362795118482469989684865589317
1.86002507922119030718	حلزون تيودوروس [103]		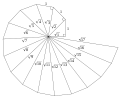${\displaystyle \partial }$	${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{{\sqrt {n^{3}}}+{\sqrt {n}}}}=\sum _{n=1}^{\infty }{\frac {1}{{\sqrt {n}}(n+1)}}}$	Sum[n=1 to ∞] {1/(n^(3/2) +n^(1/2))}		A226317	[1;1,6,6,1,15,11,5,1,1,1,1,5,3,3,3,2,1,1,2,19,...]	-460 to -399	1.86002507922119030718069591571714332
2.79128 78474 77920 00329	متداخلة جذرية S5		${\displaystyle S_{5}}$	${\displaystyle \displaystyle {\frac {{\sqrt {21}}+1}{2}}=\scriptstyle \,{\sqrt {5+{\sqrt {5+{\sqrt {5+{\sqrt {5+{\sqrt {5+\cdots }}}}}}}}}}\;}$ ${\displaystyle =1+\,\scriptstyle {\sqrt {5-{\sqrt {5-{\sqrt {5-{\sqrt {5-{\sqrt {5-\cdots }}}}}}}}}}\;}$	(sqrt(21)+1)/2	ج	A222134	[2;1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,1,3,...] [2;1,3]		2.79128784747792000329402359686400424
0.70710678118654752 br> +0.70710 67811 86547 524 i>	الجذر التربيعي للوحدة التخيليةi [104]		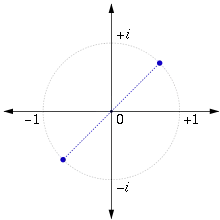${\displaystyle {\sqrt {i}}}$	${\displaystyle {\sqrt[{4}]{-1}}={\frac {1+i}{\sqrt {2}}}=e^{\frac {i\pi }{4}}=\cos \left({\frac {\pi }{4}}\right)+i\sin \left({\frac {\pi }{4}}\right)}$	(1+i)/(sqrt 2)	ج خ	A010503	[0;1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,..] = [0;1,2,...] [0;1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,..] i = [0;1,2,...] i		0.70710678118654752440084436210484903 + 0.70710678118654752440084436210484 i
0.809394020540639130717	ثابت اللادي – جرينستيد[105]		${\displaystyle {{\mathcal {A}}_{AG}}}$	${\displaystyle e^{-1+\sum \limits _{k=2}^{\infty }\sum \limits _{n=1}^{\infty }{\frac {1}{nk^{n+1}}}}=e^{-1-\sum \limits _{k=2}^{\infty }{\frac {1}{k}}\ln \left(1-{\frac {1}{k}}\right)}}$	e^{(sum[k=2 to ∞] |sum[n=1 to ∞] {1/(n k^(n+1))})-1}		A085291	[0;1,4,4,17,4,3,2,5,3,1,1,1,1,6,1,1,2,1,22,...]	1977	0.80939402054063913071793188059409131
2.58498175957925321706	ثابت شيربينسكي [106]		${\displaystyle {K}}$	${\displaystyle \pi \left(2\gamma +\ln {\frac {4\pi ^{3}}{\Gamma ({\tfrac {1}{4}})^{4}}}\right)=\pi (2\gamma +4\ln \Gamma ({\tfrac {3}{4}})-\ln \pi )}$ ${\displaystyle =\pi \left(2\ln 2+3\ln \pi +2\gamma -4\ln \Gamma ({\tfrac {1}{4}})\right)}$	-Pi Log[Pi]+2 Pi EulerGamma +4 Pi Log [Gamma[3/4]]		A062089	[2;1,1,2,2,3,1,3,1,9,2,8,4,1,13,3,1,15,18,1,...]	1907	2.58498175957925321706589358738317116
1.73245471460063347358	ثابت أويلر – ماتشيروني		${\displaystyle {\frac {1}{\gamma }}}$	${\displaystyle \left(\int _{0}^{1}-\log \left(\log {\frac {1}{x}}\right)\,dx\right)^{-1}=\sum _{n=1}^{\infty }(-1)^{n}(-1+\gamma )^{n}}$	1/Integrate_ {x=0 to 1} -log(log(1/x))		A098907	[1;1,2,1,2,1,4,3,13,5,1,1,8,1,2,4,1,1,40,1,11,...]		1.73245471460063347358302531586082968
1.435991124176917432355	ثابت يبيسج [107][108]		${\displaystyle {L_{1}}}$	${\displaystyle \prod _{\begin{smallmatrix}i=0\\j\neq i\end{smallmatrix}}^{n}{\frac {x-x_{i}}{x_{j}-x_{i}}}={\frac {1}{\pi }}\int _{0}^{\pi }{\frac {\lfloor \sin {\frac {3t}{2}}\rfloor }{\sin {\frac {t}{2}}}}\,dt={\frac {1}{3}}+{\frac {2{\sqrt {3}}}{\pi }}}$	1/3 + 2*sqrt(3)/pi	م	A226654	[1;2,3,2,2,6,1,1,1,1,4,1,7,1,1,1,2,1,3,1,2,1,1,...]	1902 ~	1.43599112417691743235598632995927221
3.24697960371746706105	الجذر الفضي [109]		${\displaystyle \varsigma }$	${\displaystyle 2+2\cos {\frac {2\pi }{7}}=\textstyle 2+{\frac {2+{\sqrt[{3}]{7+7{\sqrt[{3}]{7+7{\sqrt[{3}]{\,7+\cdots }}}}}}}{1+{\sqrt[{3}]{7+7{\sqrt[{3}]{7+7{\sqrt[{3}]{\,7+\cdots }}}}}}}}}$	2+2 cos(2Pi/7)	ج	A116425	[3;4,20,2,3,1,6,10,5,2,2,1,2,2,1,18,1,1,3,2,...]		3.24697960371746706105000976800847962
1.94359643682075920505	مؤشر أويلر [110][111]		${\displaystyle ET}$	${\displaystyle {\underset {p{\text{= primes}}}{\prod _{p}{\Big (}1+{\frac {1}{p(p-1)}}{\Big )}}}={\frac {\zeta (2)\zeta (3)}{\zeta (6)}}={\frac {315\zeta (3)}{2\pi ^{4}}}}$	zeta(2)*zeta(3) /zeta(6)		A082695	[1;1,16,1,2,1,2,3,1,1,3,2,1,8,1,1,1,1,1,1,1,32,...]	1750	1.94359643682075920505707036257476343
1.495348781221220541911	الجذر الرابع ل5 [112]		${\displaystyle {\sqrt[{4}]{5}}}$	${\displaystyle {\sqrt[{5}]{5\,{\sqrt[{5}]{5\,{\sqrt[{5}]{5\,{\sqrt[{5}]{5\,{\sqrt[{5}]{5\,\cdots }}}}}}}}}}}$	(5(5(5(5(5(5(5) ^1/5)^1/5)^1/5) ^1/5)^1/5)^1/5) ^1/5 ...	ج	A011003	[1;2,53,4,96,2,1,6,2,2,2,6,1,4,1,49,17,2,3,2,...]		1.49534878122122054191189899414091339
0.87228404106562797617	مساحة دائرة فورد [113]		${\displaystyle A_{CF}}$	${\displaystyle \sum _{q\geq 1}\sum _{(p,q)=1 \atop 1\leq p<q}\pi \left({\frac {1}{2q^{2}}}\right)^{2}{\underset {\zeta (){\text{= Riemann Zeta Function}}}{={\frac {\pi }{4}}{\frac {\zeta (3)}{\zeta (4)}}={\frac {45}{2}}{\frac {\zeta (3)}{\pi ^{3}}}}}}$	pi Zeta(3) /(4 Zeta(4))			[0;1,6,1,4,1,7,5,36,3,29,1,1,10,3,2,8,1,1,1,3,...]		0.87228404106562797617519753217122587
1.08232323371113819151	زيتا(4) [114]		${\displaystyle \zeta (4)}$	${\displaystyle {\frac {\pi ^{4}}{90}}=\sum _{n=1}^{\infty }{\frac {1}{n^{4}}}={\frac {1}{1^{4}}}+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+{\frac {1}{4^{4}}}+{\frac {1}{5^{4}}}+...}$	Sum[n=1 to ∞] {1/n^4}	م	A013662	[1;12,6,1,3,1,4,183,1,1,2,1,3,1,1,5,4,2,7,23,...]	?	1.08232323371113819151600369654116790
1.56155281280883027491	عدد مثلثي مربعي للرقم 2.[115]		${\displaystyle {R_{2}}}$	${\displaystyle {\frac {{\sqrt {17}}-1}{2}}=\,\scriptstyle {\sqrt {4+{\sqrt {4+{\sqrt {4+{\sqrt {4+{\sqrt {4+{\sqrt {4+\cdots }}}}}}}}}}}}\,\,-1}$ ${\displaystyle =\,\scriptstyle {\sqrt {4-{\sqrt {4-{\sqrt {4-{\sqrt {4-{\sqrt {4-{\sqrt {4-\cdots }}}}}}}}}}}}\textstyle }$	(sqrt(17)-1)/2	ج	A222133	[1;1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,1,3,1,...] [1;1,1,3]		1.56155281280883027491070492798703851
9.86960440108935861883	مربع باي		${\displaystyle {\pi }^{2}}$	${\displaystyle 6\,\zeta (2)=6\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {6}{1^{2}}}+{\frac {6}{2^{2}}}+{\frac {6}{3^{2}}}+{\frac {6}{4^{2}}}+\cdots }$	6 Sum[n=1 to ∞] {1/n^2}	م	A002388	[9;1,6,1,2,47,1,8,1,1,2,2,1,1,8,3,1,10,5,1,3,...]		9.86960440108935861883449099987615114
1.32471795724474602596	العدد البلاستيكي [116]		${\displaystyle {\rho }}$	${\displaystyle {\sqrt[{3}]{1+\!{\sqrt[{3}]{1+\!{\sqrt[{3}]{1+\cdots }}}}}}=\textstyle {\sqrt[{3}]{{\frac {1}{2}}+\!{\sqrt {\frac {23}{108}}}}}+\!{\sqrt[{3}]{{\frac {1}{2}}-\!{\sqrt {\frac {23}{108}}}}}}$	(1+(1+(1+(1+(1+(1) ^(1/3))^(1/3))^(1/3)) ^(1/3))^(1/3))^(1/3)	ج	A060006	[1;3,12,1,1,3,2,3,2,4,2,141,80,2,5,1,2,8,2,...]	1929	1.32471795724474602596090885447809734
2.37313822083125090564	ثابت ليفي2 [117]		${\displaystyle 2\,ln\,\gamma }$	${\displaystyle {\frac {\pi ^{2}}{6ln(2)}}}$	Pi^(2)/(6*ln(2))	م	A174606	[2;2,1,2,8,57,9,32,1,1,2,1,2,1,2,1,2,1,3,2,...]	1936	2.37313822083125090564344595189447424
0.85073618820186726036	متسلسلة طوي الورق [118][119]		${\displaystyle {P_{f}}}$	${\displaystyle \sum _{n=0}^{\infty }{\frac {8^{2^{n}}}{2^{2^{n+2}}-1}}=\sum _{n=0}^{\infty }{\cfrac {\tfrac {1}{2^{2^{n}}}}{1-{\tfrac {1}{2^{2^{n+2}}}}}}}$	N[Sum[n=0 to ∞] {8^2^n/(2^2^ (n+2)-1)},37]		A143347	[0;1,5,1,2,3,21,1,4,107,7,5,2,1,2,1,1,2,1,6,...]		0.85073618820186726036779776053206660
1.1563626843322697168533	ثابت تكرار المكعب [120][121]		${\displaystyle {\sigma _{3}}}$	${\displaystyle \prod _{n=1}^{\infty }n^{{3}^{-n}}={\sqrt[{3}]{1{\sqrt[{3}]{2{\sqrt[{3}]{3\cdots }}}}}}=1^{1/3}\;2^{1/9}\;3^{1/27}\cdots }$	prod[n=1 to ∞] {n ^(1/3)^n}		A123852	[1;6,2,1,1,8,13,1,3,2,2,6,2,1,2,1,1,1,10,33,...]		1.15636268433226971685337032288736935
1.261859507142914874199	البعد الكسري لمنحنى ندفة الثلج لكوخ [122]		${\displaystyle {C_{k}}}$	${\displaystyle {\frac {\log 4}{\log 3}}}$	log(4)/log(3)	م	A100831	[1;3,1,4,1,1,11,1,46,1,5,112,1,1,1,1,1,3,1,7,...]		1.26185950714291487419905422868552171
6.58088599101792097085	ثابت فورودا[123]		${\displaystyle 2^{\,e}}$	${\displaystyle 2^{e}}$	2^e			[6;1,1,2,1,1,2,3,1,14,11,4,3,1,1,7,5,5,2,7,...]		6.58088599101792097085154240388648649
0.26149 72128 47642 78375	ثابت ميرتنز-ميسيل [124]		${\displaystyle {M}}$	${\displaystyle \lim _{n\rightarrow \infty }\!\!\left(\sum _{p\leq n}{\frac {1}{p}}\!-\ln(\ln(n))\!\right)\!\!={\underset {\!\!\!\!\gamma$ :\,{\text{Euler constant}},\,\,p:\,{\text{prime}}}{\!\gamma \!+\!\!\sum _{p}\!\left(\!\ln \!\left(\!1\!-\!{\frac {1}{p}}\!\right)\!\!+\!{\frac {1}{p}}\!\right)}}}	gamma+ Sum[n=1 to ∞] {ln(1-1/prime(n)) +1/prime(n)}	م	A077761	[0;3,1,4,1,2,5,2,1,1,1,1,13,4,2,4,2,1,33,296,...]	1866 & 1873	0.26149721284764278375542683860869585
4.81047738096535165547	ثابت جون [125]		${\displaystyle \gamma }$	${\displaystyle {\sqrt[{i}]{i}}=i^{-i}=(i^{i})^{-1}=(((i)^{i})^{i})^{i}=e^{\frac {\pi }{2}}={\sqrt {\sum _{n=0}^{\infty }{\frac {\pi ^{n}}{n!}}}}}$	e^(π/2)	م	A042972	[4;1,4,3,1,1,1,1,1,1,1,1,7,1,20,1,3,6,10,3,2,...]		4.81047738096535165547303566670383313
- 0.5 ± 0.86602540378443 i	الجذر التكعيبي للرقم 1 [126]		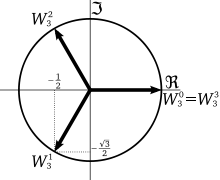${\displaystyle {\sqrt[{3}]{1}}}$	${\displaystyle {\begin{cases}\ \ 1\\-{\frac {1}{2}}+{\frac {\sqrt {3}}{2}}i\\-{\frac {1}{2}}-{\frac {\sqrt {3}}{2}}i.\end{cases}}}$	1, E^(2i pi/3), E^(-2i pi/3)	خ ج	A010527	- [0,5] ± [0;1,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,...] i - [0,5] ± [0; 1, 6, 2] i		- 0.5 ± 0.8660254037844386467637231707529 i
0.110001000000000000000001	عدد ليوفيل نص صغير[127]		${\displaystyle {\text{£}}_{Li}}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{10^{n!}}}={\frac {1}{10^{1!}}}+{\frac {1}{10^{2!}}}+{\frac {1}{10^{3!}}}+{\frac {1}{10^{4!}}}+\cdots }$	Sum[n=1 to ∞] {10^(-n!)}	م	A012245	[1;9,1,999,10,9999999999999,1,9,999,1,9]		0.11000100000000000000000100...
0.06598803584531253707	النهاية الصغرى لرفع الأساس e بالأس e.[128]		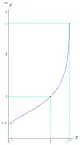${\displaystyle {e}^{-e}}$	${\displaystyle \left({\frac {1}{e}}\right)^{e}}$	1/(e^e)		A073230	[0;15,6,2,13,1,3,6,2,1,1,5,1,1,1,9,4,1,1,1,...]		0.06598803584531253707679018759684642
1.83928675521416113255	ثابت تريبوناكسي[129]		${\displaystyle {\phi _{}}_{3}}$	${\displaystyle \textstyle {\frac {1+{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}}{3}}=\scriptstyle \,1+\left({\sqrt[{3}]{{\tfrac {1}{2}}+{\sqrt[{3}]{{\tfrac {1}{2}}+{\sqrt[{3}]{{\tfrac {1}{2}}+...}}}}}}\right)^{-1}}$	(1/3)*(1+(19+3 *sqrt(33))^(1/3) +(19-3 *sqrt(33))^(1/3))	ج	A058265	[1;1,5,4,2,305,1,8,2,1,4,6,14,3,1,13,5,1,7,...]		1.83928675521416113255185256465328660
0.366512920581664327012	متوسط توزيع جامبل [130]		${\displaystyle {ll_{2}}}$	${\displaystyle -\ln(\ln(2))}$	-ln(ln(2))		A074785	[0;2,1,2,1,2,6,1,6,6,2,2,2,1,12,1,8,1,1,3,1,...]		0.36651292058166432701243915823266947
36.46215960720791177099	باي مرفوع بالأس باي [131]		${\displaystyle \pi ^{\pi }}$	${\displaystyle \pi ^{\pi }}$	pi^pi		A073233	[36;2,6,9,2,1,2,5,1,1,6,2,1,291,1,38,50,1,2,...]		36.4621596072079117709908260226921236
0.53964549119041318711	ثابت إيواتشيميسكو[132]		${\displaystyle 2+\zeta ({\tfrac {1}{2}})}$	${\displaystyle {2{-}(1{+}{\sqrt {2}})\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{\sqrt {n}}}}=\gamma +\sum _{n=1}^{\infty }{\frac {(-1)^{2n}\;\gamma _{n}}{2^{n}n!}}}$	γ + N[ sum[n=1 to ∞] {((-1)^(2n) gamma_n) /(2^n n!)}]		2-  A059750	[0;1,1,5,1,4,6,1,1,2,6,1,1,2,1,1,1,37,3,2,1,...]		0.53964549119041318711050084748470198
15.1542622414792641897	مجموعة الهروب [133]		${\displaystyle e^{e}}$	${\displaystyle \sum _{n=0}^{\infty }{\frac {e^{n}}{n!}}=\lim _{n\to \infty }\left({\frac {1+n}{n}}\right)^{n^{-n}(1+n)^{1+n}}}$	Sum[n=0 to ∞] {(e^n)/n!}		A073226	[15;6,2,13,1,3,6,2,1,1,5,1,1,1,9,4,1,1,1,6,7,...]		15.1542622414792641897604302726299119
0.64624543989481330426	ثابت جرمين-ماصر [134]		${\displaystyle {C}}$	${\displaystyle \gamma {\beta }(1)\!+\!{\beta }'(1)\!=\pi \!\left(-\!\ln \Gamma ({\tfrac {1}{4}})+{\tfrac {3}{4}}\pi +{\tfrac {1}{2}}\ln 2+{\tfrac {1}{2}}\gamma \right)}$ ${\displaystyle =\pi \!\left(-\!\ln({\tfrac {1}{4}}!)+{\tfrac {3}{4}}\ln \pi -{\tfrac {3}{2}}\ln 2+{\tfrac {1}{2}}\,\gamma \right)}$ ${\displaystyle \scriptstyle \gamma ={\text{Euler–Mascheroni constant}}=0.5772156649\ldots }$ ${\displaystyle \scriptstyle \beta ()={\text{Beta function}},\quad \scriptstyle \Gamma ()={\text{Gamma function}}}$	Pi/4*(2*Gamma + 2*Log[2] + 3*Log[Pi]- 4 Log[Gamma[1/4]])		A086057	[0;1,1,1,4,1,3,2,3,9,1,33,1,4,3,3,5,3,1,3,4,...]		0.64624543989481330426647339684579279
1.11072073453959156175	النسبة بين مربع محاط بدائرة [135]		${\displaystyle {\frac {\pi }{2{\sqrt {2}}}}}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {({-}1)^{\lfloor {\frac {n-1}{2}}\rfloor }}{2n+1}}={\frac {1}{1}}+{\frac {1}{3}}-{\frac {1}{5}}-{\frac {1}{7}}+{\frac {1}{9}}+{\frac {1}{11}}-{\cdots }}$	sum[n=1 to ∞] {(-1)^(floor( (n-1)/2)) /(2n-1)}	م	A093954	[1;9,31,1,1,17,2,3,3,2,3,1,1,2,2,1,4,9,1,3,...]		1.11072073453959156175397024751517342
1.45607494858268967139	ثابت باكهاوس [136]		${\displaystyle {B}}$	${\displaystyle \lim _{k\to \infty }\left|{\frac {q_{k+1}}{q_{k}}}\right\vert \quad \scriptstyle {\text{where:}}\displaystyle \;\;Q(x)={\frac {1}{P(x)}}=\!\sum _{k=1}^{\infty }q_{k}x^{k}}$ ${\displaystyle P(x)=\sum _{k=1}^{\infty }{\underset {p_{k}{\text{ prime}}}{p_{k}x^{k}}}=1+2x+3x^{2}+5x^{3}+\cdots }$	1/( FindRoot[0 == 1 + Sum[x^n Prime[n], {n, 10000}], {x, {1}})		A072508	[1;2,5,5,4,1,1,18,1,1,1,1,1,2,13,3,1,2,4,16,...]	1995	1.45607494858268967139959535111654355
1.85193705198246617036	ثابت غيبس [137]		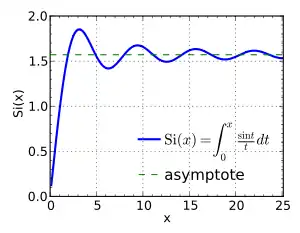${\displaystyle {Si(\pi )}}$ تكامل الجيب	${\displaystyle \int _{0}^{\pi }{\frac {\sin t}{t}}\,dt=\sum \limits _{n=1}^{\infty }(-1)^{n-1}{\frac {\pi ^{2n-1}}{(2n-1)(2n-1)!}}}$ ${\displaystyle =\pi -{\frac {\pi ^{3}}{3\cdot 3!}}+{\frac {\pi ^{5}}{5\cdot 5!}}-{\frac {\pi ^{7}}{7\cdot 7!}}+\cdots }$	SinIntegral[Pi]		A036792	[1;1,5,1,3,15,1,5,3,2,7,2,1,62,1,3,110,1,39,...]		1.85193705198246617036105337015799136
0.23571113171923293137	ثابت كوبلاند – إيردوس [138]		${\displaystyle {{\mathcal {C}}_{CE}}}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {p_{n}}{10^{n+\sum \limits _{k=1}^{n}\lfloor \log _{10}{p_{k}}\rfloor }}}}$	sum[n=1 to ∞] {prime(n) /(n+(10^ sum[k=1 to n]{floor (log_10 prime(k))}))}	غ.ك	A033308	[0;4,4,8,16,18,5,1,1,1,1,7,1,1,6,2,9,58,1,3,...]		0.23571113171923293137414347535961677
1.523627086202492106277	البعد الكسري لمنحني التنين [139]		${\displaystyle {C_{d}}}$	${\displaystyle {\frac {\log \left({\frac {1+{\sqrt[{3}]{73-6{\sqrt {87}}}}+{\sqrt[{3}]{73+6{\sqrt {87}}}}}{3}}\right)}{\log(2)}}}$	(log((1+(73-6 sqrt(87))^1/3+ (73+6 sqrt(87))^1/3)/3))/ log(2)))	م		[1;1,1,10,12,2,1,149,1,1,1,3,11,1,3,17,4,1,...]		1.52362708620249210627768393595421662
1.78221397819136911177	ثابت جروثينديك[140]		${\displaystyle {K_{R}}}$	${\displaystyle {\frac {\pi }{2\log(1+{\sqrt {2}})}}}$	pi/(2 log(1+sqrt(2)))		A088367	[1;1,3,1,1,2,4,2,1,1,17,1,12,4,3,5,10,1,1,3,...]		1.78221397819136911177441345297254934
1.58496250072115618145	بعد هاوسدورف، مثلث سيربنسكي [141]		${\displaystyle {log_{2}3}}$	${\displaystyle {\frac {\log 3}{\log 2}}={\frac {\sum _{n=0}^{\infty }{\frac {1}{2^{2n+1}(2n+1)}}}{\sum _{n=0}^{\infty }{\frac {1}{3^{2n+1}(2n+1)}}}}={\frac {{\frac {1}{2}}+{\frac {1}{24}}+{\frac {1}{160}}+\cdots }{{\frac {1}{3}}+{\frac {1}{81}}+{\frac {1}{1215}}+\cdots }}}$	( Sum[n=0 to ∞] {1/ (2^(2n+1) (2n+1))})/ (Sum[n=0 to ∞] {1/ (3^(2n+1) (2n+1))})	م	A020857	[1;1,1,2,2,3,1,5,2,23,2,2,1,1,55,1,4,3,1,1,...]		1.58496250072115618145373894394781651
1.30637788386308069	ثابت ميلز [142]		${\displaystyle {\theta }}$	${\displaystyle \lfloor \theta ^{3^{n}}\rfloor }$ primes	Nest[ NextPrime[#^3] &, 2, 7]^(1/3^8)		A051021	[1;3,3,1,3,1,2,1,2,1,4,2,35,21,1,4,4,1,1,3,2,...]	1947	1.30637788386308069046861449260260571
2.02988321281930725004	عقدة الرقم 8 [143]		${\displaystyle {V_{8}}}$	${\displaystyle 2{\sqrt {3}}\,\sum _{n=1}^{\infty }{\frac {1}{n{2n \choose n}}}\sum _{k=n}^{2n-1}{\frac {1}{k}}=6\int \limits _{0}^{\pi /3}\log \left({\frac {1}{2\sin t}}\right)\,dt=}$ ${\displaystyle \scriptstyle {\frac {\sqrt {3}}{9}}\,\sum \limits _{n=0}^{\infty }{\frac {(-1)^{n}}{27^{n}}}\,\left\{\!{\frac {18}{(6n+1)^{2}}}-{\frac {18}{(6n+2)^{2}}}-{\frac {24}{(6n+3)^{2}}}-{\frac {6}{(6n+4)^{2}}}+{\frac {2}{(6n+5)^{2}}}\!\right\}}$	6 integral[0 to pi/3] {log(1/(2 sin (n)))}		A091518	[2;33,2,6,2,1,2,2,5,1,1,7,1,1,1,113,1,4,5,1,...]		2.02988321281930725004240510854904057
262537412640768743.999999999999250073	ثابت هيرميت-رامانوجان [144]		${\displaystyle {R}}$	${\displaystyle e^{\pi {\sqrt {163}}}}$	e^(π sqrt(163))	م	A060295	[262537412640768743;1,1333462407511,1,8,1,1,5,...]	1859	262537412640768743.999999999999250073
1.74540566240734686349	المتوسط التوافقي خنشن [145]		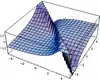${\displaystyle {K_{-1}}}$	${\displaystyle {\frac {\log 2}{\sum \limits _{n=1}^{\infty }{\frac {1}{n}}\log {\bigl (}1{+}{\frac {1}{n(n+2)}}{\bigr )}}}=\lim _{n\to \infty }{\frac {n}{{\frac {1}{a_{1}}}+{\frac {1}{a_{2}}}+\cdots +{\frac {1}{a_{n}}}}}}$ a1 ... an هي عناصر كسر مستمر [a0; a1, a2, ..., an]	(log 2)/ (sum[n=1 to ∞] {1/n log(1+ 1/(n(n+2))}		A087491	[1;1,2,1,12,1,5,1,5,13,2,13,2,1,9,1,6,1,3,1,...]		1.74540566240734686349459630968366106
1.648721270700128146848	الجذر التربيعي للعدد ه[146]		${\displaystyle {\sqrt {e}}}$	${\displaystyle \sum _{n=0}^{\infty }{\frac {1}{2^{n}n!}}=\sum _{n=0}^{\infty }{\frac {1}{(2n)!!}}={\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{8}}+{\frac {1}{48}}+\cdots }$	Sum[n=0 to ∞] {1/(2^n n!)}	م	A019774	[1;1,1,1,5,1,1,9,1,1,13,1,1,17,1,1,21,1,1,...] = [1;1,1,1,4p+1], p∈ℕ		1.64872127070012814684865078781416357
1.017343061984449139714	زيتا(6) [147]		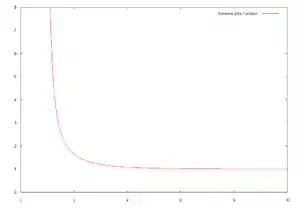${\displaystyle \zeta (6)}$	${\displaystyle {\frac {\pi ^{6}}{945}}\!=\!\prod _{n=1}^{\infty }\!{\underset {p_{n}:{\text{ prime}}}{\frac {1}{{1-p_{n}}^{-6}}}}={\frac {1}{1\!-\!2^{-6}}}\!\cdot \!{\frac {1}{1\!-\!3^{-6}}}\!\cdot \!{\frac {1}{1\!-\!5^{-6}}}\cdots }$	Prod[n=1 to ∞] {1/(1-ithprime (n)^-6)}	م	A013664	[1;57,1,1,1,15,1,6,3,61,1,5,3,1,6,1,3,3,6,1,...]		1.01734306198444913971451792979092052
0.108410151223111361511	ثابت تروت [148]		${\displaystyle \mathrm {T} _{1}}$	${\displaystyle \textstyle [1,0,8,4,1,0,1,5,1,2,2,3,1,1,1,3,6,...]}$ ${\displaystyle {\tfrac {1}{1+{\tfrac {1}{0+{\tfrac {1}{8+{\tfrac {1}{4+{\tfrac {1}{1+{\tfrac {1}{0+1{/\cdots }}}}}}}}}}}}}}$			A039662	[0;9,4,2,5,1,2,2,3,1,1,1,3,6,1,5,1,1,2,...]		0.10841015122311136151129081140641509
0.0078749969978123844	ثابت شاتان [149]		${\displaystyle \Omega }$	${\displaystyle \sum _{p\in P}2^{-|p|}}$		م	A100264	[0; 126, 1, 62, 5, 5, 3, 3, 21, 1, 4, 1]	1975	0.0078749969978123844
0.83462684167407318628	ثابت جاووس نص صغير[150]		${\displaystyle {G}}$	${\displaystyle {\frac {1}{\mathrm {agm} (1,{\sqrt {2}})}}={\frac {4{\sqrt {2}}\,({\tfrac {1}{4}}!)^{2}}{\pi ^{3/2}}}={\frac {2}{\pi }}\int _{0}^{1}{\frac {dx}{\sqrt {1-x^{4}}}}}$	(4 sqrt(2)((1/4)!)^2) /pi^(3/2)	م	A014549	[0;1,5,21,3,4,14,1,1,1,1,1,3,1,15,1,3,7,1,...]		0.83462684167407318628142973279904680
1.451369234883381050283	ثابت سولدنر رامانجن[151][152]		${\displaystyle {\mu }}$	${\displaystyle \mathrm {li} (x)=\int \limits _{0}^{x}{\frac {dt}{\ln t}}=0{\color {White}{......}}}$ li = لوغارتم خطي ${\displaystyle \mathrm {li} (x)\;=\;\mathrm {Ei} (\ln {x}){\color {White}{........}}}$ Ei = تكامل أسي	FindRoot[li(x) = 0]	غ.ك	A070769	[1;2,4,1,1,1,3,1,1,1,2,47,2,4,1,12,1,1,2,2,1,...]	1792 to 1809	1.45136923488338105028396848589202744
0.64341054628833802618	ثابت الكاهن [153]		${\displaystyle \xi _{2}}$	${\displaystyle \sum _{k=1}^{\infty }{\frac {(-1)^{k}}{s_{k}-1}}={\frac {1}{1}}-{\frac {1}{2}}+{\frac {1}{6}}-{\frac {1}{42}}+{\frac {1}{1806}}{\,\pm \cdots }}$ ${\displaystyle \,\,S_{0}=\,2,\,\,S_{k}=\,1+\prod \limits _{n=0}^{k-1}S_{n}{\text{ for}}\;k>0}$		م	A080130	[0; 1, 1, 1, 4, 9, 196, 16641, 639988804, ...]	1891	0.64341054628833802618225430775756476
1.414213562373095048801	الجذر التربيعي ل 2، ثابت فيثاغورس .[154]		${\displaystyle {\sqrt {2}}}$	${\displaystyle \!\prod _{n=1}^{\infty }\!\left(1\!+\!{\frac {(-1)^{n+1}}{2n-1}}\right)\!=\!\left(1\!+\!{\frac {1}{1}}\right)\!\left(1\!-\!{\frac {1}{3}}\right)\!\left(1\!+\!{\frac {1}{5}}\right)\cdots }$	prod[n=1 to ∞] {1+(-1)^(n+1) /(2n-1)}	ج	A002193	[1;2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,...] = [1;2...]		1.41421356237309504880168872420969808
1.77245385090551602729	ثابت كارلسون ليفين [117]		${\displaystyle {\Gamma }({\tfrac {1}{2}})}$	${\displaystyle {\sqrt {\pi }}=\left(-{\frac {1}{2}}\right)!=\int _{-\infty }^{\infty }{\frac {1}{e^{x^{2}}}}\,dx=\int _{0}^{1}{\frac {1}{\sqrt {-\ln x}}}\,dx}$	sqrt (pi)	م	A002161	[1;1,3,2,1,1,6,1,28,13,1,1,2,18,1,1,1,83,1,...]		1.77245385090551602729816748334114518
1.05946309435929526456	الفاصل الموسيقي بين نصف كل نغمة[155][156]		${\displaystyle {\sqrt[{12}]{2}}}$	${\displaystyle {\begin{array}{l|ccccccccccccr}\!2^{\frac {x}{12}}\!&\!\!\scriptstyle {0}&\!\!\!\!\scriptstyle {1}&\!\!\scriptstyle {2}&\!\!\scriptstyle {3}&\!\!\scriptstyle {4}&\scriptstyle {5}&\!\!\scriptstyle {6}&\!\!\scriptstyle {7}&\!\!\scriptstyle {8}&\!\!\scriptstyle {9}&\!\!\scriptstyle {10}&\!\!\scriptstyle {11}&\!\!\scriptstyle {12}\\\hline \!\scriptstyle {\textrm {Key}}\!&\!\scriptstyle {\mathrm {C_{1}} }&\!\!\scriptstyle {\mathrm {C^{\#}} }&\!\!\scriptstyle {\mathrm {D} }&\!\scriptstyle {\mathrm {D^{\#}} }&\!\!\scriptstyle {\mathrm {E} }&\scriptstyle {\mathrm {F} }&\!\scriptstyle {\mathrm {F^{\#}} }&\!\!\scriptstyle {\mathrm {G} }&\!\scriptstyle {\mathrm {G^{\#}} }&\!\!\scriptstyle {\mathrm {A} }&\!\scriptstyle {\mathrm {A^{\#}} }&\!\!\scriptstyle {\mathrm {B} }&\!\scriptstyle {\mathrm {C_{2}} }\end{array}}}$(A = 440 Hz)	2^(1/12)	ج	A010774	[1;16,1,4,2,7,1,1,2,2,7,4,1,2,1,60,1,3,1,2,...]		1.05946309435929526456182529494634170
1.01494160640965362502	ثابت جيسكنج [157]		${\displaystyle {\pi \ln \beta }}$	${\displaystyle {\frac {3{\sqrt {3}}}{4}}\left(1-\sum _{n=0}^{\infty }{\frac {1}{(3n+2)^{2}}}+\sum _{n=1}^{\infty }{\frac {1}{(3n+1)^{2}}}\right)=}$ ${\displaystyle \textstyle {\frac {3{\sqrt {3}}}{4}}\left(1-{\frac {1}{2^{2}}}+{\frac {1}{4^{2}}}-{\frac {1}{5^{2}}}+{\frac {1}{7^{2}}}-{\frac {1}{8^{2}}}+{\frac {1}{10^{2}}}\pm \cdots \right)}$.	sqrt(3)*3/4 *(1 -Sum[n=0 to ∞] {1/((3n+2)^2)} +Sum[n=1 to ∞] {1/((3n+1)^2)})		A143298	[1;66,1,12,1,2,1,4,2,1,3,3,1,4,1,56,2,2,11,...]	1912	1.01494160640965362502120255427452028
2.62205755429211981046	ثابت ليمنيسكاتي [158]		${\displaystyle {\varpi }}$	${\displaystyle \pi \,{G}=4{\sqrt {\tfrac {2}{\pi }}}\,\Gamma {\left({\tfrac {5}{4}}\right)^{2}}={\tfrac {1}{4}}{\sqrt {\tfrac {2}{\pi }}}\,\Gamma {\left({\tfrac {1}{4}}\right)^{2}}=4{\sqrt {\tfrac {2}{\pi }}}\left({\tfrac {1}{4}}!\right)^{2}}$	4 sqrt(2/pi) ((1/4)!)^2	م	A062539	[2;1,1,1,1,1,4,1,2,5,1,1,1,14,9,2,6,2,9,4,1,...]	1798	2.62205755429211981046483958989111941
1.28242712910062263687	ثابت جلايشر كين كيلن		${\displaystyle {A}}$	${\displaystyle e^{{\frac {1}{12}}-\zeta ^{\prime }(-1)}=e^{{\frac {1}{8}}-{\frac {1}{2}}\sum \limits _{n=0}^{\infty }{\frac {1}{n+1}}\sum \limits _{k=0}^{n}\left(-1\right)^{k}{\binom {n}{k}}\left(k+1\right)^{2}\ln(k+1)}}$	e^(1/12-zeta´{-1})	م	A074962	[1;3,1,1,5,1,1,1,3,12,4,1,271,1,1,2,7,1,35,...]		1.28242712910062263687534256886979172
4.227453533376265408-	دالة دي جاما (1/4) [159]		${\displaystyle {\psi }({\tfrac {1}{4}})}$	${\displaystyle -\gamma -{\frac {\pi }{2}}-3\ln {2}=-\gamma +\sum _{n=0}^{\infty }\left({\frac {1}{n+1}}-{\frac {1}{n+{\tfrac {1}{4}}}}\right)}$	-EulerGamma -\pi/2 -3 log 2		A020777	-[4;4,2,1,1,10,1,5,9,11,1,22,1,1,14,1,2,1,4,...]		-4.2274535333762654080895301460966835
0.286747428434478734107	ثابت الإهمال القوي[160]		${\displaystyle K_{2}}$	${\displaystyle \prod _{n=1}^{\infty }{\underset {p_{n}:{\text{ prime}}}{\left(1-{\frac {3p_{n}-2}{{p_{n}}^{3}}}\right)}}={\frac {6}{\pi ^{2}}}\prod _{n=1}^{\infty }{\underset {p_{n}:{\text{ prime}}}{\left(1-{\frac {1}{p_{n}(p_{n}+1)}}\right)}}}$	N[ prod[k=1 to ∞] {1-(3*prime(k)-2) /(prime(k)^3)}]		A065473	[0;3,2,19,3,12,1,5,1,5,1,5,2,1,1,1,1,1,3,7,...]		0.28674742843447873410789271278983845
3.62560990822190831193	جاما(1/4)[161]		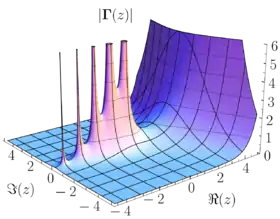${\displaystyle \Gamma ({\tfrac {1}{4}})}$	${\displaystyle 4\left({\frac {1}{4}}\right)!=\left(-{\frac {3}{4}}\right)!}$	4(1/4)!	م	A068466	[3;1,1,1,2,25,4,9,1,1,8,4,1,6,1,1,19,1,1,4,1,...]	1729	3.62560990822190831193068515586767200
1.66168794963359412129	ثابت سموس [162]		${\displaystyle {\sigma }}$	${\displaystyle \prod _{n=1}^{\infty }n^{{1/2}^{n}}={\sqrt {1{\sqrt {2{\sqrt {3\cdots }}}}}}=1^{1/2}\;2^{1/4}\;3^{1/8}\cdots }$	prod[n=1 to ∞] {n ^(1/2)^n}	م	A065481	[1;1,1,1,21,1,1,1,6,4,2,1,1,2,1,3,1,13,13,...]		1.66168794963359412129581892274995074
0.955316618124509278163	الزاوية السحرية [163]		${\displaystyle {\theta _{m}}}$	${\displaystyle \arctan \left({\sqrt {2}}\right)=\arccos \left({\sqrt {\tfrac {1}{3}}}\right)\approx \textstyle {54.7356}^{\circ }}$	arctan(sqrt(2))	م	A195696	[0;1,21,2,1,1,1,2,1,2,2,4,1,2,9,1,2,1,1,1,3,...]		0.95531661812450927816385710251575775
1.78107241799019798523	دالة بارنس [164]		${\displaystyle e^{\gamma }}$	${\displaystyle \prod _{n=1}^{\infty }{\frac {e^{\frac {1}{n}}}{1+{\tfrac {1}{n}}}}=\prod _{n=0}^{\infty }\left(\prod _{k=0}^{n}(k+1)^{(-1)^{k+1}{n \choose k}}\right)^{\frac {1}{n+1}}=}$ ${\displaystyle \textstyle \left({\frac {2}{1}}\right)^{1/2}\left({\frac {2^{2}}{1\cdot 3}}\right)^{1/3}\left({\frac {2^{3}\cdot 4}{1\cdot 3^{3}}}\right)^{1/4}\left({\frac {2^{4}\cdot 4^{4}}{1\cdot 3^{6}\cdot 5}}\right)^{1/5}\cdots }$	Prod[n=1 to ∞] {e^(1/n)} /{1 + 1/n}		A073004	[1;1,3,1,1,3,5,4,1,1,2,2,1,7,9,1,16,1,1,1,2,...]		1.78107241799019798523650410310717954
0.74759792025341143517	ثابت رينيه لركن السيارات [165]		${\displaystyle {m}}$	${\displaystyle \int \limits _{0}^{\infty }exp\left(\!-2\int \limits _{0}^{x}{\frac {1-e^{-y}}{y}}dy\right)\!dx={e^{-2\gamma }}\int \limits _{0}^{\infty }{\frac {e^{-2\Gamma (0,n)}}{n^{2}}}}$	[e^(-2*Gamma)] * Int{n,0,∞}[ e^(- 2 *Gamma(0,n)) /n^2]		A050996	[0;1,2,1,25,3,1,2,1,1,12,1,2,1,1,3,1,2,1,43,...]		0.74759792025341143517873094383017817
1.273239544735162686151	سلسلة رامانوجان-فورسيث [166]		${\displaystyle {\frac {4}{\pi }}}$	${\displaystyle \displaystyle \sum \limits _{n=0}^{\infty }\textstyle \left({\frac {(2n-3)!!}{(2n)!!}}\right)^{2}={1\!+\!\left({\frac {1}{2}}\right)^{2}\!+\!\left({\frac {1}{2\cdot 4}}\right)^{2}\!+\!\left({\frac {1\cdot 3}{2\cdot 4\cdot 6}}\right)^{2}+\cdots }}$	Sum[n=0 to ∞] {[(2n-3)!! /(2n)!!]^2}	غ.ك	A088538	[1;3,1,1,1,15,2,72,1,9,1,17,1,2,1,5,1,1,10,...]		1.27323954473516268615107010698011489
1.444667861009766133658	عدد ستينر، ه جذر ه [167]		${\displaystyle {\sqrt[{e}]{e}}}$	${\displaystyle e^{\frac {1}{e}}{\color {White}{...........}}}$	e^(1/e)	م	A073229	[1;2,4,55,27,1,1,16,9,3,2,8,3,2,1,1,4,1,9,...]		1.44466786100976613365833910859643022
0.692200627555346353865	الحد الأدنى للدالة ƒ(x) = xx [168]		${\displaystyle {\left({\frac {1}{e}}\right)}^{\frac {1}{e}}}$	${\displaystyle {e}^{-{\frac {1}{e}}}{\color {White}{..........}}}$ = مقلوب عدد ستينر	e^(-1/e)		A072364	[0;1,2,4,55,27,1,1,16,9,3,2,8,3,2,1,1,4,1,9,...]		0.69220062755534635386542199718278976
0.34053732955099914282	ثابت السير العشوائي [169]		${\displaystyle {p(3)}}$	${\displaystyle 1-\!\!\left({3 \over (2\pi )^{3}}\int \limits _{-\pi }^{\pi }\int \limits _{-\pi }^{\pi }\int \limits _{-\pi }^{\pi }{dx\,dy\,dz \over 3-\!\cos x-\!\cos y-\!\cos z}\right)^{\!-1}}$ ${\displaystyle =1-16{\sqrt {\tfrac {2}{3}}}\;\pi ^{3}\left(\Gamma ({\tfrac {1}{24}})\Gamma ({\tfrac {5}{24}})\Gamma ({\tfrac {7}{24}})\Gamma ({\tfrac {11}{24}})\right)^{-1}}$	1-16*Sqrt[2/3]*Pi^3 /(Gamma[1/24] *Gamma[5/24] *Gamma[7/24] *Gamma[11/24])		A086230	[0;2,1,14,1,3,8,1,5,2,7,1,12,1,5,59,1,1,1,3,...]		0.34053732955099914282627318443290289
0.543258965342976706952	نظرية بلوتش (المتغيرات المركبة) [170]		${\displaystyle {L}}$	${\displaystyle ={\frac {\Gamma ({\tfrac {1}{3}})\;\Gamma ({\tfrac {5}{6}})}{\Gamma ({\tfrac {1}{6}})}}={\frac {(-{\tfrac {2}{3}})!\;(-1+{\tfrac {5}{6}})!}{(-1+{\tfrac {1}{6}})!}}}$	gamma(1/3) *gamma(5/6) /gamma(1/6)		A081760	[0;1,1,5,3,1,1,2,1,1,6,3,1,8,11,2,1,1,27,4,...]	1929	0.54325896534297670695272829530061323
0.187859642462067120248	ثابت إم أر بي (مارفن راي بيرنز) [171][172][173]		${\displaystyle C_{{}_{MRB}}}$	${\displaystyle \sum _{n=1}^{\infty }(-1)^{n}(n^{1/n}-1)=-{\sqrt[{1}]{1}}+{\sqrt[{2}]{2}}-{\sqrt[{3}]{3}}+\cdots }$	Sum[n=1 to ∞] {(-1)^n (n^(1/n)-1)}		A037077	[0;5,3,10,1,1,4,1,1,1,1,9,1,1,12,2,17,2,2,1,...]	1999	0.18785964246206712024851793405427323
1.4670780794339754728977	ثابت بورتر[174]		${\displaystyle {C}}$	${\displaystyle {\frac {6\ln 2}{\pi ^{2}}}\left(3\ln 2+4\,\gamma -{\frac {24}{\pi ^{2}}}\,\zeta '(2)-2\right)-{\frac {1}{2}}}$ ${\displaystyle \scriptstyle \gamma \,{\text{= Euler–Mascheroni Constant}}=0.5772156649\ldots }$ ${\displaystyle \scriptstyle \zeta '(2)\,{\text{= Derivative of }}\zeta (2)=-\sum \limits _{n=2}^{\infty }{\frac {\ln n}{n^{2}}}=-0.9375482543\ldots }$	6*ln2/pi^2(3*ln2+ 4 EulerGamma- WeierstrassZeta'(2) *24/pi^2-2)-1/2		A086237	[1;2,7,10,1,2,38,5,4,1,4,12,5,1,5,1,2,3,1,...]	1974	1.46707807943397547289779848470722995
4.66920160910299067185	ثابت فايينبوم δ [175]		${\displaystyle {\delta }}$	${\displaystyle \lim _{n\to \infty }{\frac {x_{n+1}-x_{n}}{x_{n+2}-x_{n+1}}}\qquad \scriptstyle x\in (3.8284;\,3.8495)}$ ${\displaystyle \scriptstyle x_{n+1}=\,ax_{n}(1-x_{n})\quad {\text{or}}\quad x_{n+1}=\,a\sin(x_{n})}$		م	A006890	[4;1,2,43,2,163,2,3,1,1,2,5,1,2,3,80,2,5,...]	1975	4.66920160910299067185320382046620161
2.50290787509589282228	ثابت فايينبوم α[176]		${\displaystyle \alpha }$	${\displaystyle \lim _{n\to \infty }{\frac {d_{n}}{d_{n+1}}}}$		م	A006891	[2;1,1,85,2,8,1,10,16,3,8,9,2,1,40,1,2,3,...]	1979	2.50290787509589282228390287321821578
0.62432998854355087099	ثابت غولومب-ديكمان [177]		${\displaystyle {\lambda }}$	${\displaystyle \int \limits _{0}^{\infty }{\underset {{\text{Para }}x>2}{{\frac {f(x)}{x^{2}}}\,dx}}=\int \limits _{0}^{1}e^{\operatorname {Li} (n)}dn\quad \scriptstyle {\text{Li: Logarithmic integral}}}$	N[Int{n,0,1}[e^Li(n)],34]		A084945	[0;1,1,1,1,1,22,1,2,3,1,1,11,1,1,2,22,2,6,1,...]	1930 & 1964	0.62432998854355087099293638310083724
23.1406926327792690057	ثابت غيلفوند [178]		${\displaystyle {e}^{\pi }}$	${\displaystyle (-1)^{-i}=i^{-2i}=\sum _{n=0}^{\infty }{\frac {\pi ^{n}}{n!}}={\frac {\pi ^{1}}{1}}+{\frac {\pi ^{2}}{2!}}+{\frac {\pi ^{3}}{3!}}+\cdots }$	Sum[n=0 to ∞] {(pi^n)/n!}	م	A039661	[23;7,9,3,1,1,591,2,9,1,2,34,1,16,1,30,1,...]		23.1406926327792690057290863679485474
7.38905609893065022723	الثابت المخروطى، ثابت شوارتزشيلد [179]		${\displaystyle e^{2}}$	${\displaystyle \sum _{n=0}^{\infty }{\frac {2^{n}}{n!}}=1+2+{\frac {2^{2}}{2!}}+{\frac {2^{3}}{3!}}+{\frac {2^{4}}{4!}}+{\frac {2^{5}}{5!}}+\cdots }$	Sum[n=0 to ∞] {2^n/n!}	م	A072334	[7;2,1,1,3,18,5,1,1,6,30,8,1,1,9,42,11,1,...] = [7,2,1,1,n,4*n+6,n+2], n = 3, 6, 9, etc.		7.38905609893065022723042746057500781
0.35323637185499598454	ثابت هافنر – سارنك – مككورليي (1) [180]		${\displaystyle {\sigma }}$	${\displaystyle \prod _{k=1}^{\infty }\left\{1-[1-\prod _{j=1}^{n}{\underset {p_{k}:{\text{ prime}}}{(1-p_{k}^{-j})]^{2}}}\right\}}$	prod[k=1 to ∞] {1-(1-prod[j=1 to n] {1-ithprime(k)^-j})^2}		A085849	[0;2,1,4,1,10,1,8,1,4,1,2,1,2,1,2,6,1,1,1,3,...]	1993	0.35323637185499598454351655043268201
0.60792710185402662866	ثابت هافنر – سارنك – مككورليي (2) [181]		${\displaystyle {\frac {1}{\zeta (2)}}}$	${\displaystyle {\frac {6}{\pi ^{2}}}=\prod _{n=0}^{\infty }{\underset {p_{n}:{\text{ prime}}}{\!\left(\!1-{\frac {1}{{p_{n}}^{2}}}\!\right)}}\!=\!\textstyle \left(1\!-\!{\frac {1}{2^{2}}}\right)\!\left(1\!-\!{\frac {1}{3^{2}}}\right)\!\left(1\!-\!{\frac {1}{5^{2}}}\right)\cdots }$	Prod{n=1 to ∞} (1-1/ithprime(n)^2)	م	A059956	[0;1,1,1,1,4,2,4,7,1,4,2,3,4,10,1,2,1,1,1,...]		0.60792710185402662866327677925836583
0.12345678910111213141	ثابت تشامبيرنوون [182]		${\displaystyle C_{10}}$	${\displaystyle \sum _{n=1}^{\infty }\;\sum _{k=10^{n-1}}^{10^{n}-1}{\frac {k}{10^{kn-9\sum _{j=0}^{n-1}10^{j}(n-j-1)}}}}$		م	A033307	[0;8,9,1,149083,1,1,1,4,1,1,1,3,4,1,1,1,15,...]	1933	0.12345678910111213141516171819202123
0.76422365358922066299	ثابت رامانجن-لاندو [183]		${\displaystyle K}$	${\displaystyle {\frac {1}{\sqrt {2}}}\prod _{p\equiv 3\!\!\!\!\!\mod \!4}\!\!{\underset {\!\!\!\!\!\!\!\!p:{\text{ prime}}}{\left(1-{\frac {1}{p^{2}}}\right)^{-{\frac {1}{2}}}}}\!\!={\frac {\pi }{4}}\prod _{p\equiv 1\!\!\!\!\!\mod \!4}\!\!{\underset {\!\!\!\!p:{\text{ prime}}}{\left(1-{\frac {1}{p^{2}}}\right)^{\frac {1}{2}}}}}$		م	A064533	[0;1,3,4,6,1,15,1,2,2,3,1,23,3,1,1,3,1,1,6,4,...]		0.76422365358922066299069873125009232
2.71828182845904523536	العدد ه، العدد النيبيري، عدد أويلر [184]		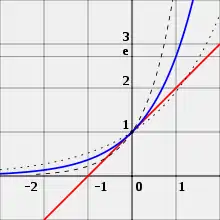${\displaystyle {e}}$	${\displaystyle \!\lim _{n\to \infty }\!\left(\!1\!+\!{\frac {1}{n}}\right)^{n}\!=\!\sum _{n=0}^{\infty }{\frac {1}{n!}}={\frac {1}{0!}}+{\frac {1}{1}}+{\frac {1}{2!}}+{\frac {1}{3!}}+\textstyle \cdots }$	Sum[n=0 to ∞] {1/n!} (* lim_(n->∞) (1+1/n)^n *)	م	A001113	[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,...] = [2;1,2p,1], p∈ℕ		2.71828182845904523536028747135266250
0.3678794411714423215955	معكوس العدد ه، معكوس العدد النيبيري، معكوس عدد أويلر [185]		${\displaystyle {\frac {1}{e}}}$	${\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{n!}}={\frac {1}{0!}}-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+{\frac {1}{4!}}-{\frac {1}{5!}}+\cdots }$	Sum[n=2 to ∞] {(-1)^n/n!}	م	A068985	[0;2,1,1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,...] = [0;2,1,1,2p,1], p∈ℕ	1618	0.36787944117144232159552377016146086
0.69034712611496431946	الحد الأعلى للدالة الأسية المكررة[186]		${\displaystyle {H}_{2n+1}}$	${\displaystyle \lim _{n\to \infty }{H}_{2n+1}=\textstyle \left({\frac {1}{2}}\right)^{\left({\frac {1}{3}}\right)^{\left({\frac {1}{4}}\right)^{\cdot ^{\cdot ^{\left({\frac {1}{2n+1}}\right)}}}}}={2}^{-3^{-4^{\cdot ^{\cdot ^{-2n-1}}}}}}$	2^-3^-4^-5^-6^ -7^-8^-9^-10^ -11^-12^-13 …		A242760	[0;1,2,4,2,1,3,1,2,2,1,4,1,2,4,3,1,1,10,1,3,2,...]		0.69034712611496431946732843846418942
0.6583655992	الحد الأدنى للدالة الأسية المكررة [187]		${\displaystyle {H}_{2n}}$	${\displaystyle \lim _{n\to \infty }{H}_{2n}=\textstyle \left({\frac {1}{2}}\right)^{\left({\frac {1}{3}}\right)^{\left({\frac {1}{4}}\right)^{\cdot ^{\cdot ^{\left({\frac {1}{2n}}\right)}}}}}={2}^{-3^{-4^{\cdot ^{\cdot ^{-2n}}}}}}$	2^-3^-4^-5^-6^ -7^-8^-9^-10^ -11^-12 …			[0;1,1,1,12,1,2,1,1,4,3,1,1,2,1,2,1,51,2,2,1,...]		0.6583655992.
3.14159265358979323846264	ط، ثابت أرخميدس، ثابت الدائرة، باي [188]		${\displaystyle \pi }$	${\displaystyle \lim _{n\to \infty }\,2^{n}\underbrace {\sqrt {2-{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}} _{n}}$	Sum[n=0 to ∞] {(-1)^n 4/(2n+1)}	م	A000796	[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,...]		3.14159265358979323846264338327950288
1.9287800	ثابت رايت [189]		${\displaystyle {\omega }}$	${\displaystyle \left\lfloor 2^{2^{2^{\cdot ^{\cdot ^{2^{\omega }}}}}}\!\right\rfloor \scriptstyle {\text{= primes:}}\displaystyle \left\lfloor 2^{\omega }\right\rfloor \scriptstyle {\text{=3,}}\displaystyle \left\lfloor 2^{2^{\omega }}\right\rfloor \scriptstyle {\text{=13,}}\displaystyle \left\lfloor 2^{2^{2^{\omega }}}\right\rfloor \scriptstyle =16381,\ldots }$			A086238	[1; 1, 13, 24, 2, 1, 1, 3, 1, 1, 3]		1.9287800
0.4636476090008061162142	سلسلة ماشين-غريغوري[190]		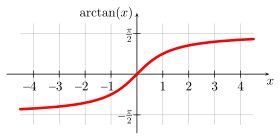${\displaystyle \arctan {\frac {1}{2}}}$	${\displaystyle {\underset {{\text{For }}x=1/2\qquad \qquad }{\sum _{n=0}^{\infty }{\frac {(\!-1\!)^{n}\,x^{2n+1}}{2n+1}}={\frac {1}{2}}{-}{\frac {1}{3\!\cdot \!2^{3}}}{+}{\frac {1}{5\!\cdot \!2^{5}}}{-}{\frac {1}{7\!\cdot \!2^{7}}}{+}\cdots }}}$	Sum[n=0 to ∞] {(-1)^n (1/2)^(2n+1) /(2n+1)}	غ.ك	A073000	[0;2,6,2,1,1,1,6,1,2,1,1,2,10,1,2,1,2,1,1,1,...]		0.46364760900080611621425623146121440
0.6977746579640079820067	ثابت الكسر المستمر، دالة بيسل[191]		${\displaystyle {C}_{CF}}$	${\displaystyle {\frac {I_{1}(2)}{I_{0}(2)}}={\frac {\sum \limits _{n=0}^{\infty }{\frac {n}{n!n!}}}{\sum \limits _{n=0}^{\infty }{\frac {1}{n!n!}}}}=\textstyle {\tfrac {1}{1+{\tfrac {1}{2+{\tfrac {1}{3+{\tfrac {1}{4+{\tfrac {1}{5+{\tfrac {1}{6+1{/\cdots }}}}}}}}}}}}}}$	(Sum [n=0 to ∞] {n/(n!n!)}) / (Sum [n=0 to ∞] {1/(n!n!)})	غ.ك	A052119	[0;1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,...] = [0;p+1], p∈ℕ		0.69777465796400798200679059255175260
1.902160583104	مبرهنة برون = Σ مجموع مقلوب الأعداد الأولية التوأم [192]		${\displaystyle {B}_{\,2}}$	${\displaystyle \textstyle {\underset {p,\,p+2:{\text{ prime}}}{\sum ({\frac {1}{p}}+{\frac {1}{p+2}})}}=({\frac {1}{3}}\!+\!{\frac {1}{5}})+({\tfrac {1}{5}}\!+\!{\tfrac {1}{7}})+({\tfrac {1}{11}}\!+\!{\tfrac {1}{13}})+\cdots }$			A065421	[1; 1, 9, 4, 1, 1, 8, 3, 4, 4, 2, 2]		1.902160583104
0.870588379975	مبرهنة برون = Σ مجموع مقلوب مجموعة التوأم الرباعي [193]		${\displaystyle {B}_{\,4}}$	${\displaystyle \textstyle {\sum ({\frac {1}{p}}+{\frac {1}{p+2}}+{\frac {1}{p+6}}+{\frac {1}{p+8}})}\scriptstyle \quad {p,\;p+2,\;p+6,\;p+8:{\text{ prime}}}}$ ${\displaystyle \textstyle {\left({\tfrac {1}{5}}+{\tfrac {1}{7}}+{\tfrac {1}{11}}+{\tfrac {1}{13}}\right)}+\left({\tfrac {1}{11}}+{\tfrac {1}{13}}+{\tfrac {1}{17}}+{\tfrac {1}{19}}\right)+\dots }$			A213007	[0; 1, 6, 1, 2, 1, 2, 956, 3, 1, 1]		0.870588379975
0.63661977236758134307	ثابت بوفون[194]		${\displaystyle {\frac {2}{\pi }}}$	${\displaystyle {\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2}}}}{2}}\cdot {\frac {\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}{2}}\cdots }$ صيغة فييت	2/Pi	م	A060294	[0;1,1,1,3,31,1,145,1,4,2,8,1,6,1,2,3,1,4,...]	1540 to 1603	0.63661977236758134307553505349005745
0.59634736232319407434	ثابت جومبرتز [195]		${\displaystyle {G}}$	${\displaystyle \!\int \limits _{0}^{\infty }\!\!{\frac {e^{-n}}{1{+}n}}\,dn=\!\!\int \limits _{0}^{1}\!\!{\frac {1}{1{-}\ln n}}\,dn=\textstyle {\tfrac {1}{1+{\tfrac {1}{1+{\tfrac {1}{1+{\tfrac {2}{1+{\tfrac {2}{1+{\tfrac {3}{1+3{/\cdots }}}}}}}}}}}}}}$	integral[0 to ∞] {(e^-n)/(1+n)}	غ.ك	A073003	[0;1,1,2,10,1,1,4,2,2,13,2,4,1,32,4,8,1,1,1,...]		0.59634736232319407434107849936927937
ت	وحدة تخيلية [196]		${\displaystyle {i}}$	${\displaystyle {\sqrt {-1}}={\frac {\ln(-1)}{\pi }}\qquad \qquad \mathrm {e} ^{i\,\pi }=-1}$	sqrt(-1)	غ.ك، خ			1501 to 1576	i
2.74723 82749 32304 33305	ثابت رامانجن للمتداخلة الجذرية [197]		${\displaystyle R_{5}}$	${\displaystyle \scriptstyle {\sqrt {5+{\sqrt {5+{\sqrt {5-{\sqrt {5+{\sqrt {5+{\sqrt {5+{\sqrt {5-\cdots }}}}}}}}}}}}}}\;=\textstyle {\frac {2+{\sqrt {5}}+{\sqrt {15-6{\sqrt {5}}}}}{2}}}$	(2+sqrt(5) +sqrt(15 -6 sqrt(5)))/2	ج		[2;1,2,1,21,1,7,2,1,1,2,1,2,1,17,4,4,1,1,4,2,...]		2.74723827493230433305746518613420282
0.56714 32904 09783 87299	ثابت أوميجا [198]		${\displaystyle {\Omega }}$	${\displaystyle \sum _{n=1}^{\infty }{\frac {(-n)^{n-1}}{n!}}=\,\left({\frac {1}{e}}\right)^{\left({\frac {1}{e}}\right)^{\cdot ^{\cdot ^{\left({\frac {1}{e}}\right)}}}}=e^{-\Omega }=e^{-e^{-e^{\cdot ^{\cdot ^{-e}}}}}}$	Sum[n=1 to ∞] {(-n)^(n-1)/n!}	م	A030178	[0;1,1,3,4,2,10,4,1,1,1,1,2,7,306,1,5,1,2,1,...]		0.56714329040978387299996866221035555
0.968946146259369380483	بيتا(3) [199]		${\displaystyle {\beta }(3)}$	${\displaystyle {\frac {\pi ^{3}}{32}}=\sum _{n=1}^{\infty }{\frac {-1^{n+1}}{(-1+2n)^{3}}}={\frac {1}{1^{3}}}{-}{\frac {1}{3^{3}}}{+}{\frac {1}{5^{3}}}{-}{\frac {1}{7^{3}}}{+}\cdots }$	Sum[n=1 to ∞] {(-1)^(n+1) /(-1+2n)^3}	م	A153071	[0;1,31,4,1,18,21,1,1,2,1,2,1,3,6,3,28,1,...]		0.96894614625936938048363484584691860
2.236067977499789696409	الجذر التربيعي ل 5، مجموع غاوس [200]		${\displaystyle {\sqrt {5}}}$	${\displaystyle \scriptstyle (n=5)\displaystyle \sum _{k=0}^{n-1}e^{\frac {2k^{2}\pi i}{n}}=1+e^{\frac {2\pi i}{5}}+e^{\frac {8\pi i}{5}}+e^{\frac {18\pi i}{5}}+e^{\frac {32\pi i}{5}}}$	Sum[k=0 to 4] {e^(2k^2 pi i/5)}	ج	A002163	[2;4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,...] = [2;4,...]		2.23606797749978969640917366873127624
3.35988566624317755317	ثابت فيبوناتشي[201]		${\displaystyle \Psi }$	${\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{n}}}={\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{8}}+{\frac {1}{13}}+\cdots }$ Fn: متتالية فيبوناتشي	Sum[n=1 to ∞] {1/Fibonacci[n]}	غ.ك	A079586	[3;2,1,3,1,1,13,2,3,3,2,1,1,6,3,2,4,362,...]		3.35988566624317755317201130291892717
2.685452001065306445309	ثابت خينتشين [202]		${\displaystyle K_{\,0}}$	${\displaystyle \prod _{n=1}^{\infty }\left[{1+{1 \over n(n+2)}}\right]^{\ln n/\ln 2}}$	Prod[n=1 to ∞] {(1+1/(n(n+2))) ^(ln(n)/ln(2))}	م	A002210	[2;1,2,5,1,1,2,1,1,3,10,2,1,3,2,24,1,3,2,...]	1934	2.68545200106530644530971483548179569